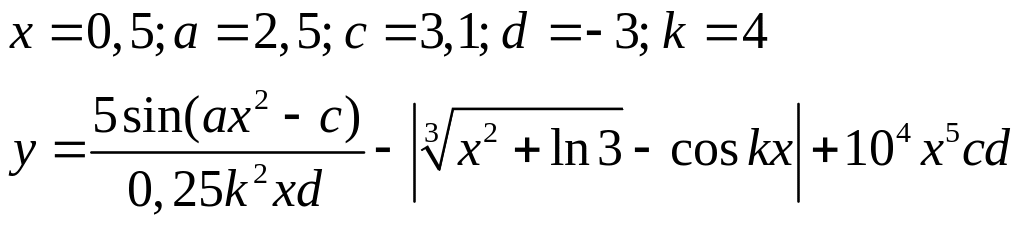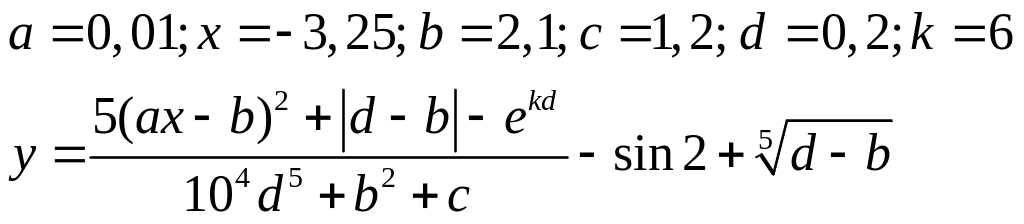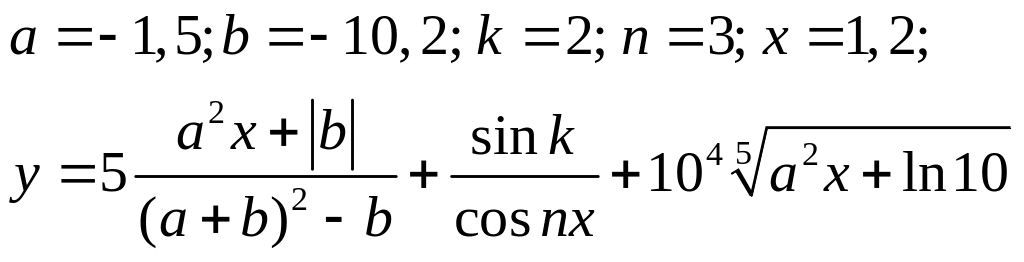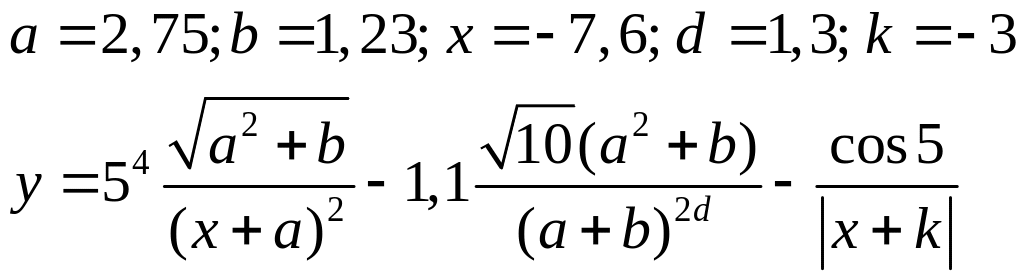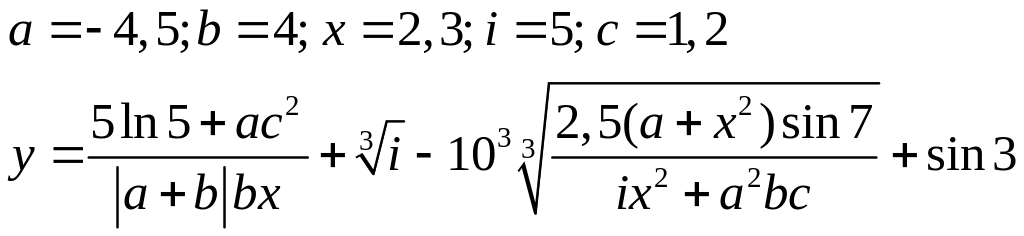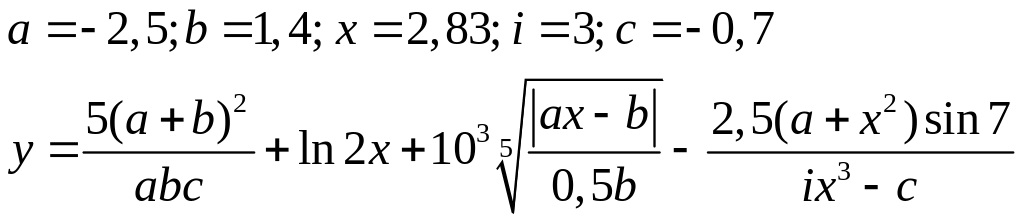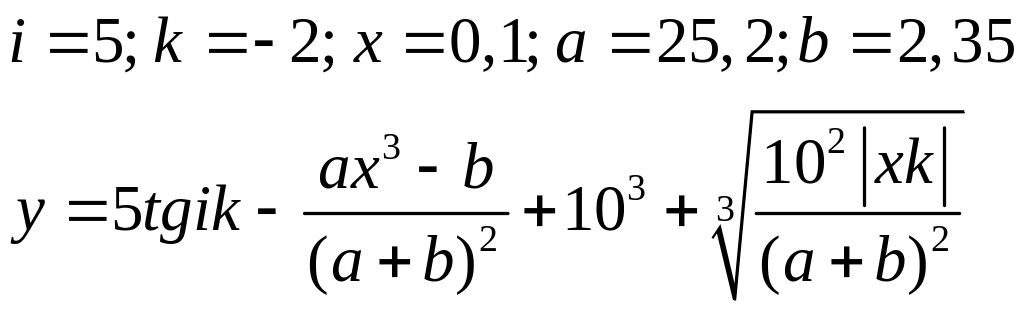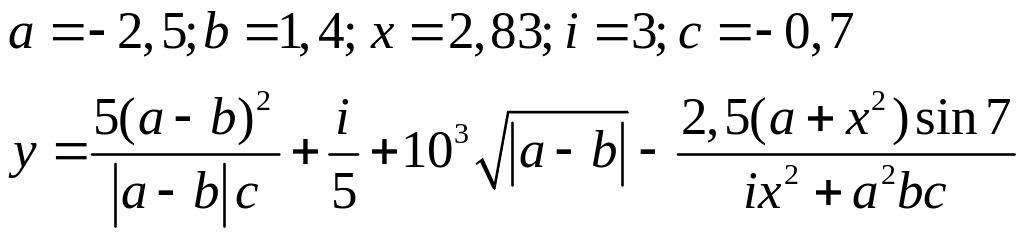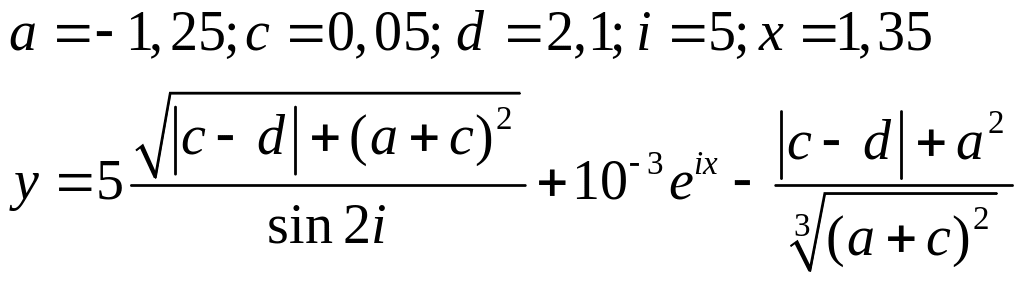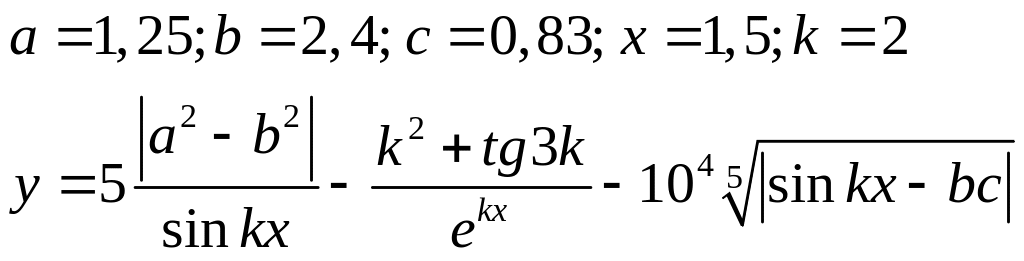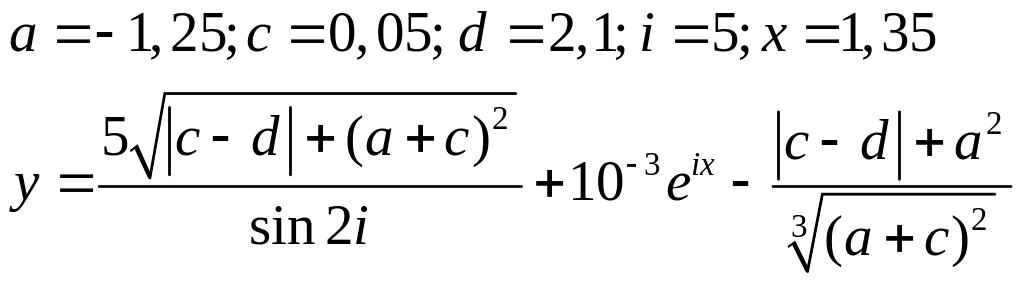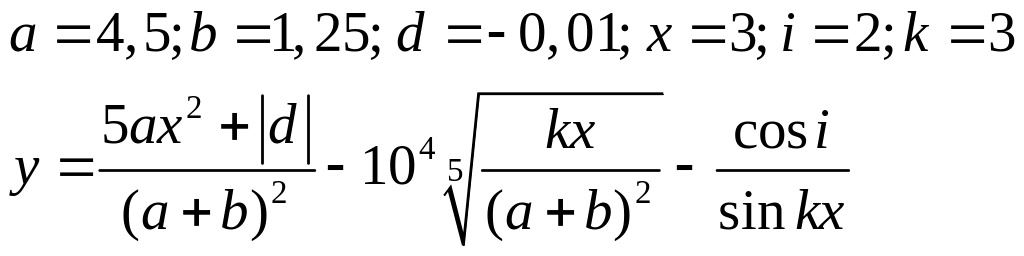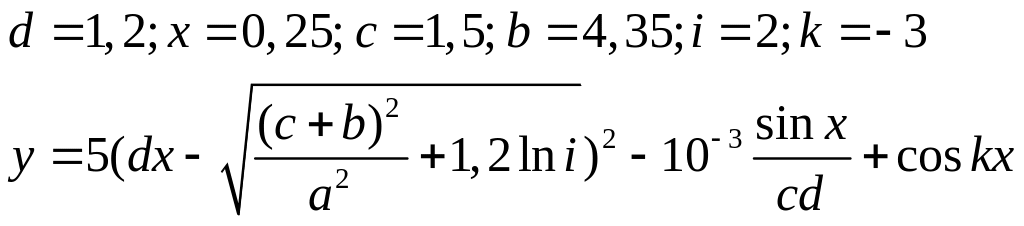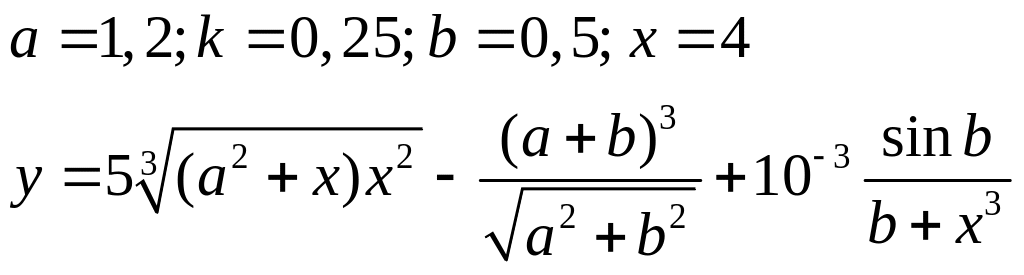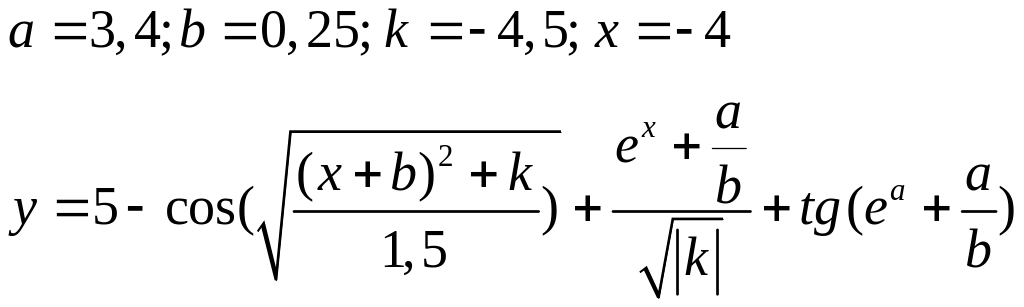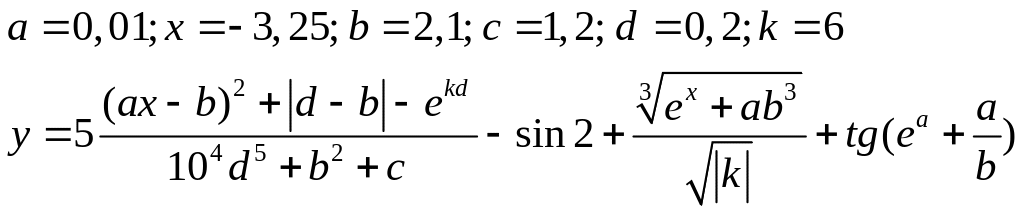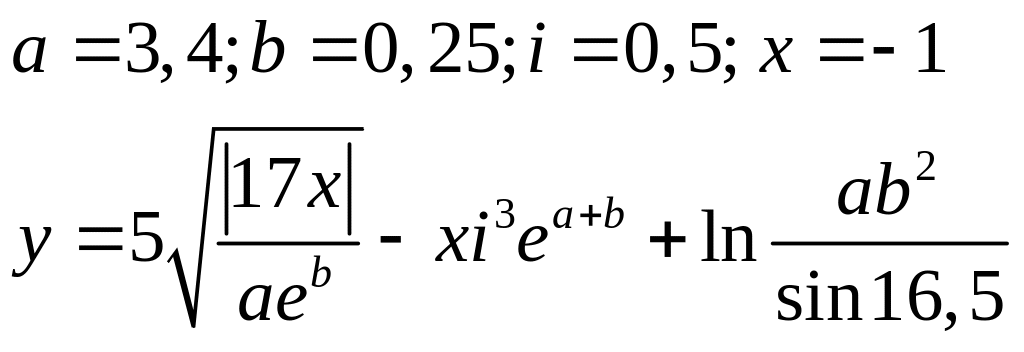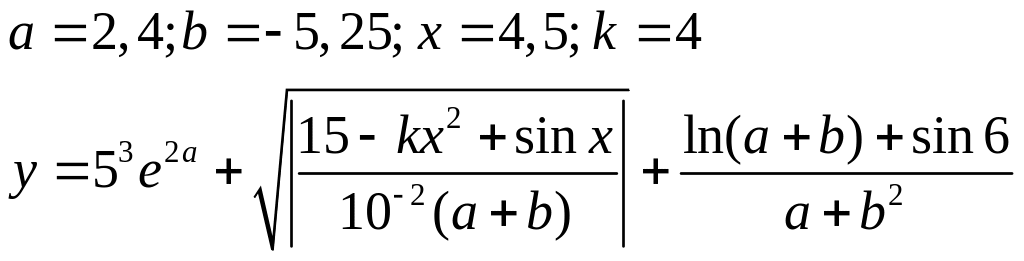Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5108 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Полтавский национальный технический университет им. Ю. Кондратюка
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
РГР3 2013 ПСМС.doc
Скачиваний:
0
Добавлен:
01.05.2025
Размер:
478.72 Кб
Скачать
☆
►Содержание►

Розрахунково-графічна робота з дисципліни “Програмні середовища моделювання систем”

Завдання 1.

1. Побудова двовимірних та тривимірних графіків у різних підвікнах.

3. Створення графічного інтерфейсу користувача.

3.1 Доповнити створену програму вікном, що містить кнопку для побудови графіка.

3.2 Створити додатковий елемент керування (прапорець або список, що випадає) для вибору двовимірної / тривимірної графіки.

Завдання 2.

  1. Побудувати двовимірні графіки згідно варіанту.

  2. Побудувати мембрану – логотип MATLAB (MEMBRANE). Графік підписати таким чином: мембрана. Копію графіка розвернути під довільним кутом.

  3. Побудувати стовпчасті діаграми згідно варіанту (функція BAR).

  4. Побудувати лінії рівня функції 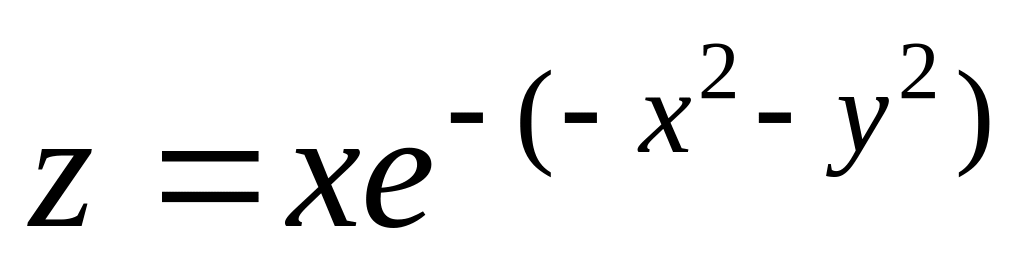в області 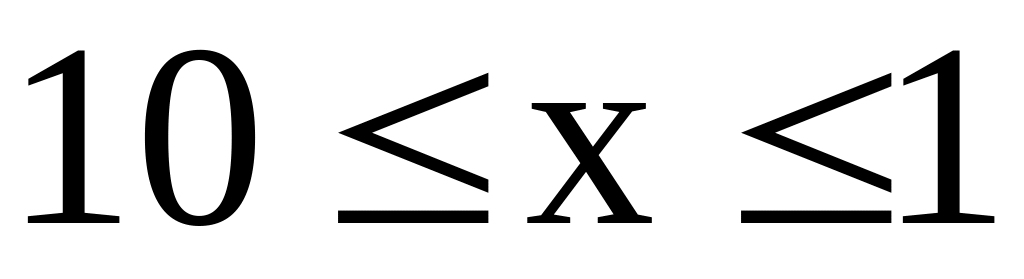, 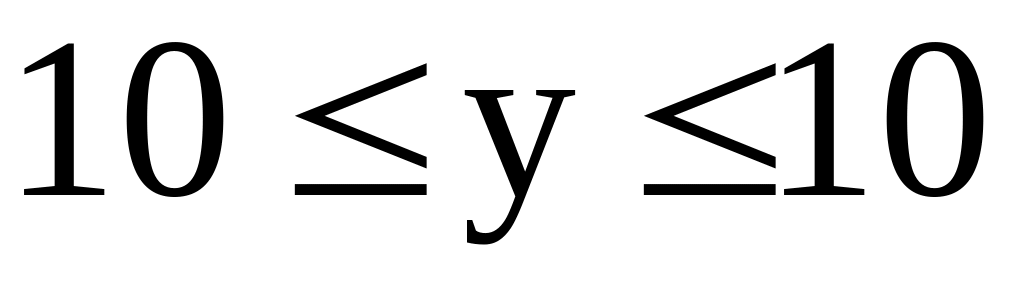(функція CONTOUR).

  5. Побудувати графік функції в області 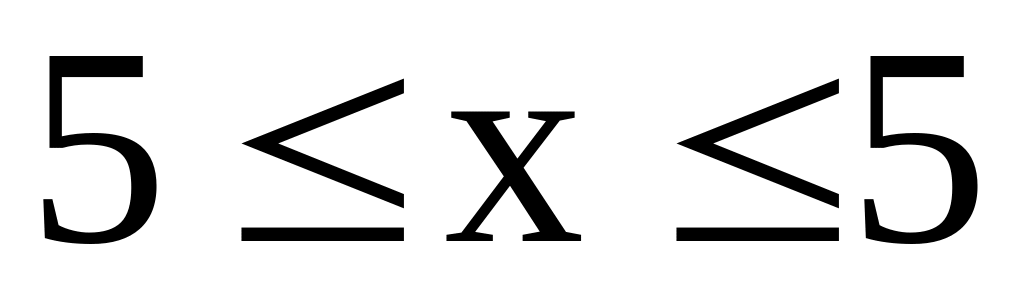, 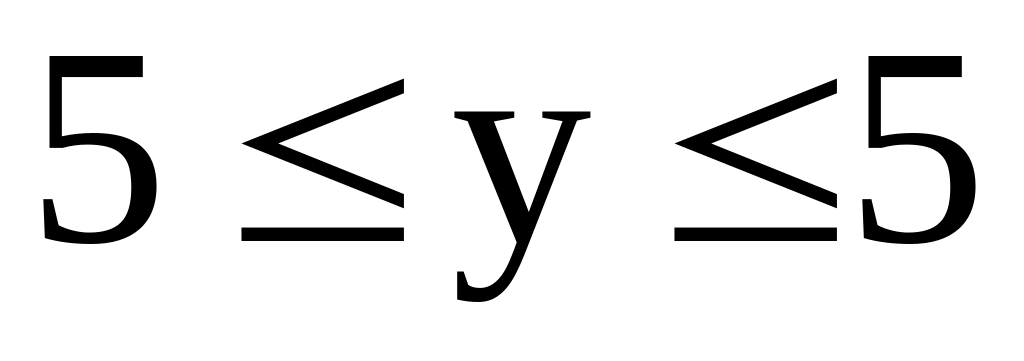(функції MESH та PLOT3).

  6.  Побудувати тривимірну затінену поверхню функції z = x*exp(-x2-y2) зі шкалою затемненості (функція SURF).

  7. Побудувати сферу, що розфарбована відповідно до матриці Адамара (Hadamard), часто використовуваної в теорії кодування сигналів і складеної тільки з двох чисел 1 і -1 (функція SURF).

  8. Побудувати тривимірну просторову спіраль (див. приклад).

  9. Побудувати сферу за колами (див. приклад).

Завдання 3: Розрахунок математичного виразу.

      1. Обчислити значення заданого виразу за допомогою середовища MatLab.

      2. Зібрати схему, еквівалентну даному виразу, використовуючи математичні блоки пакету розширення Simulink.

      3. Порівняти отримані значення.

Завдання 4.

1. Розв’язати нелінійну систему рівнянь, зібравши еквівалентну схему в Simulink.

2. Розв’язати нелінійну систему рівнянь засобами Matlab (процедура fsolve).

3. Порівняти отримані результати.

Варіанти до завдання 1:

Двовимірні графіки.

  1. Квадратриса.

  2. Логарифмічна спіраль.

  3. Нефроїда.

  4. Трактриса.

  5. Трохоїда.

  6. Ланцюгова лінія.

  7. Циклоїда.

  8. Циклоїдальна крива.

  9. Епіциклоїда.

  10. Овал Кассині.

  11. Архімедова спіраль.

  12. Гіперболічна спіраль

  13. Циклоїда.

  14. Астроїда.

  15. Архімедова спіраль.

  16. Гіперболічна спіраль

  17. Декартів лист.

  18. Епіциклоїда.

  19. Архімедова спіраль.

  20. Гіперболічна спіраль.

  21. Гіпоциклоїда.

  22. Квадратриса.

  23. Логарифмічна спіраль.

Тривимірні графіки.

  1. Дійсний конус: x = a u cos v, y = b u sin v, z = cu.

  2. Еліптичний циліндр: x = a cos v, y = b sin v, z = u.

  3. Еліпсоід: x = a sin u cos v, y = b sin u cos v, z = c sin u cos v.

  4. Однополосний гіперболоід: x = a ch u cos v, y = b ch u sin v, z = c sh u.

  5. Двуполосний гіперболоїд: x = ± a ch u, y = b sh u sin v, z = c sh u cos v.

  6. Еліптичний параболоїд: x = a u cos v, y = b u cos v, z=0.5u2.

  7. Гіперболічний параболоїд: x = a u ch v, y = b u ch v, z=0.5u2.

  8. Дійсний конус: x = a u cos v, y = b u sin v, z = cu.

  9. Однополосний гіперболоїд: x = a ch u cos v, y = b ch u sin v, z = c sh u.

  10. Двуполосний гіперболоїд: x = ± a ch u, y = b sh u sin v, z = c sh u cos v.

  11. Еліптичний параболоїд: x = a u cos v, y = b u cos v, z=0.5u2.

  12. Гіперболічний параболоїд: x = a u ch v, y = b u ch v, z=0.5u2.

  13. Дійсний конус: x = a u cos v, y = b u sin v, z = cu.

  14. Еліптичний циліндр: x = a cos v, y = b sin v, z = u.

  15. Еліпсоід: x = a sin u cos v, y = b sin u cos v, z = c sin u cos v.

  16. Однополосний гіперболоїд: x = a ch u cos v, y = b ch u sin v, z = c sh u.

  17. Двуполосний гіперболоїд: x = ± a ch u, y = b sh u sin v, z = c sh u cos v.

  18. Еліптичний параболоїд: x = a u cos v, y = b u cos v, z=0.5u2.

  19. Гіперболічний параболоїд: x = a u ch v, y = b u ch v, z=0.5u2.

  20. Дійсний конус: x = a u cos v, y = b u sin v, z = cu.

  21. Еліптичний циліндр: x = a cos v, y = b sin v, z = u.

  22. Еліпсоїд: x = a sin u cos v, y = b sin u cos v, z = c sin u cos v.

  23. Однополосний гіперболоїд: x = a ch u cos v, y = b ch u sin v, z = c sh u.

Варіанти до завдання 2:

Варіант

Завдання

Побудувати залежність cos(x), якщо x є послідовність чисел від 1 до 36.

  1. Для значень x, що змінюється у межах від –1 до 30 із кроком 0.1, побудувати графіки в одному вікні за функціями cos(3*x), sin(2*x+0.9), cos(x) та графіки поверхні рівнів і поверхні.

  1. Побудувати залежність tg(x), якщо x є послідовність чисел від 0 до 20.

  2. Для значень x, що змінюється у межах від –5 до 20 із кроком 0.2, побудувати графіки в одному вікні за функціями sin(4*x), cos(4*x+0.5), tg(5*x) та графіки поверхні рівнів і поверхні.

  1. Нехай деяка залежність y(x) задана векторами координат її точок X = ( 5, 7, 9, 11, 13), Y = (5.2, 6.3, 6.5, 7.4, 7.6). Вивести поліноміальну регресію для степенів полі­нома 2 та 3.

  2. Для значень x, що змінюється у межах від 0 до 20 із кроком 0.2, побудувати графіки в одному вікні за функціями ctg(3*x), tg(3*x+0.3), sin(x) та графіки поверхні рівнів і поверхні.

  1. Побудувати залежність sin(x), якщо x є послідовність чисел від 0 до 40.

  2. Для значень x, що змінюється у межах від –2 до 20 із кроком 0.1, побудувати графіки в одному вікні за функціями cos(3*x), sin(4*x+0.3), tg(x) та графіки поверхні рівнів і по­верхні.

  1. Дана деяка залежність y(x) векторами координат її точок: X= (2, 4, 6, 8, 10, 12, 14, 16), Y= (3.6, 4.5, 5.3, 5.7, 6.4, 6.7, 6.9, 7.2). Побудувати поліноміальну регресію залежності для степенів полінома 2, 3 та 6.

  2. Для значень x, що змінюються у межах від -4 до 12 із кроком 0.2, побудувати графіки за функціями sin(4*x), tg(3*x+0.7), cos(x) та графіки поверхні рівнів і поверхні.

  1. Дана деяка залежність y(x) векторами координат її точок: X= (2, 4, 6, 8, 10, 12, 14, 16,18), Y= (3.8, 4.9, 5.5, 5.9, 6.7, 6.8, 6.9, 7.5, 7.8). Побудувати поліноміальну регресію за­лежності для степенів полінома 3,4 та 6.

  2. Для значень x, що змінюються у межах від -2 до 18 із кроком 0.2, побудувати графіки за функціями sin(2*x), tg(2*x+0.6), cos(3*x) та графіки поверхні рівнів і поверхні.

  1. Дана деяка залежність y(x) векторами координат її точок: X=(6, 8, 10, 12), Y=(5.3, 5.7, 6.4, 6.7). Побудувати поліно­мі­альну регресію залежності для степенів полінома 2, 3 та 4.

  2. Для значень x, що змінюються у межах від -6 до 20 із кроком 0.1, побудувати графіки за функціями cos(3*x), tg(3*x+0.7), sin(4*x) та графіки поверхні рівнів і поверхні.

  1. Дана деяка залежність y(x) векторами координат її точок: X= (2, 4, 6, 8, 10, 12, 14), Y= (3.76, 4.4, 5.1, 5.56, 6, 6.3, 6.7). Побудувати поліноміальну регресію залежності для степенів полінома 1, 2, 3 та 6.

  2. Для значень x, що змінюються у межах від –2 до 10 із кроком 0.1, побудувати графіки в одному вікні за функціями cos(4*x), sin(3*x+0.7), cos(2*x) та графіки поверхні рівнів і поверхні.

  1. Побудувати залежність cos(x), якщо x є послідовність чисел від 1 до 30.

  2. Для значень x, що змінюється у межах від –3 до 10 із кроком 0.1, побудувати графіки за функціями cos(7*x), sin(3*x+0.8), cos(3*x) та графіки поверхні рівнів і поверхні.

  1. Дана деяка залежність y(x) векторами координат її точок: X= (2, 4, 6, 8, 10, 12, 14), Y= (3.76, 4.4, 5.1, 5.56, 6, 6.3, 6.7). Побудувати поліноміальну регресію залежності для степенів полінома 1, 2, 3 та 6.

  2. Для значень x, що змінюється у межах від –2 до 20 із кроком 0.2, побудувати графіки в одному вікні за функціями cos(3*x), sin(5*x+0.3), cos(x) та графіки поверхні рівнів і поверхні.

  1. Нехай деяка залежність y(x) задана векторами координат її точок X = (2, 4, 6, 8, 10), Y = (3.7, 4.4, 5.15, 5.6, 6.9). Вивести поліноміальну регресію для лінійної та параболічної регресії.

  2. Для значень x, що змінюється у межах від –2 до 10 із кроком 0.1, побудувати графіки за функціями cos(4*x), sin(3*x+0.7), cos(4*x) та графіки поверхні рівнів і поверхні.

  1. Нехай деяка залежність y(x) задана векторами координат її точок X = (2, 4, 6, 8, 10), Y = (3.7, 4.4, 5.15, 5.6, 6.9). Вивести поліноміальну регресію для лінійної, параболічної, кубічної регресії.

  2. Для значень x, що змінюється у межах від –3 до 10 із кроком 0.1, побудувати графіки в одному вікні за функціями cos(7*x), sin(3*x+0.8), cos(3*x) та графіки поверхні рівнів і поверхні.

  1. Побудувати залежність sin(x), якщо x є послідовність чисел від 1 до 40.

  2. Для значень x, що змінюється у межах від –2 до 10 із кроком 0.1, побудувати графіки в одному вікні за функціями cos(4*x), sin(3*x+0.7), cos(x) та графіки поверхні рівнів і поверхні.

  1. Нехай деяка залежність y(x) задана векторами координат її то­чок X = (2, 4, 6, 8, 10), Y = (3.7, 4.4, 5.15, 5.6, 6.9). На графіку ви­вести поліноміальну регресію для лінійної та кубічної регресії

  2. Для значень x, що змінюється у межах від –3 до 10 з кроком 0.1, побудувати графіки в одному вікні за функціями cos(7*x), sin(3*x+0.8), cos(3*x) та графіки поверхні рівнів і поверхні.

  1. Побудувати залежність tg(x), якщо x є послідовність чисел від 1 до 20.

  2. Для значень x, що змінюється у межах від –1 до 30 із кроком 0.1, побудувати графіки в одному вікні за функціями tg(3*x), cos(2*x+0.9), sin(x) та графіки поверхні рівнів і поверхні.

  1. Нехай деяка залежність y(x) задана векторами координат її точок X = ( 4, 6, 8, 10), Y = ( 4.5, 5.2, 5.7, 6.9). На графіку вивести поліноміальну регресію для лінійної, параболічної, кубічної регресії

  2. Для значень x, що змінюється у межах від 0 до 10 з кроком 0.1, побудувати графіки в одному вікні за функціями tg(7*x), sin(6*x+0.5), cos(2*x) та графіки поверхні рівнів і поверхні.

  1. Дана деяка залежність y(x) векторами координат її точок: X= (2, 4, 6, 8, 10, 12), Y= (3.6, 4.7, 5.6, 5.8, 6, 6.5). Побудувати полі­номіальну регресію залежності для степенів полінома 2, 3,4.

  2. Для значень x, що змінюються у межах від –2 до 16 із кроком 0.2, побудувати графіки в одному вікні за функціями sin(4*x), tg(3*x+0.8), cos(x) та графіки поверхні рівнів і поверхні.

  1. Дана деяка залежність y(x) векторами координат її точок: X= (1, 2, 3, 4, 5, 6, 7, 8), Y= (2.6, 3.7, 4.6, 4.8, 5.1, 5.5, 6, 6.3). По­бу­дувати поліноміальну регресію залежності для степенів полінома 4, 5,6.

  2. Для значень x, що змінюються у межах від 0 до 26 із кроком 0.1, побудувати графіки в одному вікні за функціями sin(2*x), cos(3*x+0.4), sin(x) та графіки поверхні рівнів і поверхні.

  1. Побудувати залежність cos(x), якщо x є послідовність чисел від 1 до 36.

  2. Для значень x, що змінюється у межах від –1 до 30 із кроком 0.1, побудувати графіки в одному вікні за функціями cos(3*x), sin(2*x+0.9), cos(x) та графіки поверхні рівнів і поверхні.

  1. Побудувати залежність tg(x), якщо x є послідовність чисел від 0 до 20.

  2. Для значень x, що змінюється у межах від –5 до 20 із кроком 0.2, побудувати графіки в одному вікні за функціями sin(4*x), cos(4*x+0.5), tg(5*x) та графіки поверхні рівнів і поверхні.

  1. Нехай деяка залежність y(x) задана векторами координат її точок X = ( 3, 5, 7, 9, 11, 13), Y = ( 4.4, 5.2, 6.3, 6.5, 7.4, 7.6). Вивести поліноміальну регресію для степенів полінома 1, 2 та 3.

  2. Для значень x, що змінюється у межах від –2 до 20 із кроком 0.1, побудувати графіки в одному вікні за функціями tg(3*x), sin(2*x+0.4), sin(x) та графіки поверхні рівнів і поверхні.

Варіанти до завдання 3:

Варіант

Вираз

Варіанти до завдання 4:

№ вар.

Нелінійна система рівнянь

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности