Раздел 2. Элементы математического анализа.

№ 6. Тема 2.1. Множества и операции над множествами. (2 часа - лекция).

План:

1. Понятие множества.

2. Элементы множества.

3. Подмножества.

4. Пересечение множеств.

5. Объединение множеств.

6. Вычитание множеств.

7. Дополнение до множества.

8. Числовые множества.

Понятие множества – одно из первичных в математике. Множество представляет собой соединение, совокупность, собрание некоторых предметов, объединенных по какому – либо признаку. Например: множество букв алфавита, множество чисел первого десятка, множество точек на прямой, множество книг на полке и т.д.

Элементы множества – это то, из чего это множество состоит, например: буква «к» - это элемент множества букв русского алфавита.

Множества обычно обозначают заглавными буквами латинского алфавита А, В, С, N,… или запись со скобками 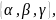а элементы этих множеств – аналогичными маленькими буквами: 𝒂, b, c, n …

Существуют стандартные обозначения для некоторых множеств. Например,

Z - множество целых чисел;

Q - множество рациональных чисел;

I - множество иррациональных чисел;

R - множество действительных чисел;

C - множество комплексных чисел.

Если элемент 𝒂 принадлежит множеству А, пишут 𝒂

Запись 𝒂 означает, что элемент 𝒂 не принадлежит множеству А.

Множество считается заданным, если или перечислены все его элементы, или указано такое свойство его элементов, которое позволяет судить о том, принадлежит данный элемент множеству или нет.

Множество, содержащее конечное число элементов, называется конечным.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается . Пишут: А = .

Множества, состоящие из одних и тех же элементов, называются равными. Пишут: А = В.

Если любой элемент множества А является элементом другого множества В, то говорят, что А есть подмножество множества В. Пишут: А (А содержится в В).

Например: 1) Множество всех натуральных чисел N является подмножеством всех действительных чисел R, т.е. N⊂ R. Из определения ⟹ любое множество является своим подмножеством.

2)Рассмотрим множество учеников некоторого класса; обозначим это множество Х, и пусть Y – множество учеников того же класса, получивших за контрольную по истории оценку « отлично». Если все ученики класса получили за эту контрольную оценку « отлично», то X и Y равные множества: X = Y; Если же ни один ученик класса не получил « отлично», то множество Y – пустое: Y = .Но в любом случае множество Y является подмножеством множества X: Y .

Пример: Найти все подмножества множества А = .

Ответ: .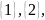

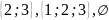Число всех подмножеств равно восьми. Т.о. любое множество, состоящее из трех элементов, имеет 8 = подмножеств. Если множество состоит из n элементов, то число всех его подмножеств равно .

В математике часто приходится иметь дело с числовыми множествами. Приведём определения и обозначения множеств, которые имеют общее название числовых промежутков.

Название промежутка Определение Обозначение Отрезок от a до b (замкнутое множество) a ≤ x ≤ b [a; b] Интервал от a до b (открытое множество) a < x < b (a; b) Открытый слева промежуток от a до b a < x ≤ b (a; b] Открытый справа промежуток от a до b a ≤ x < b [a; b) Закрытый числовой луч от a до +∞ x ≥ a [a; +∞) Открытый числовой луч от a до +∞ x > a (a; +∞) Закрытый числовой луч от −∞ до a x ≤ a (−∞; a] Открытый числовой луч от −∞ до a x < a (−∞; a) Числовая прямая −∞ < x < +∞

Пример 1

Задайте перечислением множество B = {x: x² − 2x + 1 = 0}. Это стандартная запись для задания множества, читается она так: множество элементов x таких, что x² − 2x + 1 = 0.

Решение

Так как уравнение x2 − 2x + 1 = 0 имеет единственный корень x = 1, то множество B состоит из одного элемента B = {1}. Ответ. B = {1}.

Пример 2. Определите множество A натуральных чисел, меньших   .

Решение

Так как любое натуральное число больше 1 и тем более    ,то натуральных чисел, обладающих указанным свойством, не существует, и A =  . Ответ. A =

Мощностью конечного множества называется количество его элементов. Мощность множества A  обозначается m (A).

Пример 1

Определите мощность множества A = {1, 3, 5, 7, 9} нечётных чисел.

Решение

Простым пересчётом элементов убеждаемся, что нечётных чисел всего 5, и потому m (A) = 5. Ответ. 5.

Ясно, что понятие мощности конечных множеств позволяет сравнивать их по количеству элементов. Так, если A = {1, 3, 5, 7, 9}, а B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4 и потому m (A) > m (B).

Однако если мы имеем дело с бесконечными множествами, то пересчитать элементы множества уже не удастся. Но иногда можно установить взаимно однозначное соответствие между двумя бесконечными множествами.

Говорят, что между множествами A и B установлено взаимно однозначное соответствие, если из элементов этих множеств можно составить пары (a, b), причем каждый элемент из A и каждый элемент из B входят в одну и только одну пару.

Множества A и B называют равномощными, если между их элементами можно установить взаимно однозначное соответствие .

Множества, равномощные множеству натуральных чисел, называются счётными множествами.

Пример 2

Множество натуральных чисел равномощно множеству нечётных чисел, так как между ними можно установить взаимно однозначное соответствие, например, по следующему правилу:

1	2	3	...	n	...
↕	↕	↕		↕
1	3	5	...	2n – 1	...

Так как множество нечётных чисел является подмножеством натуральных чисел, то этот пример показывает, что бесконечное множество может быть равномощно своему подмножеству.

Пример 3

Множество положительных рациональных чисел счётно. Действительно, если представить каждое рациональное число в виде несократимой дроби и записать его в следующую таблицу, а затем пронумеровать, как указано на рисунке, то окажется, что множество рациональных положительных чисел действительно счётно.

Рисунок 2 Счётность множества рациональных чисел

Операции над множествами:

Рассмотрим некоторое множество Е, которое будем называть основным, и не будем интересоваться его природой. Будем считать, что все множества, которые рассматриваются в данном пункте, являются подмножествами основного множества.