20. Задача лп с параметром в функции цели и правых частях ограничений, свойства решающей функции и области разрешимости.

F(x,λ)=(c1’+ λc1”)x1+(c2’+ λc2”)x2+…+(cj’+ λcj”)xj+…+(cn’+ λcn”)xnmax

cj’+ λcj” – цены

λ – скалярный параметр (показывает темп изменения цен реализации)

λ ≤ λ ≤ λ (м.б. время)

Возможные результаты:

считается, что задача разрешима при λ = 0

0 ≤ λ ≤ λ (исследуется вправо до заданной величины)

С ростом параметра λ значение может меняться

х 2

Р

Q

R

х1

Существует область устойчивости при изменении параметра λ – область в которой сохраняются признаки текущей вершины

Теорема. Область представляет собой связанное множество относительно параметра. Область является связанной и состоит из конечного числа локальных областей устойчивости. Область не разрешима, если она представляет собой луч с выколотым началом.

Каждая локальная область м.б. точкой или отрезком или лучом.

Теорема: Решающая функция является кусочно-линейной в области разрешимости. Ее коэффициенты возрастают нестрого монотонно при переходе из точки излома слева направо. В каждой области устойчивости ф-ция линейна.

Теорема: Алгоритм симплекс-типа со специальными правилами перехода от текущего базиса к следующему позволяет полностью исследовать модель за конечное число шагов при условии, что предпринимаются меры против зацикливания процессов.

PQR

F(λ) ~ F(λ) ~ F(λ)

Если цепочка состоит из более, чем 5 вершин, то возникает цикл.

Практическое применение модели: 1) цены; 2) выпуск железа; 3) глубина обогащения сырья.

С помощью обычных программ такая модель может быть исследована путем последовательного изменения коэффицентов функции целей.

Области устойчивости при этом не определяются, график функции при этом F(λ) будет получен.

При изменении параметра λ, меняется оценка оптимальности Δj

Δj = Δj’+ λΔj” ≥ 0 j=1,n

Оценки ресурсов: yi* , i=1,m y* = yi*

В каждой области устойчивости свой фикс. вектор оценок на ресурсы.

Типы моделей, для которых используются строгие эффективные методы:

1) Функция цели зависит от λ – PARAOBJ, F(x, λ)

2) Функция цели зависит от параметра b’+μb” – PARARHS

3) зависимость от t

4) два различных параметра – λ и μ

5) Любая строка матрицы условий зависит от параметра PARAROW (параметры вводятся только в строки)

(ai1*+µai1**) -1й элемент

(аi2*+µаi2**) – 2й элемент

0≤µ≤µ - количественный параметр

аi2* - коэф-т расхода сырья

аi2** - темпы изменения по линейному закону

6) Любой столбец зависит от параметра PARACOL (столбцы условий) Когда вводятся параметры в столбцы. Третий случай – когда добавляются ещё цены реализации 0≤t≤t’

Функция второго порядка F(t)=F*+tF**+t²F***

Цены меняются вне зависимости от запасов на складе – двухпараметрическая модель

8. Направления параметризации задачи лп для учета неопределенности будущих условий экономической операции. Типы получаемых проблем.

Рассматривается задача ЛП, в которой требуется найти максимум линейной формы L=(C,X)MAX при условиях AX≤B и X≥0, причем элементы вектора ограничений, элементы матрицы условий и коэффициенты функции цели могут быть случайными числами как с известными характеристиками (случай риска), так и неизвестными (случай неопределенности).

Если задача полностью стохастическая, то необходимо уточнить исходную постановку задачи: определить, что понимается под допустимым решением (планом), а также смысловое содержание показателя качества решений. Исходной задаче может соответствовать различные определения (модели) стохастической задачи: 

1) Решение задачи Х рассматривается как детерминированный (фиксированный) вектор; допустимым решением (планом) считается такой вектор Х, который удовлетворяет ограничениям задачи при всех возможных сочетаниях значений А и В, имеющих положительную вероятность; это жесткая постановка задачи, не использующая дополнительных сведений относительно статистических характеристик условий в модели.

A(q)*X<=B(q) для всех q@Q,X>=0 

Здесь q‑случайные параметры, от которых зависят значения А и В (состояния природы), их набор обычно считается конечным;

2) Во многих ситуациях нецелесообразно исключать из рассмотрения ситуации, которым соответствуют относительно небольшие невязки в условиях задачи либо эти невязки возможны при некоторых сочетаниях случайных параметров, характеризующихся низкой вероятностью; рациональнее учесть некоторые потери («штраф») в показателе качества решения, зависящий от величины невязки (затраты на адаптирующие мероприятия); такая постановка называется нежесткой; соответствующая модель называется двухэтапной - ее исследование проводится в два этапа: на первом определяется некоторый вектор Х не обязательно удовлетворяющий всем ограничениям задачи; на втором - в зависимости от невязки АХ‑В вводится вектор R, корректирующий решение; обычно такие задачи имеют в качестве критерия минимум математического ожидания суммы значений функции цели и штрафа за невязки.

8. Схема преобразования стохастической задачи МП к эквивалентному детерминированному виду. Содержательное истолкование детерминированной задачи.

Рассматривается задача ЛП, в которой требуется найти максимум линейной формы L=(C,X)MAX при условиях AX≤B и X≥0, причем элементы вектора ограничений, элементы матрицы условий и коэффициенты функции цели могут быть случайными числами как с известными характеристиками (случай риска), так и неизвестными (случай неопред-ности).

Если задача полностью стохастическая, то необходимо уточнить исходную постановку задачи: определить, что понимается под допустимым решением (планом), а также смысловое содержание показателя качества решений. Исходной задаче может соответствовать различные определения (модели) стохастической задачи: 

Если случайны не только вектор С, но и другая информация: вектор В и матрица условий А, то необходимо уточнить исходную постановку задачи: определить, что понимается под допустимым решением (планом), а также смысловое содержание показателя качества решений.

Решение задачи Х рассматривается как детерминированный (фиксированный) вектор; допустимым решением (планом) считается такой вектор Х, который удовлетворяет ограничениям задачи при всех возможных сочетаниях значений А и В, имеющих положительную вероятность; это жесткая постановка задачи, не использующая дополнительных сведений относительно статистических характеристик условий в модели.

A(q)*X<=B(q) для всех q@Q,X>=0 Здесь q‑случайные параметры, от которых зависят значения А и В (состояния природы), их набор обычно считается конечным;

Р(SUM Aij*Xj <= Bi) >= Pi; i=1,...,m; 0 =< Pi <= 1 при этом часто матрица А предполагается фиксированной и случаен только вектор ограничений В; если множество возможных состояний природы конечно и известны характеристики (оценки значений и их вероятностей) для каждого элемента Вi (т.е. Bki и Hki для k=1,...,s), то можно определить значения ~Bi, которые удовлетворяют условию P(Bi(q)>=~Bi)>=Pi; действительно, для этого необходимо упорядочить значения Bki в порядке убывания и выбрать наименьшую группу, удовлетворяющую условию: вероятность попадания значения Bi в данную группу больше или равна Pi (для этого суммарная вероятность группы должна быть больше или равна Pi). Тогда задача будет сведена к детерминированной: (^C,X)MAX AX<=~B, где ~B=(~B1,~B2,...,~Bm) при условии жесткой постановки (одноэтапной);

Нахождение решения стохастической задачи в жесткой постановке может быть организовано следующим образом:

- если X - допустимый план (перманентное решение) задачи, то он удовлетворяет соотношению A^X<=B^ для любой допустимой (возможной) пары [A^,B^].

Обычный подход сводится к рассмотрению решения детерминированной задачи, полученной заменой вероятностных условий их математическими ожиданиями; после этого проверяется перманентность плана (в случае ограниченности элементов матрицы А и В это несложно)

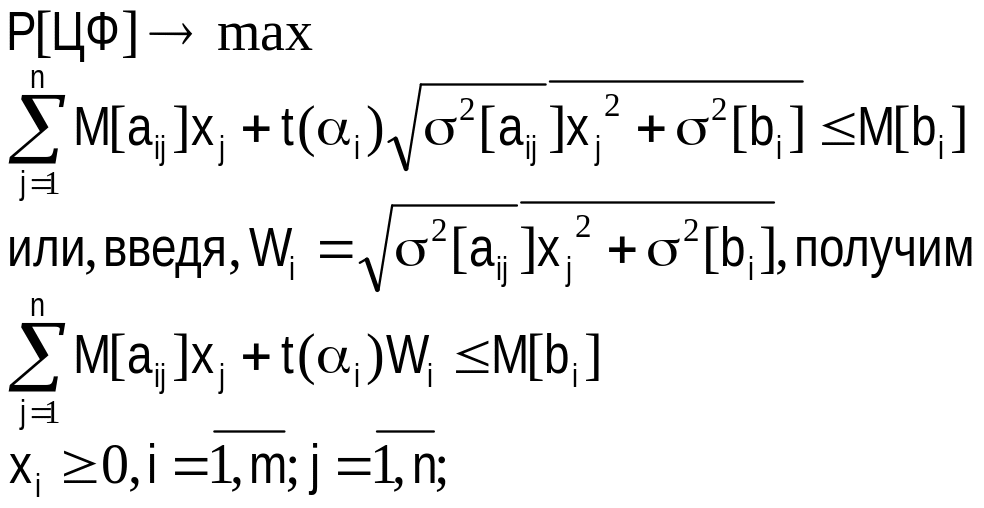
8. Формулировка двух типов задач поиска решений при использовании детерминированного эквивалента стохастической задачи МП на максимум математического ожидания функции цели и на максимум вероятности (надежности) достижения заданного уровня функции цели.

Рассматривается задача ЛП, в которой требуется найти максимум линейной формы L=(C,X)MAX при условиях AX≤B и X≥0, причем элементы вектора ограничений, элементы матрицы условий и коэффициенты функции цели могут быть случайными числами как с известными характеристиками (случай риска), так и неизвестными (случай неопределенности).

1) все значения заменяются на мат. ожидании (среднее значение) – максимизация результата при заданной надежности P ≥ Р при F max

Случаен только вектор С функции цели, остальная информация детерминирована. Обычный в этой ситуации подход - выбор в качестве критерия математического ожидания функции цели - сводит задачу к детерминированной (критерий имеет вид (^C,X)MAX, где ~С - математическое ожидание вектора С). Если статистические характеристики вектора С неизвестны, то применяются различные гипотезы и оценки, а также методы анализа зоны неопределенности.

2) максимизация надежности при заданном уровне эффекта F ≥ F при maxP(F). Если случайны не только вектор С, но и другая информация: вектор В и матрица условий А, то необходимо уточнить исходную постановку задачи: определить, что понимается под допустимым решением (планом), а также смысловое содержание показателя качества решений.

Р(SUM Aij*Xj <= Bi) >= Pi; i=1,...,m; 0 =< Pi <= 1 при этом часто матрица А предполагается фиксированной и случаен только вектор ограничений В; если множество возможных состояний природы конечно и известны характеристики (оценки значений и их вероятностей) для каждого элемента Вi (т.е. Bki и Hki для k=1,...,s), то можно определить значения ~Bi, которые удовлетворяют условию P(Bi(q)>=~Bi)>=Pi; действительно, для этого необходимо упорядочить значения Bki в порядке убывания и выбрать наименьшую группу, удовлетворяющую условию: вероятность попадания значения Bi в данную группу больше или равна Pi (для этого суммарная вероятность группы должна быть больше или равна Pi). Тогда задача будет сведена к детерминированной: (^C,X)MAX AX<=~B, где ~B=(~B1,~B2,...,~Bm)