15. Лабораторна робота №16

17. Використання процедур і функцій мп Turbo Pascal при опрацюванні масивів даних.

17. Навчитися використовувати процедури при опрацюванні масивів даних.

Задача №1

Постановка задачі

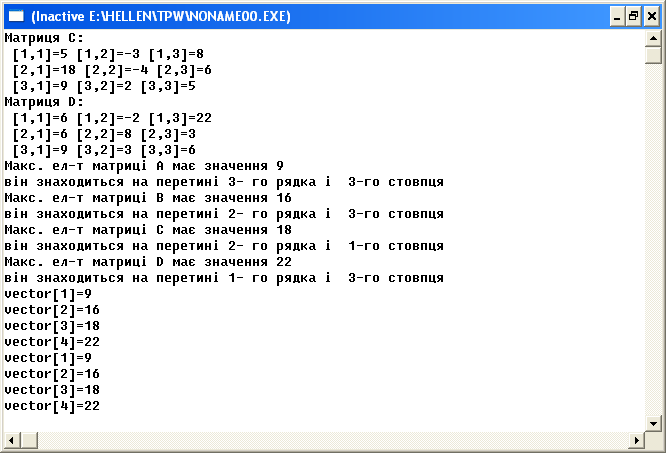
Задані чотири матриці A[n:m], B[n:m], C[n:m], D[n:m] (n=3, m=3). Знайти максимальний елемент кожної матриці і створити з цих елементів вектор. Упорядкувати елементи вектора за зростанням.

program max_matrix;

uses wincrt;

const n=3; m=3;

type MyMatrix=array[1..n,1..m] of integer;

var A,C,B,D:MyMatrix;

i,j,k,buf:integer;ni,nj,maxA,maxB,maxC,maxD:integer;

vector:array[1..4] of integer;

procedure form_Matr(n1,m1:integer; var Matrix:MyMatrix);

begin

for i:=1 to n1 do

begin

for j:=1 to m1 do

begin

write('введіть [',i,',',j,']=>');

read(Matrix[i,j]);

end;

readln;

end;

end;

procedure Matr_na_ekran(n1,m1:integer; var Matrix:MyMatrix);

begin

for i:=1 to n1 do

begin

for j:=1 to m1 do

write(' [',i,',',j,']=',Matrix[i,j]);

writeln;

end;

end;

procedure max_M(n1,m1:integer; var Matrix:MyMatrix; var_ imaxM,jmaxM,maxM:integer; nameM:string);

begin

maxM:=Matrix[1,1];

imaxM:=1;

jmaxM:=1;

for i:=1 to n1 do

for j:=1 to m1 do

if Matrix[i,j]>maxM

then

begin

maxM:=Matrix[i,j];

imaxM:=i;

jmaxM:=j

end;

writeln('Макс. елемент матриці',nameM,' має значення ',maxM);

writeln('він знаходиться на перетині',imaxM,'- го рядка ³ ',jmaxM, '-го стовпця');

end;

begin

{формування матриць}

writeln('введіть елементи матриці À:');

form_Matr(n,m,A);

writeln(' введіть елементи матриці B:');

form_Matr(n,m,B);

writeln(' введіть елементи матриці C:');

form_Matr(n,m,C);

writeln(' введіть елементи матриці D:');

form_Matr(n,m,D);

writeln('матриця À:');

{виведення матриць на екран}

Matr_na_ekran(n,m,A);

writeln('матриця B:');

Matr_na_ekran(n,m,B);

writeln('матриця C:');

Matr_na_ekran(n,m,C);

writeln('матриця D:');

Matr_na_ekran(n,m,D);

{пошук максимального елемента матриць}

Max_M(n,m,A,ni,nj,maxA,'A');

Max_M(n,m,B,ni,nj,maxB,'B');

Max_M(n,m,C,ni,nj,maxC,'C');

Max_M(n,m,D,ni,nj,maxD,'D');

{формування вектора з макс. елементів матриць}

vector[1]:=maxA; vector[2]:=maxB; vector[3]:=maxC; vector[4]:=maxD;

{впорядкування вектора}

for i:=1 to 4 do

writeln('vector[',i,']=',vector[i]);

for k:=4 downto 2 do

for i:=1 to k-1 do

if vector[i]>vector[i+1]

then

begin

buf:=vector[i];

vector[i]:=vector[i+1];

vector[i+1]:=buf;

end;

for i:=1 to 4 do

writeln('vector[',i,']=',vector[i])

end.

Задача №2

Постановка задачі

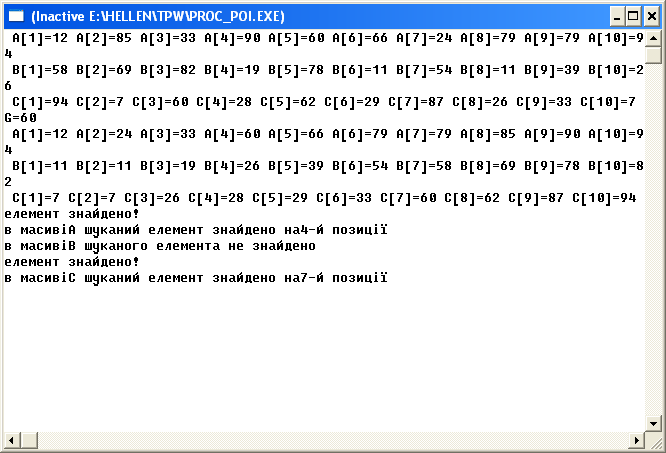
Задані три вектори A[n], B[n], C[n], n=10. Задано число G=13. Дати відповідь на питання: „Чи є серед елементів векторів A,B,C елемент, який має значення числа G?”

program proc_poisk;

uses wincrt;

const n=10;

type MyVect=array[1..n] of integer;

var A,B,C:MyVect;

i:integer;

G:integer;

procedure form_vect(n1:integer; var Vector:MyVect; Name:string);

begin

for i:=1 to n1 do

vector[i]:=random(100);

for i:=1 to n1 do

write(' ',Name,'[',i,']=',vector[i]);

writeln

end;

procedure bulb(n1:integer;var Vector:MyVect; Name:string);

var k:integer; buf:integer;

begin

for k:=n1 downto 2 do

for i:=1 to k-1 do

if vector[i]>vector[i+1]

then

begin

buf:=vector[i];

vector[i]:=vector[i+1];

vector[i+1]:=buf;

end;

for i:=1 to n1 do

write(' ',name,'[',i,']=',vector[i]);

writeln;

end;

procedure poisk(n1:integer;var Vector:MyVect; name:string);

var l,r:integer;

begin

l:=1;

r:=n;

while (l<=r) do

begin

i:=(l+r) div 2;

if vector[i]=G

then begin

l:=10000;

writeln('елемент знайдено!')

end

else if vector[i]<G

then l:=i+1

else r:=i-1;

end;

if vector[i]=G

then writeln('в масиві',Name,' шуканий елемент знайдено на',i,'-й позиції')

else writeln('в масиві',Name,' шуканого елемента не знайдено');

end;

begin

randomize;

form_Vect(n,A,'A');

form_Vect(n,B,'B');

form_Vect(n,C,'C');

writeln('G=');

readln(G);

bulb(n,A,'A');

bulb(n,B,'B');

bulb(n,C,'C');

poisk(n,A,'A');

poisk(n,B,'B');

poisk(n,C,'C');

end.

№16

Скласти блок-схему алгоритму розв’язання задачі відповідно до варіанту, зобразити її засобами Microsoft Word, написати програму мовою Pascal, відлагодити її та проаналізувати отримані результати [1].

№1

Задано три вектори Впорядкувати вектор за зростанням, який складається із компонентів:

b₁ – максимальне по модулю значення компонент вектора Х;

b₂ – максимальне по модулю значення компонент вектора Y;

b₃ – максимальне по модулю значення компонент вектора Z.

Пошук максимального по модулю значення компонент вектора оформити у вигляді підпрограми.

№2

Задано три вектори . Знайти розв’язок рівняння

сx=b , де

с – сума компонент вектора Х1=X Y;

d – сума компонент вектора Y1=Z Y

Обчислення добутку векторів і знаходження суми компонент вектора оформити у вигляді підпрограми.

№ 3

Задано два вектори . Обчислити

с – середнє арифметичне від’ємних компонент вектора X ;

d – середнє арифметичне від’ємних компонент вектора Y.

Обчислення середнього арифметичного від’ємних компонент вектора оформити у вигляді підпрограми.

№4

Задано три вектори Обчислити

p = acos + btg(a+b) ,

де =0,45;

а – скалярний добуток вектора X на вектор Z.

b – скалярний добуток вектора X на вектор Y.

Обчислення скалярного добутку оформити у вигляді підпрограми.

№5

Задано два вектори Обчислити

k – кількість додатних компонент вектора Х;

p – кількість додатних компонент вектора Y.

Обчислення кількості додатних компонент вектора оформити у вигляді підпрограми.

№6

Задано два вектори Обчислити

a – мінімальне значення компонент вектора Х;

k₁ – номер мінімального значення компонент вектора Х;

b – мінімальне значення компонент вектора Y;

k₂ – номер мінімального значення компонент вектора Y.

Пошук мінімального значення компонент вектора та його номера оформити у вигляді підпрограми.

№7

Задано три вектори Впорядкувати вектор за зростанням, який складається із компонентів:

с₁ – мінімальне значення компонент вектора Х;

с₂ – мінімальне значення компонент вектора Y;

с₃ – мінімальне значення компонент вектора Z.

Пошук мінімального значення компонент вектора оформити у вигляді підпрограми.

№ 8

Задано два вектори Обчислити

a – максимальне по модулю значення компонент вектора Х;

k – номер максимального по модулю значення компонент вектора Х;

b – максимальне по модулю значення компонент вектора Y;

L – номер максимального по модулю значення компонент вектора Y.

Пошук максимального по модулю значення компонент та його номера оформити у вигляді підпрограми.

№9

Задано чотири вектори З мінній а присвоїти значення 1, якщо скалярний добуток векторів X та Y більший скалярного добутку Z та P, в протилежному випадку присвоїти значення 0.

Обчислення скалярного добутку векторів оформити у вигляді підпрограми.

№ 10

Задано два вектори Обчислити

p – скалярний добуток вектора Х на вектор Х1, який складається із впорядкованих за зростанням компонент вектора Х;

r – скалярний добуток вектора Y на вектор Y1, який складається із впорядкованих за зростанням компонент вектора Y.

Обчислення скалярного добутку та впорядкування компонент вектора векторів оформити у вигляді підпрограми.

№ 11

Задано два вектори Розв’язати рівняння

ax=b , де

а – середнє геометричне додатних компонент вектора X ;

b – середнє геометричне додатних компонент вектора Y.

Обчислення середнього геометричного додатних компонент вектора оформити у вигляді підпрограми.

№12

З адано два вектори Обчислити

a – сума додатних компонент вектора Z;

b – сума додатних компонент вектора Y;

k₁ – кількість додатних компонент вектора Z;

k₂ – кількість додатних компонент вектора Y.

Обчислення суми та кількості додатних компонент вектора оформити в вигляді підпрограми.

№ 13

Задано два вектори . Обчислити

c – довжина вектора X1, який складається із від’ємних компонент вектора X;

d – довжина вектора Y1, який складається із від’ємних компонент вектора Y;

k₁ – кількість від’ємних компонент вектора X;

k₂ – кількість від’ємних компонент вектора Y.

Обчислення довжини вектора та формування векторів із від’ємних компонент вектора оформити у вигляді підпрограми.

№ 14

Задано два вектори Обчислити

с – мінімальне по модулю значення компонент вектора Х ;

d – мінімальне по модулю значення компонент вектора Y.

Пошук мінімального по модулю значення компонент вектора оформити у вигляді підпрограми.

№15

Задано три вектори Впорядкувати компоненти вектора за спаданням, який складається із компонент:

b₁ – сума парних компонент вектора Х;

b₂ – сума парних компонент вектора Y;

b₃ – сума парних компонент вектора Z.

Обчислення суми парних компонент вектора оформити у вигляді підпрограми

№16

Задано два вектора Змінній s присвоїти значення –1, якщо максимальне значення компонент вектора А більше за максимальне значення компонент вектора В, в протилежному випадку присвоїти значення 1 і присвоїти значення 0 , якщо максимальні значення компонент рівні.

Пошук максимального значення компонент вектора оформити у вигляді підпрограми.

№17

Задано три вектори Впорядкувати компоненти вектора за спаданням, який складається із компонент:

b₁ – максимальне значення компонент вектора Х;

b₂ – максимальне значення компонент вектора Y;

b₃ – максимальне значення компонент вектора Z.

Пошук максимального значення компонент вектора оформити у вигляді підпрограми.

№18

Задано три вектори Змінній w присвоїти значення 1, якщо довжина вектора d більша за довжину вектора с і значення 0 в протилежному випадку .

d – вектор, рівний сумі двох векторів X та Y ;

c – вектор, рівний сумі двох векторів Y та Z .

Обчислення суми двох векторів і знаходження довжини вектора оформити у вигляді підпрограми.

№19

З адано два вектора Обчислити

с – середнє геометричне модулів компонент вектора Z;

d – середнє геометричне модулів компонент вектора Y.

Обчислення середнього геометричного модулів компонент вектора оформити у вигляді підпрограми.

№20

Задано три вектори Впорядкувати за спаданням компоненти трьох векторів та знайти їх середнє арифметичне.

Впорядкування компонент вектора та обчислення його середнього арифметичного оформити у вигляді підпрограми.

№ 21

Задано два вектора Обчислити

a – кількість компонент вектора Z, більших за його середнє арифметичне;

b – кількість компонент вектора Y, більших за його середнє арифметичне.

Обчислення середнього арифметичного та кількості компонент вектора оформити у вигляді підпрограми.

№ 22

Задано два вектори . Обчислити

c – максимальне значення компонент вектора Z, компонентами якого є компоненти вектора X, що задовольняють умові –4  x_i  7;

d – максимальне значення компонент вектора Q, компонентами якого є компоненти вектора Y, що задовольняють умові –4  y_i  7;

k – номер максимального значення компонент вектора Z;

k₁ – номер максимального значення компонент вектора Q.

Пошук максимального значення компонент та його номера, а також формування компонент вектора за умовою оформити у вигляді підпрограми.

№ 23

Задано три вектори Обчислити

с – середнє геометричне додатних компонент вектора Z;

b – середнє геометричне додатних компонент вектора X;

d – середнє геометричне модулів компонент вектора Y.

Обчислення середнього геометричного додатних компонент вектора оформити у вигляді підпрограми.

№24

З адано три вектори Обчислити

a – сума скалярного добутку вектора Y на вектор Z і скалярного добутку вектора X на вектор Y;

b – різниця скалярного добутку вектора Y на вектор Z і скалярного добутку вектора X на вектор Y.

Обчислення скалярного добутку векторів оформити у вигляді підпрограми.

№25

З адано два вектори . Обчислити

c – максимальне значення компонент вектора X1, що складається із компонент вектора X, які задовольняють умові | xi | > 3;

d – максимальне значення компонент вектора Y1, що складається із компонент вектора Y, які задовольняють умові | yi | > 3;

Формування векторів та пошук максимального значення компонент вектора оформити у вигляді підпрограми.

№ 26

Задано два вектори Обчислити

с – середнє арифметичне модулів компонент вектора X, що задовольняють умові | x_i | >2;

с₁ – середнє арифметичне модулів компонент вектора Y, що задовольняють умові | y_i | >1;

d – максимальне значення компонент вектора X;

d₁ – максимальне значення компонент вектора Y.

Обчислення середнього геометричного додатних компонент та пошук максимального значення компонент вектора оформити у вигляді підпрограми.

№ 27

Задано два вектори Обчислити

a – скалярний добуток вектора X на вектор X1, компонентами якого є впорядковані за зростанням компоненти вектора X;

b – скалярний добуток вектора Z на вектор Z1, компонентами якого є впорядковані за зростанням компоненти вектора Z.

Обчислення скалярного добутку та впорядкування компонент векторів оформити у вигляді підпрограми.

№28

Задано три вектори Обчислити

с – довжина вектора X1, де X1= X +Y ;

s – довжина вектора Y1, де Y1= Y +Z .

Формування вектора, який дорівнює сумі двох векторів, та обчислення довжини вектора оформити у вигляді підпрограми.

№29

Задано три вектори Впорядкувати вектор за спаданням модулів компонент, який складається із компонент:

d₁ – добуток модулів компонент вектора X, розташованих на парних місцях;

d₂ – добуток модулів компонент вектора Y, розташованих на парних місцях;

d₃ – добуток модулів компонент вектора Z, розташованих на парних місцях.

Обчислення добутку модулів компонент вектора оформити у вигляді підпрограми.

№30

Задано два вектори Сформувати вектор Z, який складається спочатку із компонент вектора X1, а потім із компонент вектора Y1.

X1 – вектор, який складається із непарних компонент вектора X;

Y1 – вектор, який складається із непарних компонент вектора Y.

Формування вектора із непарних компонент оформити у вигляді підпрограми.

Модульний контроль №2

Контрольна робота №2