
- •Мфюа. Маси. Соболева в.В. Линейная алгебра. Лекция 1.
- •Тема 1. Векторная алгебра.
- •Системы координат на плоскости и в пространстве
- •2. Векторная алгебра
- •2.1. Понятие вектора. Линейные операции над векторами
- •2.2. Проекция вектора на ось. Свойства проекций.
- •С войства проекций
- •2.3. Координаты вектора. Координатная запись вектора.
- •2.4. Скалярное произведение векторов и его свойства.
- •Вычисление угла между векторами Из определения скалярного произведения и формул (2.5), (2.9) следует, что
- •Вычисление проекции одного вектора на другой
- •Условие перпендикулярности векторов
- •2.5. Векторное произведение векторов и его свойства.
- •Свойства векторного произведения векторов
- •2.6. Смешанное произведение векторов и его свойства.
- •Тема 8. Комплексные числа и действия с ними.
- •8.2.Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
- •8.3.Тригонометрическая и показательная форма комплексного числа
- •Показательная форма комплексного числа
- •8.4.Возведение комплексных чисел в степень
- •8.5.Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
- •Задание на Дом:
- •Тема 1. Векторная алгебра.
8.5.Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
![]()
два корня:
![]()
![]()
Часто
используется сокращенная запись, оба
корня записывают в одну строчку: ![]() .
.
Такие корни также называют сопряженными комплексными корнями.
Корни извлекаются соответствующим образом:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
т.д.
и
т.д.
Во всех случаях получается два сопряженных комплексных корня.
Задание на Дом:
РЕШИТЬ ЗАДАЧИ (для тех, кто не был на первой лекции и не делал домашнее задание):
Тема 1. Векторная алгебра.
1.Даны
векторы
2.Даны
векторы
Найти
скалярное произведение
3.Даны
векторы
(1;1)
и
(-5;2).
Найти скалярное произведение
|
4.Определить
площадь треугольника, построенного
на векторах
|
5.Определить площадь треугольника, построенного на векторах =(1;2;0), =(2;-1;3). |
6.Определить
объём параллелепипеда, построенного
на векторах
=(-1;1;0),
=(3;1;1),
|
Задачи для самостоятельного решения по теме 8. Комплексные числа.
Найти все комплексные значения
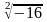 =+-4i
=+-4iНайти все комплексные значения
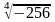 =+-4i
=+-4iНайти все комплексные значения
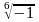 =+-i
=+-iНайти все комплексные значения
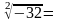
Найти все комплексные значения

Решение квадратных уравнений.
Общая формула вычисления корней:
![]() (1),
(1),
![]()
Найти комплексные корни уравнения
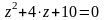
Найти комплексные корни уравнения
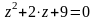
Найти комплексные корни уравнения


 (2;1)
и
(2;1)
и
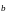 (-1;1).
Найти скалярное произведение
(-1;1).
Найти скалярное произведение

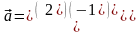 и
и
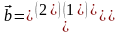 .
.
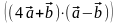
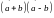
 =(3;2;0),
=(3;2;0),
 =(0;-1;1).
=(0;-1;1).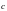 =(0;-1;-2).
=(0;-1;-2).