2.4. Скалярное произведение векторов и его свойства.

Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначение: или .

Таким образом, по определению

, (2.7)

где угол между векторами . По формуле (2.1)

т.е.

(2.8)

Свойства скалярного произведения векторов ( ненулевые векторы)

. прямой угол ( ),

острый угол,

тупой угол;

2^о.

3^о.

4^o.

Произведение называется скалярным квадратом вектора

Скалярное произведение векторов равно сумме попарных произведений соответствующих координат этих векторов:

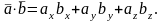(2.9)

Основные приложения скалярного произведения

1. Вычисление угла между векторами Из определения скалярного произведения и формул (2.5), (2.9) следует, что

(2.10)

где угол между векторами .

2. Вычисление проекции одного вектора на другой

Из равенств (2.8) находим:

.

3. Условие перпендикулярности векторов

Используя свойство 1^о и формулу (2.9) , получаем:

2.5. Векторное произведение векторов и его свойства.

Упорядоченная тройка векторов называется правой, если кратчайший поворот первого вектора ко второму виден из конца третьего вектора против часовой стрелки, в противном случае тройка векторов называется левой.

Векторным произведением двух векторов называется третий вектор , удовлетворяющий условиям:

а) длина вектора вычисляется по формуле:

,

где угол между векторами .

Б) вектор перпендикулярен векторам ;

в) тройка векторов правая.

Обозначение: или .

Свойства векторного произведения векторов

1°. – коллинеарные векторы;

2°. ;

3°. ;

4°. .

. (2.11)

Основные приложения векторного произведения.

1. В ычисление площади треугольника (параллелограмма). Из курса математики средней школы известно, что площадь треугольника равна половине произведения его сторон на синус угла между ними, что совпадает с половиной модуля векторного произведения векторов, которые построены на сторонах треугольника. Таким образом,

,

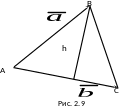
где S площадь треугольника с вершинами в точках А, В, С, (рис. 2.9).

2. Вычисление высоты треугольника (параллелограмма).

Вычислим площадь треугольника двумя способами:

,

где h – высота треугольника, опущенная из вершины В (рис. 2.9). Из этого равенства получаем:

.

Пример. 2.1. Найти площадь треугольника с вершинами в точках А(1, 1, 1), В(1, 2, 3), С(3, 2, 1) и высоту, опущенную из вершины В на сторону АС (рис. 2.9).

Решение. Пусть , тогда

2.6. Смешанное произведение векторов и его свойства.

Пусть – три произвольных вектора.

Три вектора называются компланарными, если они параллельны одной плоскости, т.е., будучи приведены к одному началу, лежат в одной плоскости.

Смешанным произведением векторов называется число равное скалярному произведению векторного произведения векторов на вектор т.е. Геометрический смысл смешанного произведения определяется следующей теоремой.

Теорема 2.1. Смешанное произведение равно объему параллелепипеда V, построенного на векторах , взятому со знаком "+", если тройка векторов правая, и со знаком "–", если тройка векторов левая.

Если векторы компланарны, то смешанное произведение рано нулю, т.е.

Теорема 2.2. В смешанном произведении векторов знаки векторного и скалярного произведений можно поменять местами, т.е.

Так как справедлива теорема 2.2, смешанное произведение обозначают символом .

Найдем выражение смешанного произведения векторов через координаты сомножителей. Пусть

тогда по формулам (2.9), (2.11) находим:

Основные приложения смешанного произведения векторов

1. Вычисление объема тетраэдра (параллелепипеда), построенного на векторах (рис. 2.10).

Если векторы некомпланарны, то по теореме 2.1

. (2.13)

2).Вычисление высоты тетраэдра (параллелепипеда) (рис. 2.10).

Вычислим объем тетраэдра двумя способами:

с одной стороны,

,

с другой стороны,

отсюда (высота параллелепипеда такая же);

3) Условие компланарности векторов (теорема 2.1):

– компланарны.

Ввиду обширности курса и нашего небольшого количества занятий тема, приводимая ниже: Тема 8. Комплексные числа и действия с ними - дается для самостоятельного ознакомления.