25

Мфюа. Маси. Соболева в.В. Линейная алгебра. Лекция 1.

Тема 1. Векторная алгебра.

Системы координат на плоскости. Векторы и линейные операции над ними. Проекция вектора на ось. Разложение вектора на компоненты. Скалярное произведение векторов, его свойства, физический и геометрический смысл. Векторы в пространстве. Векторное произведение векторов, его свойства, физический и геометрический смысл. Смешанное произведение трех векторов, его свойства и геометрический смысл..

Системы координат на плоскости и в пространстве

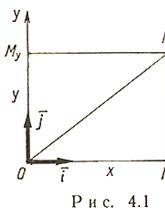
     Системы координат на плоскости       Декартовы прямоугольные координаты (рис. 4.1) 

     О - начало координат, Ох - ось абсцисс, Оy - ось ординат,   - базисные векторы,   - абсцисса точки M (  - проекция точки M на ось Ох параллельно оси Оy),   - ордината точки M (  - проекция точки M на ось Oyпараллельно оси Ox).

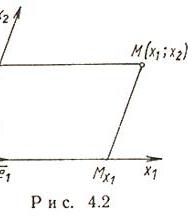
Декартовы косоугольные (афинные) координаты (рис. 4.2)

     О - начало координат,   - оси координат,  ,   - координаты точки M (  - проекция точки M на ось   параллельно оси  , аналогично  ),   - базисные векторы.

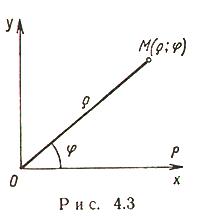
Полярные координаты (рис. 4.3) 

     О - полюс, Ox - полярная ось,   - полярный радиус,   - полярный угол.

     Главные значения   и  :   (иногда  ).

     Выражение декартовых прямоугольных координат через полярные 

     Выражение полярных координат через декартовы прямоугольные 

Системы координат в пространстве       Декартовы прямоугольные координаты (рис. 4.4) 

     О - начало координат, Ох - ось абсцисс, Оy - ось ординат, Оz - ось аппликат,  - базисные векторы. Oxy, Oxz, Oyz - координатные плоскости,   - абсцисса точки M (  - проекция точки M на ось Охпараллельно плоскости Оyz),   - ордината точки M (  - проекция точки M на ось Oy параллельно плоскости Oxz),  - ордината точки M (  - проекция точки M на ось Oz параллельно плоскости Oxy).

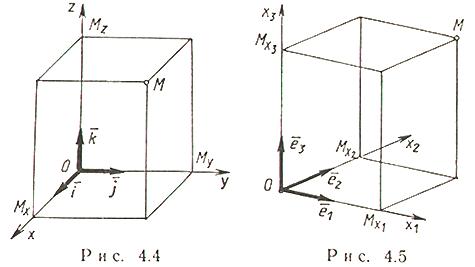
Декартовы косоугольные (афинные) координаты (рис. 4.5)

     О - начало координат,   - оси координат,  ,  ,   - координатные плоскости,  - координаты точки M (  - проекция точки M на ось   параллельно плоскости  ; аналогично  ,  ),   - базисные векторы.

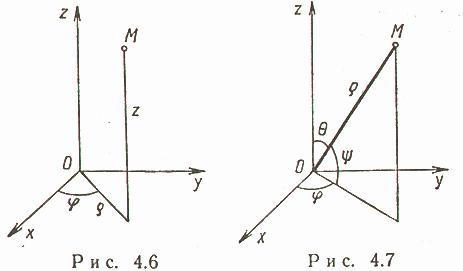
 Цилиндрические координаты (рис. 4.6) 

     Главные значения  ,  ,  : 

     Связь между декартовыми прямоугольными и цилиндрическими координатами:

     Сферические координаты (рис. 4.7) 

     Главные значения  ,  ,  : 

     Иногда вместо   рассматривают  : 

Связь между декартовыми прямоугольными и сферическими координатами

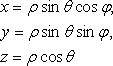   или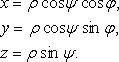   

2. Векторная алгебра

2.1. Понятие вектора. Линейные операции над векторами

Направленный отрезок с началом в точке А и концом в точке В называется геометрическим вектором или просто вектором. Обозначается или строчными буквами латинского алфавита со стрелкой сверху: , …

Длина отрезка АВ называется длиной или модулем вектора и обозначается: .

Если точки А и В совпадают, то вектор называется нулевым. Нулевой вектор обозначается либо , либо 0. Нулевой вектор не имеет направления и длина его равна нулю.

Два вектора называются коллинеарными, если они лежат на одной прямой или параллельны одной прямой (лежат на параллельных прямых).

Два вектора называется равными, если они коллинеарны, имеют одинаковое направление и длину.

Произведением вектора 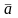на действительное число называется новый вектор , который обладает свойствами:

1^о ;

2 ° направление вектора совпадает с направлением вектора , если (рис. 2.1, а) и противоположно направлению вектора , если (рис. 2.1, б).

Если точка А является началом вектора , то говорят что вектор отложен от точки А. Отложим от точки А вектор , равный . Затем от точки В отложим вектор , равный . Вектор , равный , называется суммой векторов и и обозначается:

Д ля любых трех точек А, В, С (рис. 2.2) справедливо равенство (правило треугольника): .

Умножение вектора на число и сложение векторов называются линейными операциями над векторами.

Два вектора называются противоположными, если их длины равны, и они противоположно направлены. Из определения произведения вектора на число следует, что .

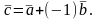Разностью векторов называется вектор , сумма которого с вектором равна вектору . Обозначается: Разность векторов можно определить также равенством: Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.