Задачи к главе 3
Пример 1. Определить интенсивность отказов, среднее время восстановления, среднее время безотказной работы и вероятность безотказной работы в течение 1 года системы, состоящей из 5 последовательно соединенных элементов со следующими показателями надежности:
λ1 = 0,5 год-1; ТВ1 = 16 ч;
λ2 = 0,32 год-1; ТВ2 = 8 ч;
λ3 = 0,3 год-1; ТВ3 = 6 ч;
λ4 = 0,64 год-1; ТВ4 = 12,5 ч;
λ5 = 0,001 год-1; ТВ5 = 15 ч.
Решение. Интенсивность отказов системы, год-1
.
Среднее время восстановления, ч
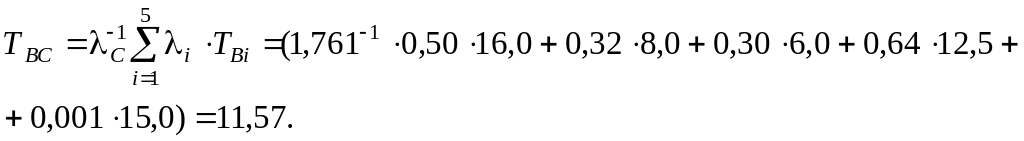
Среднее время безотказной работы, ч
.
Вероятность безотказной работы за t = 1 год
.
Пример 2. Определить приближенно вероятность безотказной работы системы, представленной на рисунке 3.12, методом преобразованием треугольника в звезду.
Вероятности безотказной работы всех элементов одинаковы: pi=p=0,9
2
5
1
Рис. 3.12
Решение.
Образуемый элементами 1, 3, 5 треугольник, преобразуем в звезду с элементами 6, 7, 8 (см. рис.3.13). Согласно формулам (3.18) определим вероятности отказов элементов звезды
6
Рис. 3.13
Используя формулы для последовательно-параллельного соединенных элементов, определяем вероятность безотказной работы системы
3.1
Определить вероятность безотказной
работы в течение 4 лет системы, схема
замещения которой по надежности
представляет собой мостиковую (рис.3.12).
Интенсивность
отказов всех элементов одинакова:
год-1:
|
Рис. 3.14. Мостиковая схема замещения |
3.2. Имеется
система, состоящая из N
= 80 элементов, соединенных логически
последовательно. Параметр потока отказов
системы
ч-1.
С помощью резервирования требуется
обеспечить надежность системы в течение
t
= 2000 ч Ртр(2000)
0,94.
3.3.
Система состоит из трех устройств.
Интенсивность отказов электронного
устройства равна
1/ч
= const.
Интенсивности отказов двух
электромеханических устройств линейно
зависят от времени и определяются
следующими формулами
1/ч;
1/ч.
Необходимо рассчитать вероятность безотказной работы изделия в течение 100 ч.
3.4. Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента ti = 1000 ч. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти среднее время безотказной работы системы Т, а также частоту отказов а(t) и интенсивность отказов λС(t) в момент времени t = 50 ч в следующих случаях:
а) нерезервированной системы,
б) дублированной системы при постоянно включенном резерве.
3.5. Нерезервированная система управления состоит из n = 5000 элементов. Для повышения надежности системы предполагается провести общее резервирование элементов. Чтобы приближенно оценить возможность достижения заданной вероятности безотказной работы системы РС(t) = 0,9 при t =10 ч, необходимо рассчитать среднюю интенсивность отказов одного элемента при предположении отсутствия последействия отказов.
3.6. Нерезервированная система управления состоит из n = 4000 элементов. Известна требуемая вероятность безотказной работы системы РС(t) = 0,9 при t = 100 ч. Необходимо рассчитать допустимую среднюю интенсивность отказов одного элемента, считая элементы равнонадежными, для того чтобы приближенно оценить достижение заданной вероятности безотказной работы при отсутствии профилактических осмотров в следующих случаях:
а) резервирование отсутствует;
б) применено общее резервирование.
3.7. Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента ti = 1000 ч. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти вероятность безотказной работы системы РС(t), среднее время безотказной работы системы T, а также частоту отказов а(t) и интенсивность отказов λС(t) в момент времени t = 50 ч в следующих случаях:
а) нерезервированной системы,
б) системы при включении резерва по способу замещения (ненагруженный резерв).
3.8. Вероятность безотказной работы преобразователя постоянного тока в переменный в течение времени t = 1000 ч равна 0,95, т. е. Р(1000) = 0,95. Для повышения надежности системы электроснабжения на объекте имеется такой же преобразователь, который включается в работу при отказе первого (режим ненагруженного резерва). Требуется рассчитать вероятность безотказной работы и среднее время безотказной работы системы, состоящей из двух преобразователей, а определить интенсивность отказов λС (t) системы.
3.9.
Передающее устройство состоит из одного
работающего передатчика (
1/ч)
и одного передатчика в облегченном
резерве (
1/ч).
Требуется определить вероятность
безотказной работы устройства
,
среднее время безотказной работы
устройства Т.
Определить
при t
= 20 ч.
3.10. Устройство автоматического поиска неисправностей состоит из двух логических блоков. Среднее время безотказной работы этих блоков одинаково и для каждого из них равно Т = 200 ч. Требуется определить среднее время безотказной работы устройства Т для двух случаев:
а) имеется ненагруженный резерв всего устройства;
б) имеется ненагруженный резерв каждого блока.
3.11.
Нерезервированная система управления
состоит из n
= 5000 элементов. Для повышения надежности
системы предполагается провести
раздельное резервирование элементов.
Чтобы приближенно оценить возможность
достижения заданной вероятности
безотказной работы системы
при t
= 10 ч, необходимо рассчитать среднюю
интенсивность отказов одного элемента
при предположении отсутствия последействия
отказов.
3.12. Нерезервированная система управления состоит из n = 4000 элементов. Известна требуемая вероятность безотказной работы системы при t = 100 ч. Необходимо рассчитать допустимую среднюю интенсивность отказов одного элемента, считая элементы равнонадежными, для того чтобы приближенно оценить достижение заданной вероятности безотказной работы при отсутствии профилактических осмотров в следующих случаях:
а) резервирование отсутствует;
б) применено раздельное (поэлементное) резервирование.
3.13.
В радиопередатчике, состоящем из трех
равнонадежных каскадов (
)
применено раздельное дублирование
каждого каскада. Интенсивность отказов
каскадов равна
1/ч. Рассчитать вероятность безотказной
работы
в течение времени t
= 100 ч и среднее время безотказной работы
mtc
радиопередатчика.
3.14.
Для повышения точности измерения
некоторой величины применена схема
группирования приборов из пяти по три,
т.е. результат измерения считается
верным по показанию среднего (третьего)
прибора. Требуется найти вероятность
безотказной работы
,
среднее время безотказной работы Т
такой системы, а также и интенсивность
отказов
системы, если интенсивность отказов
каждого прибора
1/ч.
3.15.
Интенсивность отказов измерительного
прибора
1/ч.
Для повышения точности измерения
применена схема группирования из трех
по два (
).
Необходимо определить вероятность
безотказной работы схемы
,
среднее время безотказной работы схемы
Т,
интенсивность отказов
схемы.
3.16.
Интенсивность отказов измерительного
прибора
1/ч. Для повышения
точности измерения применена схема
группирования из пяти по три (
).
Необходимо определить вероятность
безотказной работы схемы
,
интенсивность отказов
схемы.
3.17.
Блок телеметрии включает в себя два
одинаковых приемника. Интенсивность
отказов каждого приемника составляет
1/ч.
Имеется один приемник в ненагруженном
скользящем резерве. Определить вероятность
безотказной работы
резервированной системы, среднее время
безотказной работы Т
системы, интенсивность отказов
.
Определить
при t = 250
ч.
Определить
,
когда резерв отсутствует.
3.18.
Радиорелейная станция содержит два
приемопередатчика, один из которых
используется по назначению, а второй
находится в ненагруженном резерве.
Определить среднее время безотказной
работы станции Т
при условии,
что для каждого приемопередатчика
1/ч;
1/ч.
3.19. Предлагается вариант структурной схемы объекта в смысле надежности и исходные параметры. Для заданного варианта структурной схемы объекта определить аналитические соотношения для расчета показателей надежности: вероятность безотказной работы; вероятность отказа; среднюю наработку на отказ. Построить графики функций P(t), Q(t), (t).
3.20. За наблюдаемый период эксплуатации в аппаратуре было зафиксировано 8 отказов. Время восстановления составило:
t1 = 12 мин, |
t2 = 23 мин, |
t3 = 15 мин, |
t4 = 9 мин, |
t5 = 17 мин, |
t6 = 28 мин, |
t7 = 25 мин, |
t8 = 31 мин |
3.21.
Интенсивность отказов
в одной из подсистем автоматизированной
системы обработки информации и управления
(АСОИУ), которая представляет собой
сложную восстанавливаемую систему,
есть величина постоянная и равная 0,015
1/ч. Среднее время восстановления равно
100 ч. Необходимо вычислить вероятность
застать систему в исправном состоянии
в момент времени t
= 10 ч.
3.22. Коэффициент готовности одной из подсистем АСОИУ, которая представляет собой сложную восстанавливаемую систему, равен 0,9. Среднее время ее восстановления составляет 100 ч. Требуется найти вероятность застать систему в исправном состоянии в момент времени t = 12 ч.
3.23.
В процессе эксплуатации 100 восстанавливаемых
изделий возникали отказы, которые
фиксировались в интервалах времени
= 100 ч. Число отказов п
за
время эксплуатации в течение 1000 ч
приведено в табл. 3.1. Требуется определить
вероятность безотказной работы изделий
в течение 1000 ч, вычислить интенсивность
отказов и построить график.
Таблица 3.1
Число отказов за время эксплуатации
|
0…100 |
101…200 |
201…300 |
301…400 |
401…500 |
n |
2 |
4 |
6 |
7 |
8 |
, ч |
501…600 |
601…700 |
701…800 |
801…900 |
901…1000 |
n |
9 |
9 |
10 |
10 |
10 |
,
ч
3.24. При увеличении напряжения в два раза может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов соответственно с вероятностями 0,3, 0,4 и 0,6. Определить вероятность того, что при этом не будет разрыва цепи. Как изменится искомая вероятность, если не будет первого элемента?
3.25. Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до наступления события. Определить вероятность того, что придется проводить четвертый опыт.
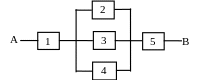
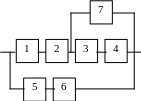
3.26. Электрическая цепь между точками А и В составлена по схеме, которая представлена на рис. 3.13. Выход из строя за время t различных элементов цепи − независимые события, имеющие следующие вероятности:
Номер элемента |
1 |
2 |
3 |
4 |
5 |
Вероятность выхода из строя |
0,6 |
0,5 |
0,4 |
0,7 |
0,9 |
Определить вероятность разрыва цепи.
|
|
Рис. 3.15. Схема электрической цепи к вопросу 3.25 |
Рис. 3.16. Схема электрической цепи к вопросу 3.26 |
3.27. Разрыв электрической цепи может произойти вследствие выхода из строя элемента К или двух элементов К1, и К2, (рис. 3.14). Вероятность выхода из строя элемента К равна 0,3, а для каждого из элементов К1 и К2 эти вероятности равны 0,2. Определить вероятность разрыва электрической цепи.
3.28. Имеется вариант структурной схемы объекта в смысле надежности и исходные параметры, характеризующие свойства элементов исследуемого объекта, определить:
а) для заданного варианта структурной схемы объекта показатели надежности P(t), Q(t), T, l(t).
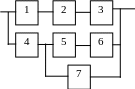
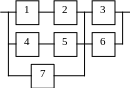
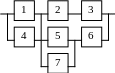
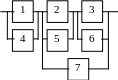
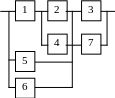
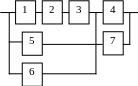
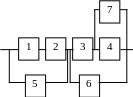
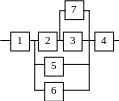
б) построить графики функций P(t), Q(t), l(t).
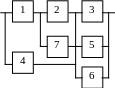
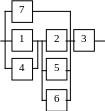
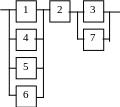
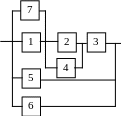
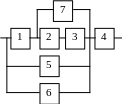
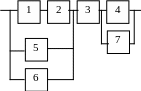
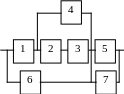
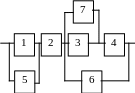
Варианты структурных схем объектов с
последовательно-параллельным соединением элементов
|
|
|
|
В1 |
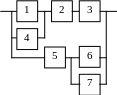
В2 |
|
|
|
|
|
|
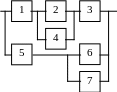
В3 |
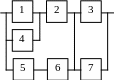
В4 |
|
|
|
|
|
|
В5 |
В6 |
|
|
|
|
В7 |
В8 |
|
|
|
|
|
|
В9 |
В10 |
|
|
|
|
|
|
В11 |
В12 |
|
|
|
|
|
|
В13 |
В14 |
|
|
|
|
В15 |
В16 |
|
|
|
|
|
|
В17 |
В18 |
|
|
|
|
|
|
В19 |
В20 |
Таблица 3.2
Варианты численных значений интенсивностей отказов
отдельных элементов
Номер варианта |
Интенсивности отказов элементов, i10-61/час |
||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
1 |
4 |
7 |
3 |
2 |
6 |
5 |
2 |
6 |
2 |
1 |
5 |
3 |
4 |
7 |
Окончание табл. 3.2
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
3 |
7 |
5 |
2 |
4 |
6 |
1 |
3 |
4 |
3 |
6 |
4 |
7 |
5 |
2 |
1 |
5 |
5 |
3 |
6 |
1 |
4 |
7 |
2 |
6 |
8 |
7 |
10 |
6 |
9 |
12 |
11 |
7 |
12 |
9 |
8 |
11 |
7 |
11 |
6 |
8 |
11 |
10 |
7 |
9 |
12 |
6 |
8 |
9 |
9 |
6 |
12 |
8 |
11 |
10 |
7 |
10 |
7 |
12 |
9 |
10 |
6 |
8 |
11 |
11 |
10 |
13 |
14 |
15 |
12 |
11 |
9 |
12 |
14 |
15 |
10 |
9 |
13 |
12 |
11 |
13 |
12 |
10 |
11 |
13 |
14 |
9 |
15 |
14 |
11 |
9 |
13 |
12 |
10 |
15 |
14 |
15 |
14 |
13 |
9 |
11 |
12 |
10 |
15 |
16 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
17 |
5 |
11 |
9 |
1 |
13 |
7 |
3 |
18 |
9 |
1 |
7 |
3 |
5 |
13 |
11 |
19 |
7 |
5 |
1 |
11 |
9 |
3 |
13 |
20 |
11 |
13 |
9 |
5 |
1 |
7 |
3 |