3. Надежность взаимосвязанных элементов
3.1. Надежность систем с последовательным соединением элементов
Реальные объекты системы электроснабжения в большинстве случаев состоят из совокупностей взаимосвязанных элементов.
Последовательным (основным) соединением элементов в смысле надежности называется такое соединение, при котором выход из строя бы одного из них приводит к отказу всю систему, т.е. последовательная структура работоспособна, если все ее элементы работоспособны.
В производственной системе элементы физически могут быть соединены параллельно, однако с позиций надежности они могут быть соединяться как параллельно, так и последовательно.
Схема замещения (по надежности) системы с последовательной структурой представлена на рис. 3.1.
|
Рис. 3.1. Схема замещения системы с последовательной структурой |
Отказы элементов этой модели являются независимыми и несовместными событиями, которые приводят к полной потере работоспособности всю систему. Вероятность безотказной работы последовательной структуры будет определяться по теореме умножения вероятностей: вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий
,
(3.1)
где Рi(t) – вероятность работы i-го элемента, п – число элементов.
Вероятность отказа последовательной структуры
,
(3.2)
где Qi – вероятность отказа i-го элемента.
Если все элементы
структуры равнонадежны, т.е.
,
,
то формулы (3.1) и (3.2) принимают вид:
,
(3.3)
.
(3.4)
Вероятность безотказной работы, для экспоненциального закона распределения времени, при постоянной во времени интенсивности отказов каждого элемента, будет определяться по формуле:
,
(3.5)
Интенсивность отказов системы с последовательной структурой в целом можно определить по формуле:
.
(3.6)
Среднее время безотказной работы системы:
.
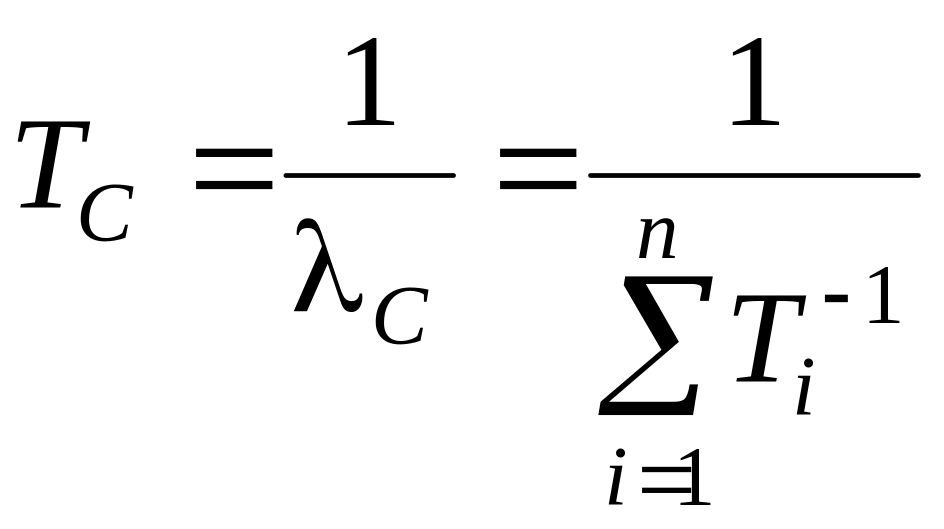(3.7)
где Тi – среднее время безотказной работы i-го элемента.
Среднее время восстановления системы
,
(3.8)
где ТBi – время восстановления i-го элемента, является математическим ожиданием времени восстановления, взвешенным по интенсивности отказов п последовательно соединенных элементов.
3.2. Надежность систем с параллельным соединением элементов
Отказы элементов в такой модели можно рассматривать как независимые и совместные события, приводящие к частичной или полной потере работоспособности объекта.
Параллельным соединением элементов в смысле надежности называется структура, отказ которой наступает при отказе всех элементов, входящих в нее. Параллельную структуру называют также избыточной или резервированной, поскольку она содержит элементов больше, чем это необходимо для ее нормальной работы. При отказе одного или нескольких элементов функция структуры выполняется оставшимися в работе элементами, если последние удовлетворительно выполняют функции отказавших.
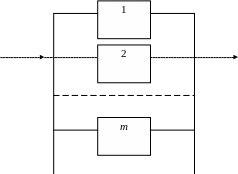
Схема замещения (по надежности) системы с параллельной структурой представлена на рис. 3.2.
|
Рис. 3.2. Схема замещения системы с параллельной структурой |
В общем случае отказ параллельной структуры предполагает, что все т элементов находятся в состоянии простоя, т. е.
.
(3.9)
Вероятность безотказной работы системы
.
(3.10)
При равнонадежных
элементах
,
имеем
,
(3.11)
.
(3.12)
Как и для систем с последовательным соединением элементов, здесь предполагается независимость отказов всех элементов. Кроме того, пропускная способность элементов не ограничивается.
Число параллельно
соединенных элементов в СЭС редко бывает
больше трех. Вероятность того, что будут
работать один или два элемента (при
),
будет в соответствии с формулой (3.1)
равна
.
(3.13)
Вероятность отказа обоих элементов
.
(3.14)
Интенсивность отказа системы, состоящей из двух параллельно соединенных элементов, будет определяться по формуле /9/:
,
а среднее время безотказной работы:
.
Кроме последовательного и параллельного соединения элементов, в теории надежности используют понятие смешанного соединения элементов, которое представляет одну или несколько комбинаций логического последовательного и параллельного соединения элементов. Определение показателей надежности таких структур производится методом свертки, т.е. поэтапным эквивалентированием элементов по формулам для последовательного и параллельного соединений.