Расчет статически неопределимой фермы за пределами упругости. Условие:

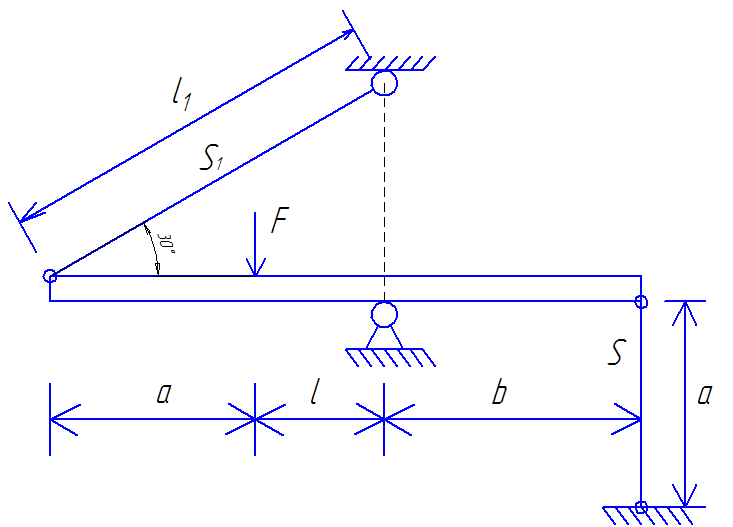
Раскрыть статическую неопределимость и вычислить допустимое значение нагрузки F из расчета на прочность по допускаемым напряжениям.

Принять: l = 50 см;; a/l = 1,5; b/l = 2,0; S₁/S = 1,0

Решение:

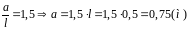
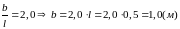
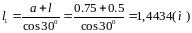
Первоначально произведем расчет в упругой стадии, используя для этого метод сил

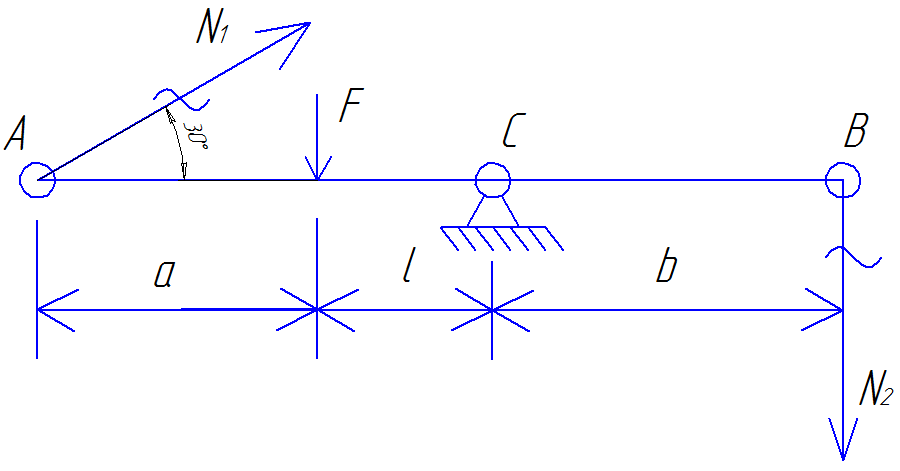
Составим уравнения равновесия статики для балки AB, введя в рассмотрение усилия в стержнях № 1 и 2:

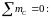
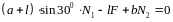
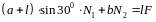
Подставив числовые значения, получим:

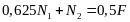(1)

Задача один раз статически неопределима. Дополнительное уравнение получим, рассмотрев геометрическую картину перемещений.

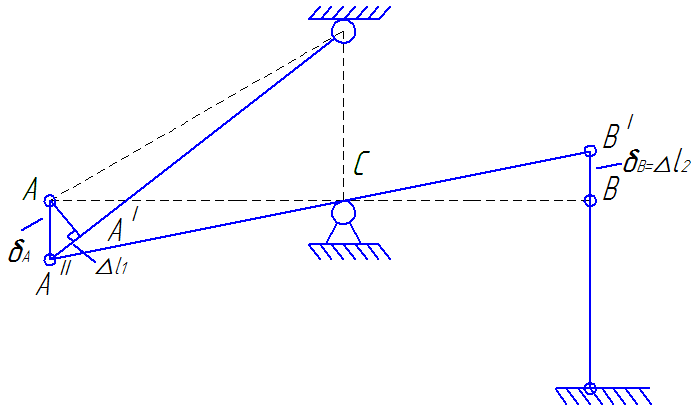
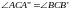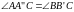Рассмотрим ΔАA”C и ΔBB’C. Эти треугольники будут подобны по трем углам ( - накрест лежащие, - накрест лежащие, 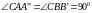). Следовательно, ΔАA”C и ΔBB’C подобны по первому признаку (по трем углам).

Следовательно,

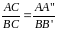
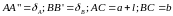
Отсюда,

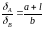
Подставив числовые значения, получим:

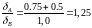
С другой стороны, ;

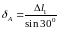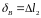
Следовательно,

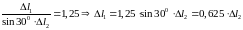
Уравнение совместимости деформации записываем в физической форме:

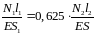
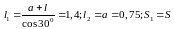
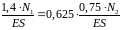
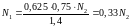(2)

Решаем систему уравнений (1) и (2):

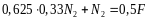
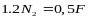
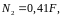
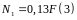
Наибольшее усилие возникает во втором стержне. Приравнивая его 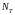, получим:

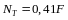
Откуда 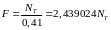(4).

Подставляя (4) в (3), получим усилия в стержнях при текучести второго стержня:

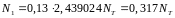
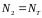
_{Занесем эти усилия в таблицу 1 в столбец «Первый шаг»}

Таблица 1. Шаговый процесс расчета.

Усилия	Первый шаг	Приращение после первого шага	Второй шаг	Остаточные значения
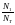
	0,317	0,683	1,0	0,583
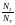
	1,0	0,0	1,0	-0,315
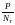
	2,439	0,85375	3,54	0,0

Далее переходим ко второму шагу и произведем расчет системы, изображенной на рисунке, в упругой стадии

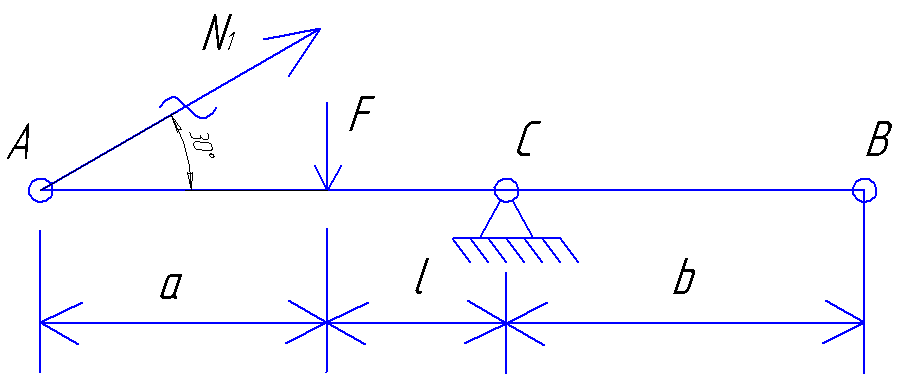
Система является статически определимой и для ее расчета составим сумму моментов относительно точки С:

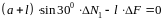
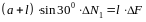
Подставив числовые значения, получим:

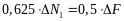
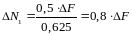
_{Складывая это усилие с усилием первого шага, получим:}

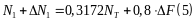
_{Такое сложение возможно, так как усилие во втором стержне при росте внешней силы будет оставаться постоянным и играть роль нагрузки для системы, состоящей из двух стержней. Приравнивая выражение (5) значению NT и решая его относительно ΔF, получим}

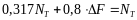
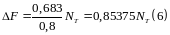
_{Подставляя (6) в (5), получим усилия второго шага}

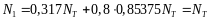
_{Предельная сила равна:}

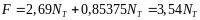
Результаты заносим в таблицу 1.

Произведем разгрузку системы. При разгрузке система ведет себя как упругая:

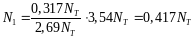
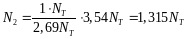
_{В ычитая эти значения из соответствующих усилий второго шага, получим их остаточные значения:}

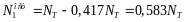
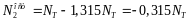
_{Вновь нагрузим систему нагрузкой F=3,54NT и вычислим усилия и вычислим усилия и перемещения с учетом их остаточных значений:}

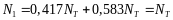
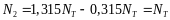
_{Таким образом, система «приспособилась» к нагрузке, т.е. при нагрузке не более F=3,54NT , она работает как упругая.}