МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ ГОСУДАРСТВЕННОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ-

УЧЕБНО-НАУЧНО-ПРОИЗВОДСТВЕННЫЙ КОМПЛЕКС»

Кафедра: «Динамика и прочность машин»

Расчетно-графическая работа

по дисциплине «Прикладная механика»

по теме «Расчет статически неопределимых систем»

Работу выполнил студент Гуров Михаил Юрьевич

Шифр 140400 Группа 31-ЭО Факультет НТ и АП

Специальность Электроэнергетика

Курсовая работа защищена с оценкой _________________________

Руководитель ____________ Малинин Георгий Владиславович

подпись

Орел 2013 г.

Содержание

Задача 1.Расчет задачи методом упругой линии

Задача 2.Расчет задачи методом Мора

Задача 3. Расчет статически неопределимой балки

Задача 4. Расчет статически неопределимой рамы

Задача 5. Расчет статически неопределимой фермы за пределами упругости

_{Задача 6. Расчет статически неопределимой балки методом конечных элементов.}

Список используемой литературы

Задача 1 Задача 1. Определение перемещений методом упругой линии.

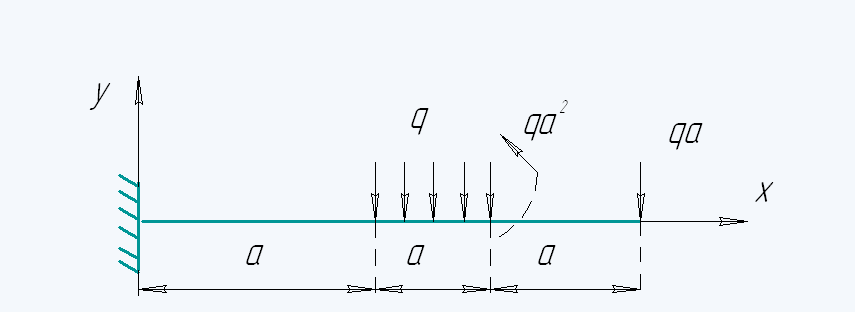
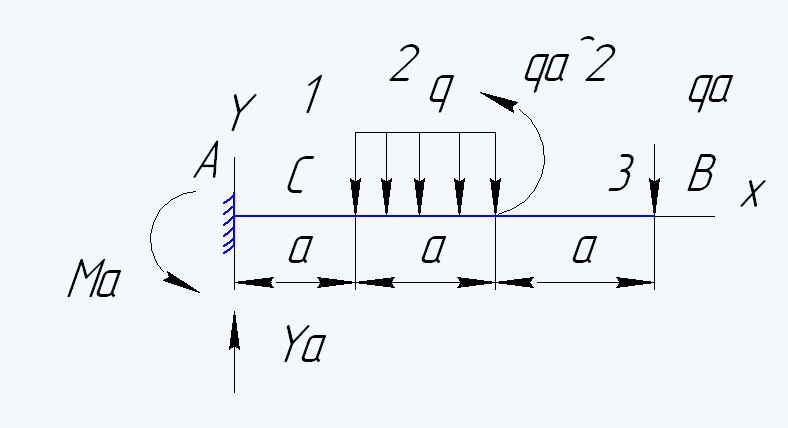
Определим опорные реакции балки

∑Y=0 Y_a-qa-qa=0

Y_a=2qa

∑M_a=M_a-q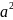 +qa*3a+qa* 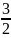a=0

M_a=-3.5q

Для проверки правильности определения опорных реакций составим уравнение равновесия.

∑M_c=0, следует -3.5q +q +qa*2a+qa*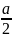 -2.5q +2.5q =0

Реакции найдены правильно.

Применение метода начальных параметров. Для нашего случая запишем

EJ_ty(x)=EJ_zy₀+θ₀x+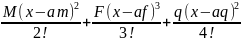

Граничные условия:

;

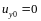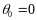
Разделим балку на участки и распишем каждый участок с применением метода сил.

EJ_ty(x)=-3.5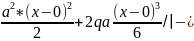q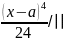` q -q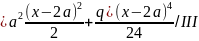

_{С помощью уравнения упругой линии построим эпюру перемещений:}

Участок 1(0≤ x ≤ a):

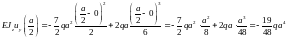
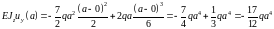
Участок 2(0≤ x ≤ a):

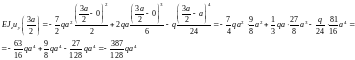
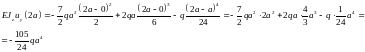Участок 3(0≤ x ≤ a):

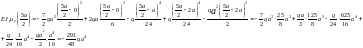
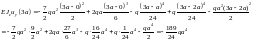
Строим эпюру перемещений:

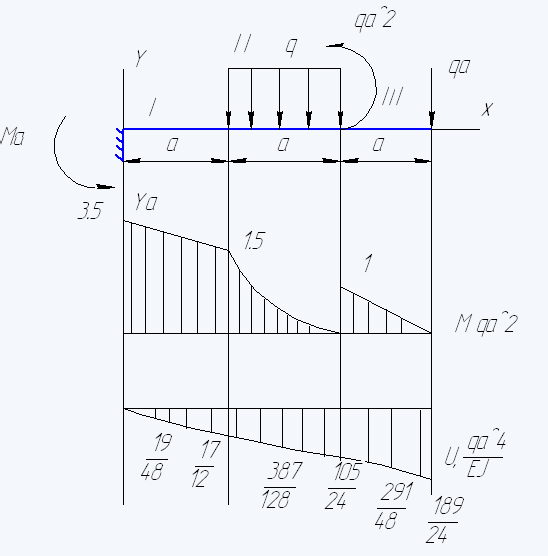
Задача 2

Расчет задачи методом Мора.

Разделим балку на участки, рассмотрим каждый участок и построим эпюру моментов.

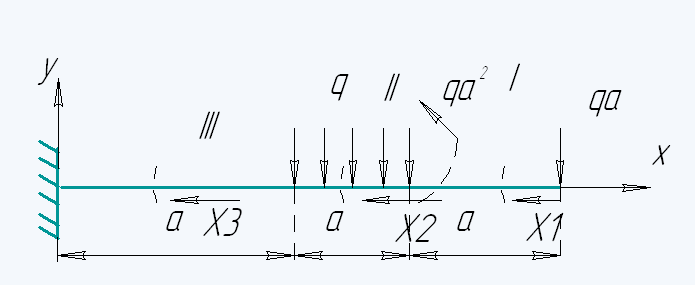
Участок 1:

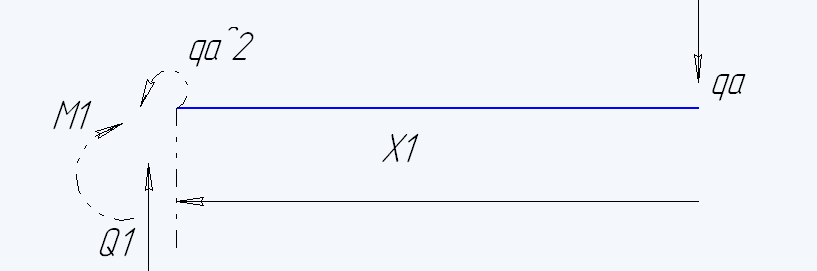
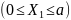
M_x^I=qa*X₁ M₀^I(0)=0 M_a^I( )=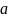

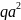
Участок 2:

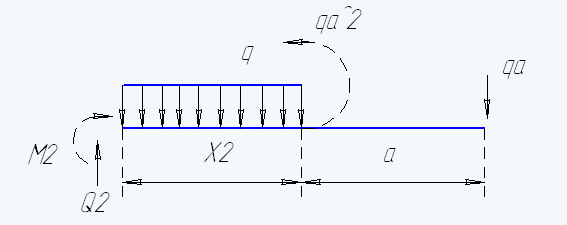
M_x^II=10*(a+X₂)-10+10*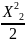

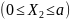
M₀^II(0)= - =0

M_a^II(a)=2 - + *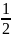 =2 - +0.5 =1.5

Участок 3:

M_x^III=qa*(2a+X₃)-q +qa*( +X₃) )

M₀^III(0)=0.15

M_a^III(a)= *2+ - + *0.15=3 - + *0.5+ =3.5

Строим эпюру моментов и единичную эпюру .

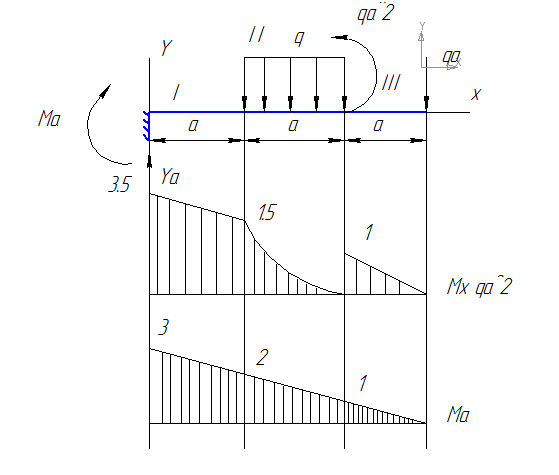
Находим перемещения каждого участка балки:

Сделаем перемножение эпюр по методу Симпсона ,для этого запишем формулу.

Δ=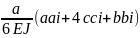

Найдем Δ∣

Δ∣=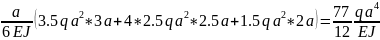

Найдем середину параболы эпюры моментов на участке ∣∣ .

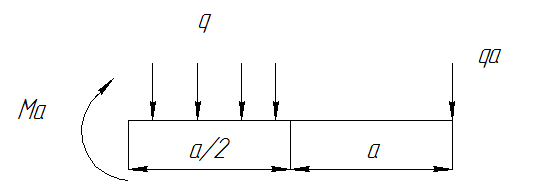
M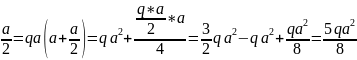

Найдем Δ∣∣

Δ∣∣=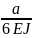 (1.5q =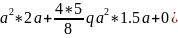

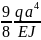
Найдем Δ∣∣∣

Δ∣∣∣= (q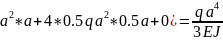

Находим суммарное перемещение всей балки:

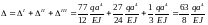
Построим эпюру перемещений графическим способом. Для этого будем прикладывать единичные силы в точки, перемещения которых надо определить (a/2, a, 3a/2, 2a, 5a/2, 3a):

Для точки а/2:

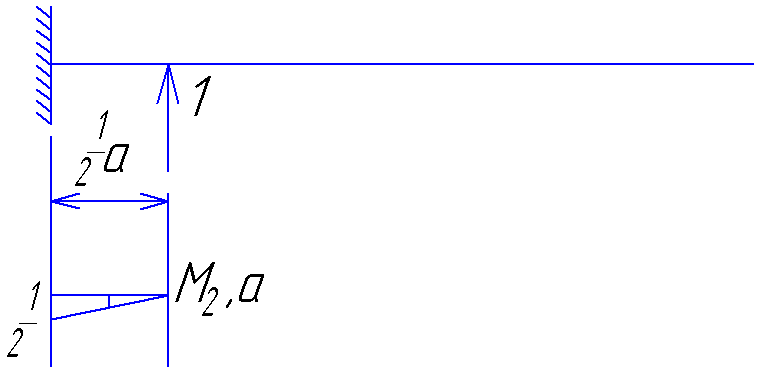
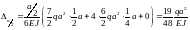
Для точки а:

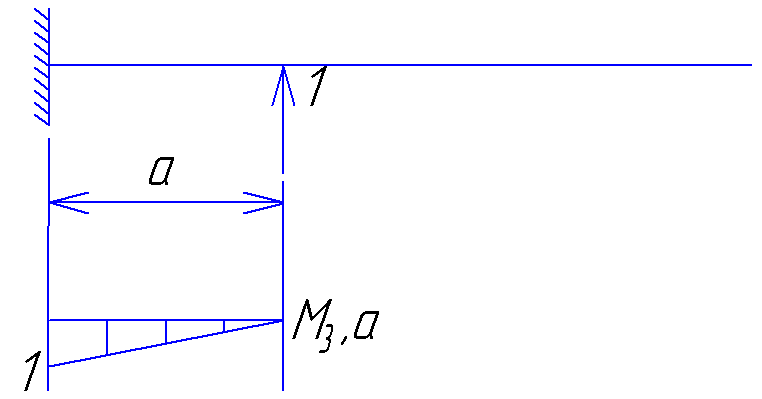
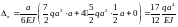
Для точки 3а/2:

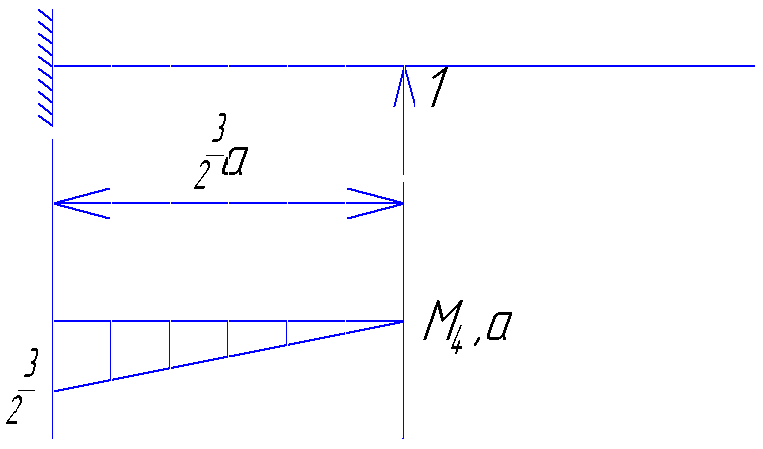
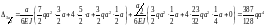
Для точки 2а:

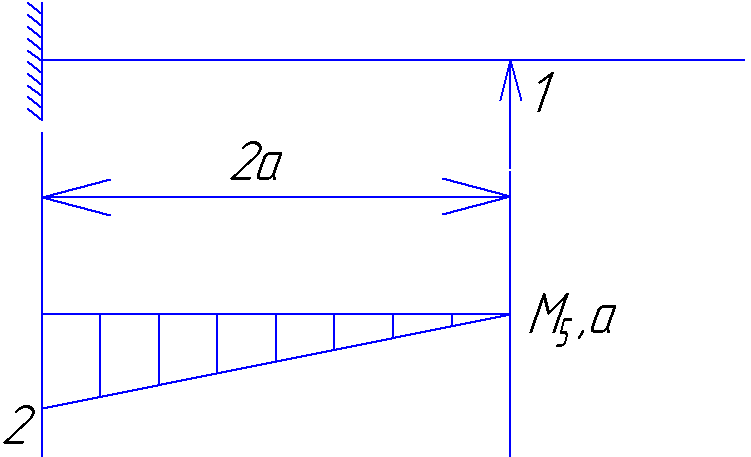
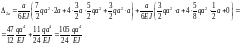
Для точки 5а/2:

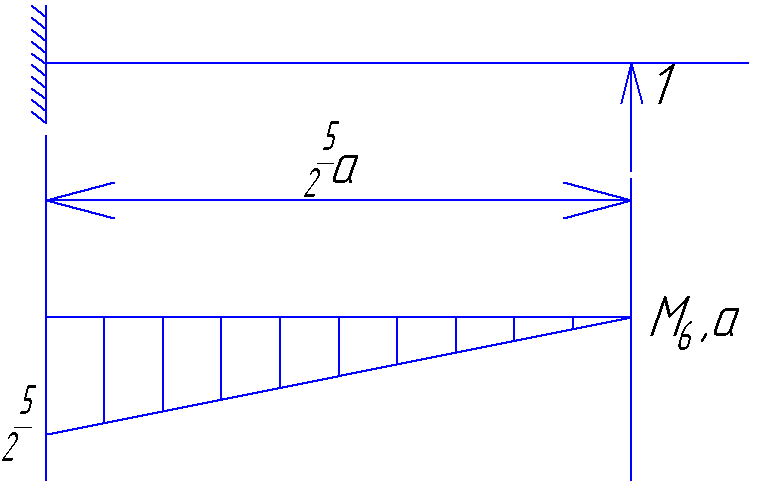
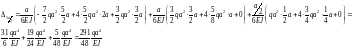Для точки 3а:

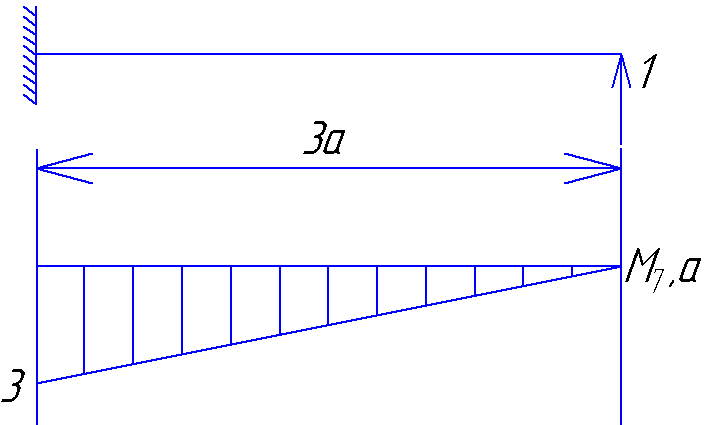
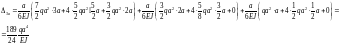
По полученным значениям построим эпюру перемещений

Задача номер 3

Условие задачи.

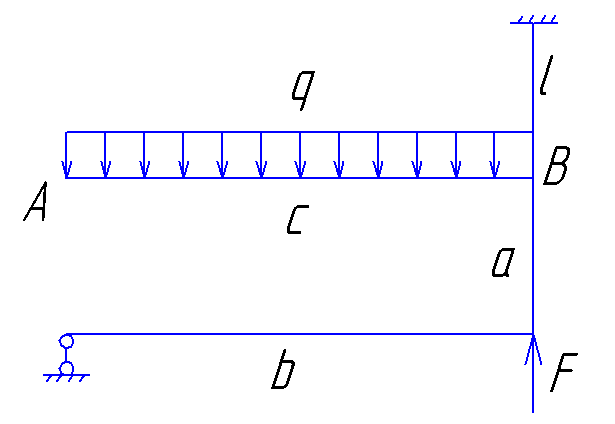
Для плоской статически неопределимой рамы квадратного поперечного сечения (сторона квадрата h) требуется:

1. раскрыв статическую неопределимость, построить эпюры изгибающего момента, продольных и поперечных сил и выполнить деформационную проверку правильности раскрытия статической неопределимости;

2. из расчета на прочность найти допустимое значение параметра нагрузки q;

3. определить горизонтальное перемещение сечения A и угол поворота (в град) сечения в точке B.

Принять: h=8мм; l=0,4м; материал – сталь Ст.3; [n] = 2; a/l = 1,0; b/l = 2,0; c/l = 2,0;F/ql = 2,0.