МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Рыбинская государственная авиационная технологическая

академия им. П.А. Соловьева

Факультет радиоэлектроники и информатики

Кафедра радиоэлектронных и телекоммуникационных систем

КУРСОВАЯ РАБОТА

по дисциплине

основы радиоэлектроники и связи

Вариант № 676

Исполнитель: студент гр. шифр подпись “___”_________200__ г.

Раков А.С.

Руководитель: подпись “___”_________200__ г.

Кругликов С.Ю.

Рыбинск 2013

Рыбинская государственная авиационная технологическая академия им. П.А. Соловьева Факультет радиоэлектроники и информатики
Кафедра радиоэлектронных и телекоммуникационных систем
Р Е Ц Е Н З И Я
на курсовую работу по дисциплине основы радиоэлектроники и связи
С Т Р У К Т У Р А К У Р С О В О Й Р А Б О Т Ы
– Титульный лист
– Рецензия
– Решение задания 1 (1)
– Решение задания 2 (2)
– Решение задания 3 (3)
– Решение задания 4 (4)
– Решение задания 5 (5)
– Решение задания 6 (6)
– Решение задания 7 (7)
– Решение задания 8 (8)
– Литература
Р Е З У Л Ь Т А Т Ы Р Е Ц Е Н З И Р О В А Н И Я
Параметры оценки		Показатели ответов студента, %									Итого, %
		1	2	3	4	5		6	7	8
Соответствие заданию
Общая грамотность
Объем расчетов
Корректность расчетов
Итоговая оценка, %		 – зачтено  – не зачтено  – зачтено повторно
Дата выдачи заданий курсовой работы:							“____” ___________ 200__ г.
Дата сдачи курсовой работы на проверку:							“____” ___________ 200__ г.
Дата возвращения работы для исправлений:							“____” ___________ 200__ г.
Дата повторной сдачи работы на проверку:							“____” ___________ 200__ г.
Подпись преподавателя:

Задание на курсовую работу

Рассчитываемые характеристики

1. Корреляционная функция для входного сигнала.

2. Спектральная плотность входного сигнала, амплитудный и фазовый спектр, ширина спектра.

3. Частотный коэффициент передачи цепи, АЧХ, ФЧХ.

4. Импульсная и переходная характеристики цепи.

5. Спектральная плотность выходного сигнала, амплитудный и фазовый спектр, ширина спектра.

6. Выходной сигнал.

Исходные данные

Схема электрическая принципиальная:

Входной сигнал:

u_вх(t)

U

0

T

t

Параметры элементов цепи и сигнала:

Вариант	Параметры
6	C C1,нФ	3
	C C2,нФ	2
	L L1 мГн	1
	L L2,мГн	2
	R1,кОм	2
	R2,кОм	3
	U,В	5
	Е T,мкс	10

1. Нахождение корреляционной функции для входного сигнала, сдвинутого на на интервале

При обработке сигналов часто приходится сравнивать сигнал со смещёнными во времени копиями этого сигнала, а также другими сигналами. О степени связи сигнала со смещёнными копиями можно судить по корреляционным функциям. Для вещественного сигнала S(t), имеющего конечную энергию на бесконечном интервале времени автокорреляционная функция определяется следующим образом:

(1.1)

где -интервал сдвига функции.

При таком определении автокорреляционная функция (АКФ) имеет размерность энергии.

В нашем случае мы имеем сигнал треугольной формы, представленный на рис 1.1.

u

t

T

Рис.1.1 Исходный сигнал.

Математически исходный сигнал можно записать:

τ

Рис.1.2 Смещенный во времени сигнал

Корреляционная функция для входного сигнала, сдвинутого на на интервале [τ, T], согласно (1.1) определяется следующим образом:

(1.2)

где  ( ) - единичная функция

График корреляционной функции (1.2) представлен на рис.1.3

Рис.1.3 Корреляционная функция входного сигнала

Нахождение интервала корреляции:

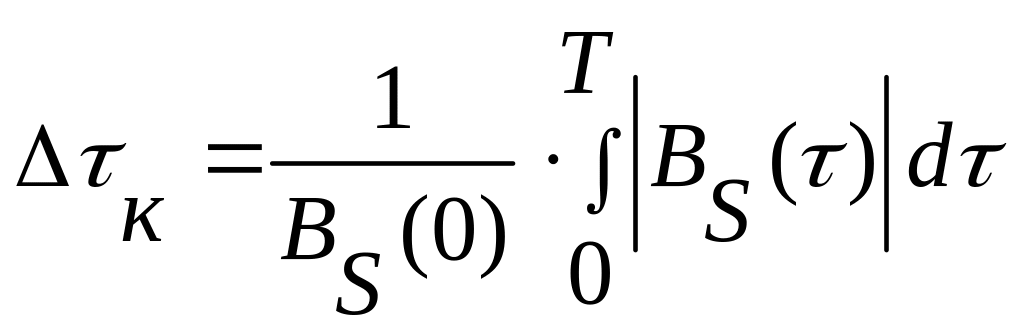(1.3)

(1.4)

(1.5)

Подставляя (1.4) и (1.5) в (1.3), найдем значение интервала корреляции:

2. Спектральный анализ входного сигнала

2.1 Спектральная плотность входного сигнала

(2.1.1)

Данная функция является спектральной плотностью сигнала s(t). Формула (2.1.1) осуществляет преобразование Фурье данного сигнала. Спектральная плотность - комплекснозначная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе элементарных синусоид. Модуль спектральной плотности есть амплитудный спектр сигнала, а ее аргумент - фазовый спектр.

Запишем математическое выражение для входного сигнала, используя единичную функцию :

(2.1.2)

График входного сигнала представлен на рис. 2.1

Рис.2.1 Входной сигнал

Представим сигнал в операторной форме. При нахождении изображения сигнала по Лапласу необходимо учитывать свойство временного сдвига:

(2.1.3)

При этом изображения простых сигналов определяются как:

(2.1.4)

Применяя свойство линейности и временного сдвига (2.1.3), а также, учитывая (2.1.4) найдем изображение нашего сигнала:

(2.1.5)

Так как площадь фигуры, ограниченной графиком функции s(t) и осью абсцисс, является конечной величиной, сигнал s(t) – абсолютно интегрируемый, следовательно, для перехода от изображения к спектральной плотности достаточно заменить p на jω.

Заменив p на jω, получим:

Для преобразования используем формулу Эйлера (2.1.6):

(2.1.6)

Тогда

(2.1.7)