§ 11 Кольца. Поля Кольца

Кольцом называется (непустое) множество , на котором определены две операции (сложение + и умножение  ), обладающие следующими свойствами:

1.Множество относительно операции сложения образует коммутативную группу с нейтральным элементом 0.

2.Операция умножения ассоциативна: для любых .

3.В множестве K существует мультипликативная единица e  0, т.ч. a  e = e  a.

4.Операции сложения и умножения подчиняются дистрибутивному закону:

для любых .

При этом множество , рассматриваемое лишь относительно операции сложения, называется аддитивной группой кольца.

Примеры колец.

Множество целых чисел с операциями сложения и умножения – кольцо целых чисел Z

1. Множество многочленов от одного неизвестного с действительными коэффициентами с операциями сложения и умножения многочленов – кольцо многочленов .

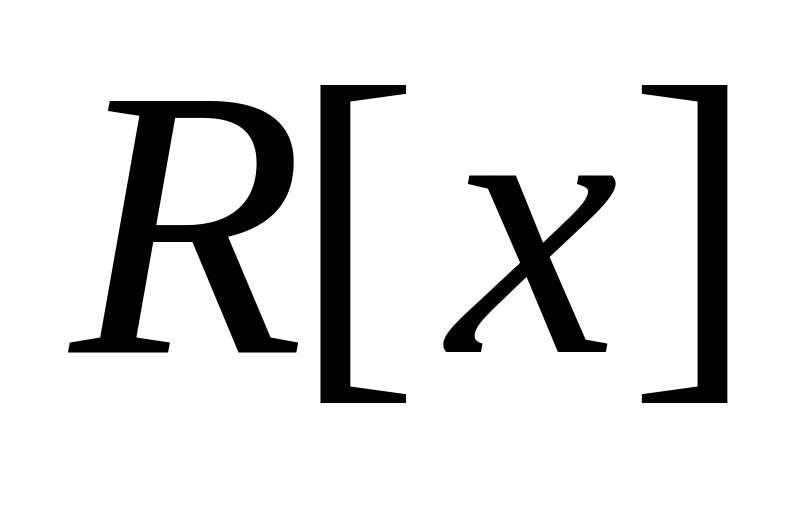2. Множество классов вычетов – кольцо классов вычетов Z_n.

Поскольку операции над классами вычетов сводятся к операциям над числами из этих классов, то свойства ассоциативности и коммутативности этих операций вытекают из аналогичных свойств числового сложения и умножения. То же замечание относится и к свойству дистрибутивности. Роль нулевого элемента при сложении играет класс . Противоположным элементом для класса вычетов является класс . Из определения сложения классов следует, что .

Кольцо называется коммутативным, если для любых .

В примерах 1-3 все кольца коммутативные.

Определение. Элемент кольца a  K называется обратимым, если существует элемент b  K , т.ч. a b = 1.

В кольце целых чисел Z обратимы лишь 1 и –1, всякое другое в кольце Z не имеет обратного, так как .

Утверждение. Множество обратимых элементов кольца образует мультипликативную группу.

Пример. Z_n^* – группа обратимых элементов кольца Z_n .

Поля

Коммутативное кольцо с единицей, в котором всякий ненулевой элемент обратим, называется полем.

Множество ненулевых элементов поля относительно умножения образует в силу определения поля коммутативную группу, которая называется мультипликативной группой поля.

Простейшими примерами числовых полей являются поле рациональных чисел и поле действительных чисел относительно операций сложения и умножения чисел. Можно доказать, что при любом простом (и только в этом случае) кольцо вычетов Z_p является полем. Оно называется полем вычетов по модулю .

Определение. Характеристикой поля называется наименьшее число m , т.ч. сумма m единиц поля равна 0. Если сумма единиц поля не равна 0 ни при каком m , то характеристика поля равна 0.

Поля и – поля характеристики 0. Поле Z_p имеет характеристику p.

Определение. Пусть задано поле ( E, +,  ) . Подмножество F  E c операциями поля E называется подполем поля E , оно является полем относительно этих операций. Поле E в этом случае называется расширением поля F .

Пример.Поле действительных чисел R является расширением поля рациональных чисел Q.