§ 5 Алгоритм последовательного возведения в квадрат

(http://granitnayki.com/?cat=6)

Пусть необходимо вычислить

y = a^x mod n,

где a – неотрицательное целое число, меньшее n ( a< n ), x  0.

Для вычисления y = a^x mod n применяем

Алгоритм последовательного возведения в квадрат

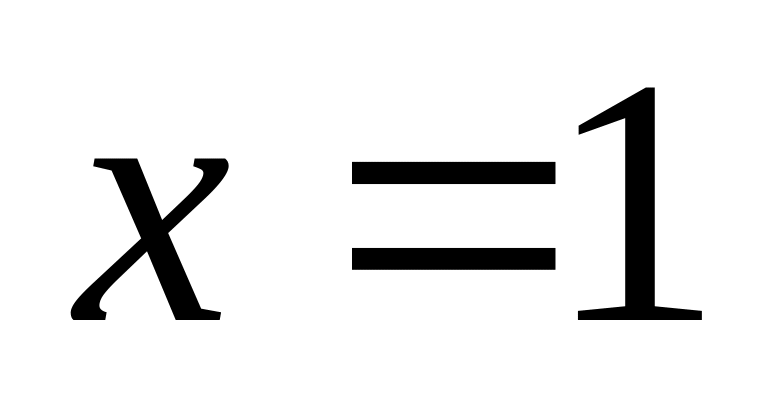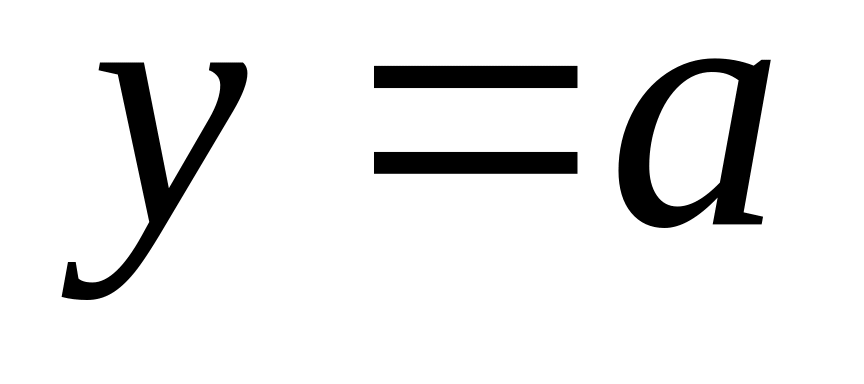
1. Если , то закончить работу алгоритма.

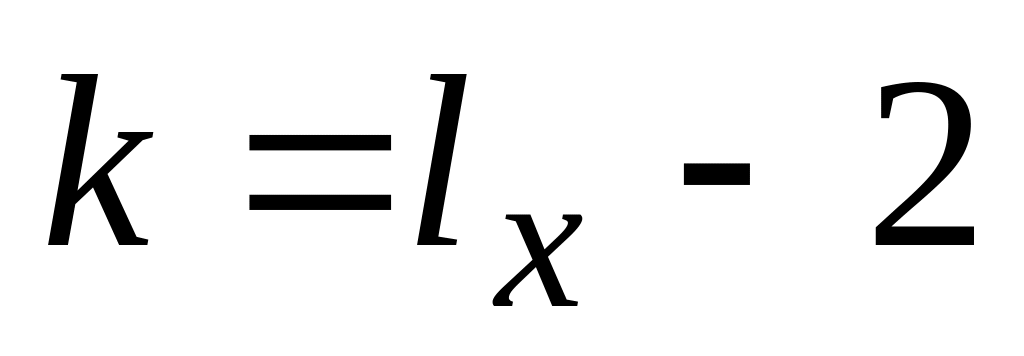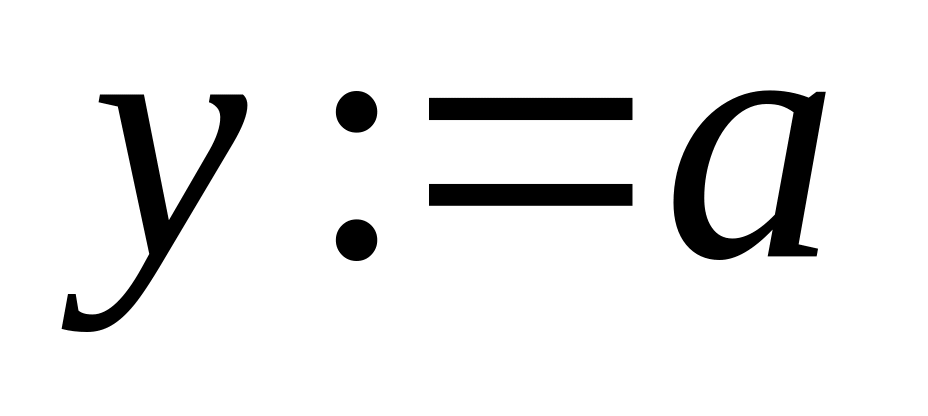2. , , где 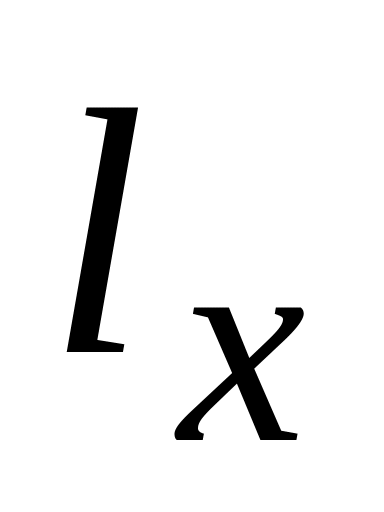- длина x в битах.

3. Для i от k до 0 выполнить шаги 4 и 5.

4. .

5. Если i-й бит x=1, то .

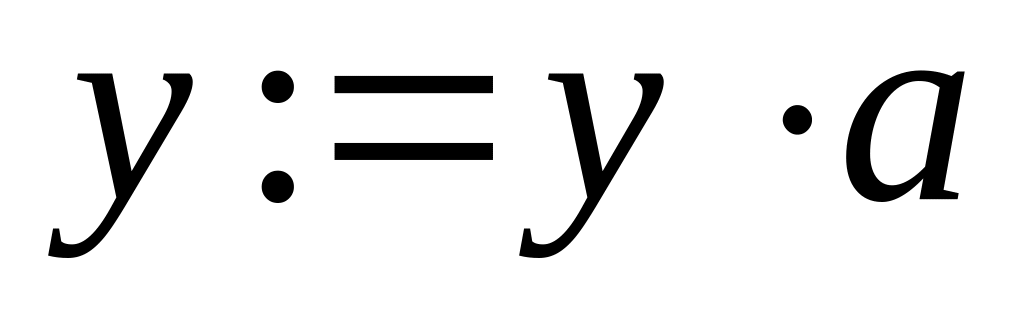6. Закончить работу алгоритма.

Этот алгоритм называется также SX-алгоритмом (http://granitnayki.com/?cat=6). Смысл такого названия состоит в следующем: считаем, что S(squaring) соответствует операции возведения в квадрат, а X – операции умножения на основание. К примеру, возведем основание a  в степень 23 по модулю  p. Запишем 23 в двоичной системе счисления как 10111. Далее, пропуская самый левый бит, который всегда равен 1 запишем под каждой цифрой 1 SX, а под каждой цифрой 0 – X.

1	0	1	1	1
	S	SX	SX	SX

Двигаясь слева направо, получим определяющую строку SSXSXSX. Помня, что S – это возведение в квадрат, а X – умножение на основание, получаем следующую последовательность операций:

(((((((((((a²mod n)²)mod n)*a) mod n)² mod n)*a) mod n)² modn)*a) mod n)=a²³ mod n,

что соответствует действительности.

Пример. Вычислить 2¹⁸ mod 13, параметры: a = 2, k = 18, n =13.

x = 2⁴ +2¹ ( 1, 0, 0, 1, 0 )

1. y:=2

2. k:=3

3(4-5). i = 3 x₃ = 0 y:=2² mod 13 = 4

i = 2 x₂ = 0 y:=4² mod 13 = 3

i = 1 x₁=1 y:=3² mod 13 = 9 y:=y*2 mod 13=5 y=5

i = 0 x₀=0 y:=5² mod 13 = 12

6. y = 12

Таким образом, 2¹⁸ mod 13 = 12.

Контрольные вопросы

1. Опишите алгоритм последовательного возведения в квадрат.

2. В каких криптографических алгоритмах необходимо вычислять степени числа по модулю?

§ 8 Дискретный логарифм

Задача дискретного логарифмирования: при заданных значениях параметров a, b и p, p – простое число, 1 < a, b < p, найти x , удовлетворяющий сравнению

b = a ^x mod p .

Определение. Дискретным логарифмом l числа b при основании a по модулю p называется степень, в которую нужно возвести число a, чтобы получить число b :

b = a ^l mod p .

Другое название дискретного логарифма l – индекс числа b при основании a по модулю p .

Принятые обозначения : log _a b и ind _a b .

Определение. Наименьшая степень, в которую нужно возвести число a по модулю p , чтобы получить 1 , называется порядком числа a . Обозначение - ord a .

Утверждение. Пусть p – простое число. Максимальный порядок числа по модулю p равен p – 1.

Утверждение. Пусть p – простое число, параметры a, b удовлетворяют неравенствам 1<a, b<p. Тогда сравнение b = a ^x mod p имеет единственное решение относительно x, если порядок числа a равен p – 1.