2.5 Приведение статических моментов, усилий, моментов инерции и движущихся масс к одному движению

2.5.1 Общие принципы решения задач приведения

Механическая часть электромеханической системы электропривода представляет собой сложную систему, включающую связанные движущиеся массы: двигателя, передаточного устройства и исполнительного механизма машины. Непосредственное представление о движущихся массах установки и механических связях между ними дает кинематическая схема электропривода. В кинематической схеме различные элементы системы движутся с разными скоростями, поэтому непосредственно сопоставлять их моменты инерции J_i, массы m_j, нельзя. Поэтому одной из первых задач проектирования и исследования электроприводов является составление упрощенных расчетных схем механической части.

Задача может быть решена просто, если реальная систе­ма двигатель – передача – рабочая машина заменяется некоторой эквивалент­ной системой, движущейся с одной скоростью (обычно это скорость двигателя ω) и которая описывается лишь одним уравнением движения.

Эквивалент­ная система с приведенными значениями параметров должна обладать теми же статическими и динамическими свойствами, что и реальная система. При инженерных расчетах механические связи можно принять абсолютно жесткими (не учитывать упругость звеньев и наличие зазоров в передачах). Тогда движение одного элемента дает полную информацию о движении всех остальных элементов, и достаточно рассматривать один элемент. В качестве такого элемента обычно принимают вал двигателя.

Таким образом, чтобы решить задачу приведения, надо составить урав­нения баланса кинетических энергий, мощностей для реальной и эквивалентной систем c учетом потерь мощности в системе.

Задача приведения показана на примерах (рис.2.7,а и 2.7,б) систем электропривода с вращательным и поступательным движе­ниями механизмов.

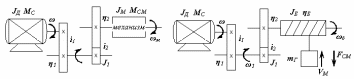
а) б)

Рис.2.7 Кинематические схемы механизмы с вращательным движением и поступательным движением механизмов

Принятые обозначения на рис.2.7:

J_Д, J₁, J_М, J_Б – моменты инерции двигателя и деталей на его валу, деталей на промежуточном валу, рабочей машины и барабана;

ω, ω₁, ω_Б – скорости вращения двигателя, промежуточного вала и рабочей машины;

i₁, i₂, η₁, η₂ - передаточные числа ступеней передач и их КПД;

η_Б – КПД рабочей машины;

M_C, M_CM – приведенный к валу двигателя момент сопротивления, момент сопротивления рабочей машины;

m_Г, V_М, F_СМ – масса груза, линейная скорость перемещения и сила сопротивления рабочей машины.

2.5.2 Приведения при вращательном движении механизма

Приведение М_С и М_СМ при двигательном режиме работы электропривода (рис.2.7,а). В этом случае поток энергии идет от двигателя к механизму (потери в передачах покрывают­ся за счет мощности, забираемой двигателем из электрической сети) и уравнение баланса мощности будет

Р_М = Р_Д ·η , (2.7)

или уравнение моментов

М_СМ · ω_М = М_С · ω · η , (2.8)

где η =η₁ · η₂ - общий КПД передаточного устройства.

В зависимости от постановки задачи по уравнению (2.7) баланса мощности определяются с учетом передаточного числа

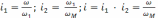(2.9)

момент сопротивления, приведенный к валу двигателя

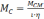
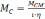; (2.10)

или статический момент, приведенный к валу рабочей машины

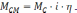(2.11)

Приведение М_С и М_СМ при тормозном режиме работы электропривода. В этом случае поток энергии направлен из рабочей машины через пе­редаточное устройство и двигатель в сеть при рекуперативном торможении либо в резисторы при других режимах торможения (потери в передачах покрываются за счет мощности, поступающей от рабочей машины).

Уравнение баланса мощности в этом случае

P_Д =P_M ·η , (2.12)

или уравнение моментов (2.13)

Момент сопротивления, приведенный к валу двигателя, определится, как 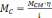, (2.14)

либо статический момент, приведенный к валу рабочей машины

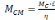. (2.15)

Приведение моментов инерции. Как было указано выше, для приведения моментов инерции необходимо составить уравнение баланса кинетической энергии в системе. При этом общий запас кинетической энергии эквивалентной системы может быть выражен через момент инерции, приведенный к валу двигателя J_ПР.Д, или через момент инерции, приведенный к валу вращающегося механизма J_ПР.М.

Уравнение баланса кинетической энергии:

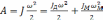. (2.16)

Таким образом, для кинематической схемы по рис. 2.7,а при приведении моментов инерции к валу двигателя:

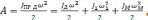(2.17)

откуда приведенный к валу двигателя момент инерции всей системы будет

(2.18)

При приведении к валу механизма уравнение баланса кинетической энергии запишется так:

(2.19)

откуда определяется момент инерции системы, приведенный к валу рабочей машины:

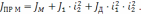
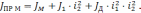(2.20)