3. Переходные процессы под нагрузкой.

   1. Пуск при реактивном моменте на валу

Если нагрузка представляет собой реактивный момент, переходный процесс пуска следует рассматривать на двух интервалах времени. На первом этапе электропривод заторможен реактивной нагрузкой и возрастание ω₀=ε₀t вызывает линейное возрастание момента короткого замыкания двигателя M_кз=ω₀β=β·ε₀·t. При M_кз=M_с начинается движение привода, и можно определить время запаздывания начала движения, как t_з=M_c/βε₀=∆ω_c/ε₀. С момента времени t=t_з изменение скорости описывается уравнением (7.25) и изменение момента уравнением (7.26), причем (ε₀t)_нач=∆ω_с ,ω_нач=0, М_нач=М_с.

Заданное значение скорости ε₀(t-t₃) отстоит от кривой ε₀=ε₀t по вертикали на отрезок ∆ω_с, что определяет суммарный перепад скорости ∆ω=∆ω_с+ε₀T_м. Момент двигателя на этом этапе нарастает от М=М_c до М_п.уст=М_с+ε₀J по экспоненте за время 3T_м. Зависимости ω, М(t) и механические характеристики приведены на рис.7.10.

Второй этап заканчивается в момент времени, когда управляющее воздействие достигает требуемого установившегося значения и его дальнейший рост прекращается. Двигатель при этом выходит на естественную механическую характеристику, и в дальнейшем имеет место процесс, описываемый уравнениями (7.4-7.5) при соответствующих начальных условиях. Как было выше установлено, скорость на этом участке нарастает по экспоненте, а момент уменьшается по тому же закону, стремясь к М_с .

Рис.7.10 Механические характеристики и переходные процессы

при пуске с реактивным моментом и w₀(t) = e₀t

3.2 Пуск при активном моменте

Как показано на рис. 7.11, при активном моменте сопротивления w_с(t) располагается ниже w₀(t) на Dw_c и никаких существенных отличий в алгоритме решения задачи нет по сравнению с пуском при M_c=0. Возможны два случая пуска - первый, когда при t = 0 w = -∆ω_с, т.е. когда до начала пуска привод вращался под действием активного М_с с небольшой скоростью и второй, когда растормаживание привода с активным моментом и начало роста w₀(t) совпадают. Для обоих случаев имеем w₀(t)=ε₀·t и ω_с(t)=a+kt = -∆ω_с+ ε₀·t.

Рассмотрим режим пуска по первому варианту, когда ω_нач=-∆ω_с .

Подставив параметры ω_с и начальную скорость в уравнение (7.23), получим:

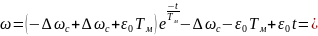
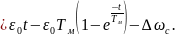(7.31)

Ускорение привода

В соответствии с полученными уравнениями скорость, начиная с начального значения ω_нач=--∆ω_с возрастает, асимптотически приближаясь к линейной зависимости с ускорением ε₀.

Изменение момента определим из уравнения (7.24) подставив в него параметры w₀(t), ω_с(t) и значение начальной скорости привода :

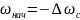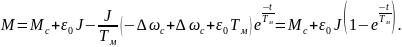(7.32)

Момент, как и ускорение привода, изменяясь по экспоненциальному закону, принимают установившиеся значения при t ≈3T_м , равные ε=ε₀ и M_{п max}= ε₀J.

Рис.7.11 Механические характеристики

и переходный процесс пуска при активном М_с

На втором этапе пуска скорости и момент привода изменяются, как и во всех предыдущих примерах, по экспоненте от установившихся значений в конце первого этапа.