7.4 Переходные процессы при линейном изменении управляющего воздействия

При пуске электропривода включением его в сеть на полное напряжение переходные процессы протекают при скачке напряжения, или как говорят, при ω₀=const. Применение реостатных методов ограничения бросков тока и момента не может обеспечить переходные процессы с максимальным быстродействием. Переходные процессы, близкие к оптимальным, можно получить путем плавного изменения управляющего воздействия. Они протекают в этом случае при ω₀=f(t). При этом ограничивается темп нарастания управляющего воздействия путем ограничения ускорения ε₀.

Уравнение линейной механической характеристики двигателя с отрицательной жесткостью может быть записано:

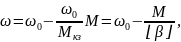(7.17)

где M_кз – момент короткого замыкания двигателя,

β=с²/R_я – жесткость механической характеристики.

Подставив (7.17) в основное уравнение движения привода после простых преобразований будем иметь:

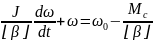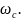= (7.18)

Коэффициент при производной угловой скорости представляет собой известную электромеханическую постоянную времени Т_м. Правая часть уравнения представляет собою скорость w_с, соответствующую моменту сопротивления М_с, однако, в рассматриваемом случае w₀, а значит и w_с не постоянные величины, а известные функции времени w₀(t) и w_c(t). Таким образом, уравнение (7.18) имеет вид:

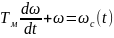. (7.19)

Определим решение этого дифференциального уравнения w(t) при линейном изменении w_с во времени. Для получения зависимости момента двигателя М(t) нужно в уравнение движения подставить производную функции w(t):

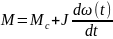. (7.20)

Для начала исследования принимаем общее уравнение закона изменения задающего воздействия w_с(t) = а + kt. (7.21)

Тогда уравнение (7.19) с учетом (7.21) примет вид:

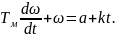(7.22)

Решение (7.22) определим в виде суммы свободной w_св и принужденной w_пр составляющих w = w_св + w_пр =A· .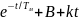

времени. Подставив w_пр и dω_пр/dt=k в (7.22) получим kT_м+ B + kt = a + kt, или B = a – kT_м .

Определим A с учетом начальных условий из полученного решения уравнения (7.22) w =A·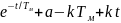 при t = 0 w = w_нач:

w_нач = А + а - kT_м, или А = w_нач - а + kT_м.

Таким образом, решение уравнения (7.22) будет иметь вид:

(7.23)

Определим решение уравнения (7.20) с учетом полученного выражения (7.23), определив производную скорости: .

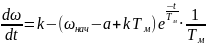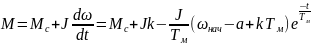. (7.24)

Рассмотрим переходные процессы в различных режимах работы электропривода.

1. Пуск привода вхолостую (М_с=0).

Так как пуск осуществляется при М_с = 0, в соответствии с механической характеристикой привода w_с(t) будет совпадать с w₀(t)=ε₀·t,

где ε₀ - ускорение, характеризующее темп изменения w₀.

Поскольку переходный процесс состоит из двух этапов, его необходимо рассчитать отдельно для каждого участка: при 0 < t < t₁, w_с(t) = e₀· t и при t > t₁, когда w_с(t) =w₀ = сonst.

I этап (0 < t < t₁).

Приняв, что при t = 0 w_нач = 0 и подставив в (7.23) а = 0 и k = e₀, получим

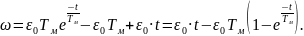(7.25)

Из уравнения (7.24) при М_с=0 и w_нач = 0 найдем закон изменения момента: 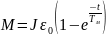(7.26)

Тогда ускорение привода будет 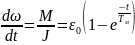, (7.27)

и скорость, изменяясь асимптотически, приближается к линейной зависимости.

При t > 3Т_м , считая изменение ускорения завершимся, т.е. dω/dt ≈ε₀, скорость изменяется в том же темпе, что и задающее воздействие, вызвавшее переходный процесс. Уравнение (7.25) при t > 3Т_м можно записать в виде:

w = e₀(t - Т_м) = w_с(t) - e₀Т_{м .} (7.28)

Поэтому кривая переходного процесса w(t) сдвинута вправо относительно кривой w_с(t) на величину Т_м, и в каждый момент времени при t > 3Т_м разница между w_с и w составляет e₀Т_м.

Механические характеристики при пуске и графики, описываемые уравнениями (7.25 – 7.28), представлены на рис.7.7.

Момент в соответствии с (7.26) возрастает по экспоненциальному закону и при t > 3Т_м достигает максимальной величины M_max=ε₀J. Это значение позволяет оценить допустимую величину ускорения. Действительно, если считать, что в переходном процессе М_max = М_доп, то ε_доп= М_доп/J.

По допустимым значениям ускорения и момента можно найти минимальное время на 1 этапе пуска привода:

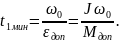
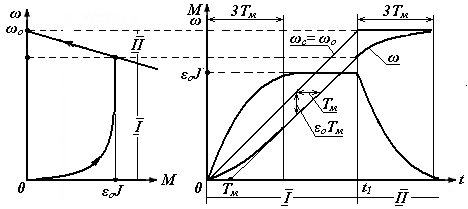
Рис.7.7 Механические характеристики и переходные процессы

при пуске ДПТ НВ вхолостую с ω₀(t)=ε₀t

II этап (t > t₁).

На II этапе режим определяется естественной механической характеристикой при постоянном задающем воздействии и w_с =w₀. Переходный процесс в этом случае ничем не отличается от рассмотренных ранее переходных процессов в разделе 7.2. При отсчете времени от t₁ скорость w и момент М будут изменяться в соответствии с уравнением (7.4), где начальными значениями будут ω_нач=ω(t₁) и M_нач=ε₀J, конечными – ω₀ и 0.

Графики переходных процессов w(t) и M(t) на II этапе показаны на рис.7.7, там же приведена динамическая механическая характеристика для случая пуска вхолостую.

2. Реверс при M_c=0.

При реверсе двигателя скорость w₀ меняет направление, причем изменение w₀ осуществляется по линейному закону при 0< t < t₁, затем при t > t₁ w₀ =const.

Переходный процесс в этом случае состоит из двух участков, которые рассматриваются отдельно. Так как переходный процесс осуществляется вхолостую (М_с = 0), то w_с(t) = w₀(t).

I этап (0 < t < t₁).

На I этапе w_с(t) описывается уравнением (7.21), и подставив его в уравнение (7.23) а = w₀, k = -e₀ и w_нач = w₀, получим:

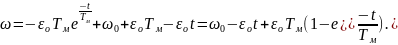(7.29)

Изменения момента М описываются уравнением:

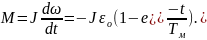(7.30)

Ускорение привода из (7.30) описывается 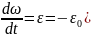), начальное значение которого равно нулю. При t > 3Т_м ускорение принимает установившееся значение ε≈ε₀ и скорость двигателя уменьшается по линейной зависимости w = w₀₁ - e(t - Т_м) = w_с(t) + eТ_м . Как и при пуске, кривая w(t) располагается правее кривой w_с(t) , причем сдвиг по оси t составляет величину Т_м, а в каждый момент времени при t > 3Т_м разница между w_с и w составляет ε₀T_м. Момент отрицателен и изменяется по экспоненциальному закону до величины M_макс = - ε₀J .

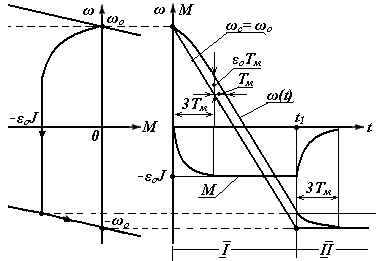
Рис.7.8 Механические характеристики и переходные процессы

при реверсе ДПТ НВ вхолостую с ω₀(t)=ε₀t

II этап (t > t₁).

Переходные процессы на II этапе описываются уравнениями экспонент, т.к. ω₀=const, причем скорость принимает установившееся значение, равное синхронной скорости, а момент – нулевое значение. Механические характеристики и кривые переходных процессов w_с(t), w(t) и М(t) показаны на рис.7.8.

При торможении вхолостую заданное значение скорости также изменяется по линейному закону от значения w₀ до нуля. Как и при реверсе, процесс состоит из двух этапов, причем на I этапе (0 < t < t₁ ) кривые w(t) и М(t) не отличаются от аналогичных кривых при реверсе, а на II этапе - описываются уравнениями (7.4-7.5) с начальными значениями ω_нач=ω(t₁), M_нач=-ε₀J, нулевыми конечными значениями и соответствуют режиму динамического торможения ДПТ НВ (рис.7.9).

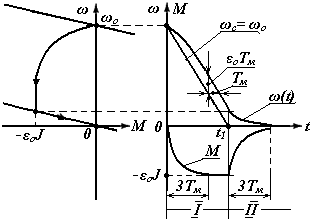
Рис.7.9 Механические характеристики и графики переходного

процесса при торможении вхолостую с w₀(t) = -e₀t