7.2 1 Расчет времени реостатного пуска дпт нв

В разделе 4.2.3 рассмотрен реостатный пуск ДПТ введением добавочных сопротивлений в якорную цепь, для которого выполним расчет времени пуска.

Время движения электропривода при пуске определим из основного уравнения скорости в переходном режиме по (7.4). Для времени t= после начала пуска скорость примет значение 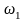угловой скорости. Тогда из уравнения (7.4) определим с учетом, что ω_у=ω_c1 , ω_нач1=0 и T_м=T_м1=J·(R_я+R_д1+R_д2)/c² :

Прологарифмировав полученное выражение, определим время работы привода на первой ступени пуска:

(7.6)

При работе на 2-й ступени пускового реостата параметры расчета будут:

T_м2=J·(R_я+R_д1)/c², ω_нач2=ω₁, ω_у=ω_с2.

И наконец, разгон по естественной электромеханической характеристике будет протекать при расчетных параметрах:

Т_м=J·R_я/c², ω_нач=ω₂, ω_у=ω_с.

По параметрам работы на искусственных характеристиках по уравнению (7.5) можно рассчитать время работы и значения токов при реостатном пуске ДПТ НВ. Полное время пуска определится как сумма значений времени работы двигателя на каждой характеристике.

Переходные процессы при реостатном двухступенчатом пуске ДПТ НВ приведены на рис.7.2.

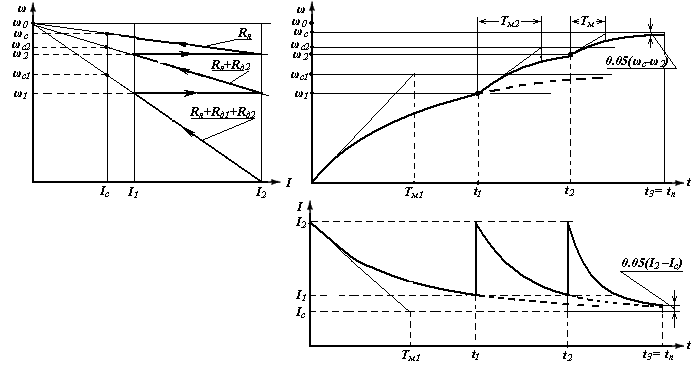
Рис 7.2 Пусковые характеристики ДПТ НВ при реостатном пуске

7.3 Переходные процессы в дпт нв c учетом электромагнитной инерции якоря

В электроприводах c питанием от сети электромеханические переходные процессы протекают практически при неизменном напряжении U, т.е. при ₀=const. Переходные процессы в этих условиях возникают при изменении управляющего воздействия _ скачком (пуск, торможение, реверс, останов) или изменении нагрузки (скачок нагрузки). Для ограничения тока при пуске или торможении до допустимых значений в цепь якоря двигателя вводится добавочное сопротивление. При этом электромагнитная постоянная якорной цепи Т_я=L_я/R_я значительно снижается, а электромеханическая постоянная Т_м, наоборот, увеличивается. Поэтому при работе двигателя на пусковых характеристиках влиянием электромагнитной инерции на протекание переходных процессов можно пренебречь, считая Т_я=0.

Необходимость учета Т_я обычно возникает при выходе двигателя для работы на естественной характеристике, когда добавочные сопротивления полностью выведены и влияние электромагнитной инерции может быть существенным.

С учетом принятых допущений в (7.2) переходные процессы в двигателе с независимым возбуждением с учетом индуктивности цепи якоря описываются системой уравнений:

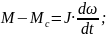
(7.7)

Решение приведенной системы уравнений относительно угловой скорости вращения при моменте сопротивления на валу, пропорциональном статической составляющей тока якоря (М_с=с·I_c), получим в виде:

,

или (7.8)

где T_я - электромагнитная постоянная времени якорной цепи,

ω_c – установившаяся угловая скорость при моменте сопротивления М_с.

Структурная схема электропривода, соответствующая системе уравнений (7.7), приведена на рис.7.3.

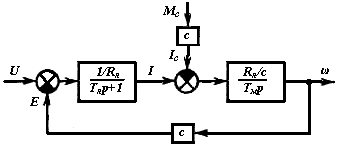
Рис.7.3 Структурная схема ДПТ НВ при L_я≠0

Характеристическое уравнение для (7.8) имеет вид:

. (7.9)

Корни характеристического уравнения:

. (7.10)

Соотношение постоянных времени является важным показателем динамических свойств электропривода, непосредственно определяющим колебательность разомкнутой электромеханической системы при жестких механических связях.

Если T_м>4T_я , корни характеристического уравнения p₁=-α₁; p₂=-α₂.

Электропривод может быть представлен в виде последовательного соединения двух инерционных звеньев с постоянными времени T₁ < Т₂ . Реакцию электропривода на скачок управляющего воздействия при нулевых начальных условиях и М_с=0 характеризуют переходная функция

(7.11)

и импульсная (весовая) функция

, (7.12)

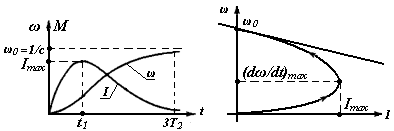
которые на рис.7.4,а отображают изменения угловой скорости и тока при пуске. Максимум тока I_max ≈ (dω/dt)_max возрастает при увеличении скачка управляющего сигнала (напряжения на якоре), поэтому скачок U должен быть ограничен значением, при котором I_mах остается в пределах, допустимых по перегрузочной способности двигателя.

а) б)

Рис.7.4 а) кривые переходного процесса ДПТ НВ при T_м>4T_я,

б) электромеханические характеристики

На рис.7.4,б приведены статическая и динамическая электромеханические характеристики ДПТ НВ, когда T_м>4T_я. Начальное значение тока якоря равно 0, а I_max<<I_кз.

При T_м< 4T_я характеристическое уравнение (7.9) имеет комплексно-сопряженные корни p_1,2= -α ± jβ и электропривод описывается колебательным звеном с коэффициентом затухания <1, и частотой собственных колебаний Ω_p. С учетом обозначений в передаточной функции колебательного звена, принятые в теории управления, можно записать:

(7.13)

где

Тогда корни характеристического уравнения будут .

Передаточная функция по току якоря из структурной схемы с учетом принятых обозначений будет 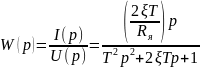(7.14)

Переходная функция колебательного звена (угловая скорость) при пуске двигателя вхолостую будет получена решением уравнения (7.13):

(7.15)

Решение уравнения двигателя относительно тока якоря получим из передаточной функции (7.14)

(7.16)

На рис.7.5 приведены переходные процессы, описываемые уравнениями (7.15) и (7.16).

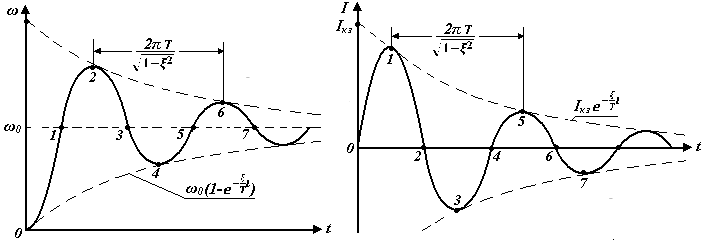
Рис.7.5 Переходные процессы ω(t) и I(t) при пуске ДПТ НВ c T_м< 4T_я

Таким образом, электропривод с линейной механической характеристикой вследствие электромагнитной инерции представляет собой при жестких механических связях колебательное звено, показатель колебательности которого  зависит только от соотношения постоянных времени (Т_м/Т_я), а быстродействие определяется электромагнитной постоянной времени Т_я или при данном отношении постоянных времени - эквивалентной постоянной времени Т.

Рис.7.6 Электромеханические (статическая и

динамическая) характеристики ДПТ НВ

Кривым переходных процессов скорости и тока якоря, представленных на рис.7.5, соответствует динамическая характеристика пуска ДПТ НВ вхолостую, приведенная на рис.7.6.