7. Процедуры и функции

7-1. Написать программу, которая выводит 12 значений N! с помощью функции:

1. не рекурсивной;

2. рекурсивной.

7-2. Написать процедуры, обрабатывающие числовые массивы и программы, демонстрирующие их применение:

1. заполнение массива случайными числами из указанного диапазона;

2. вывод массива на экран;

3. обмен значениями двух элементов массива;

4. поиск максимального (минимального) элемента массива;

5. поиск значения в массиве, с обработкой случая его отсутствия.

8. Некоторые стандартные алгоритмы

8-1. Напечатать все простые числа в промежутке от А до В с помощью «решета Эратосфена».

Простые числа от 2 до N определяются с помощью «решета Эратосфена» следующим образом:

берётся упорядоченный список всех чисел, которые изначально не выделены

выделяется самое маленькое из ранее невыделенных чисел

все числа, которые на него делятся, вычеркиваются из списка.

повторяем действия, пока не останется невыделенных чисел.

Оставшиеся (выделенные числа) и будут простыми числами.

8-2. Выполнить сортировку массива, используя ранее написанные процедуры из раздела "Процедуры и функции":

1. методом выбора;

2. методом вставок;

3. методом пузырька.

8-3. Применить бинарный поиск к заранее отсортированному массиву.

8-4. Выполнить одну из сложных сортировок:

1. пирамидальную сортировку;

2. быструю сортировку(Quick Sort).

9. Работа с графикой

9-1. Флаги различных государств являются примером достаточно простых (как правило) рисунков. Нарисовать флаги следующих  государств:

	Российский
	Французский
	Датский
	Исландский
	Греческий
	Британский
	Чешский
	Кубинский
	Японский
	Турецкий

 

9

50 квадратов

-2. ( 50 квадратов ) Написать программу, которая рисует 50 квадратов, вложенных один в другой, по следующему алгоритму. Сначала рисуется квадрат АВСD, затем на стороне АВ выбирается точка А', такая, что АА' = 0.05 * АВ. Точно так же вычисляется положение точек B', C', D' на сторонах ВС, СD, DA соответственно. После этого точкам А', B', C', D' присваиваются обозночения А, В, С, D, и процесс повторяется.

9-3. Построить графики следующих функций:

• логарифма y = ln(x);

• синуса y = sin(x);

• тангенса y = tg(x).

9-4. Построить параметрические кривые, зависящие от параметра t:

Улитка Паскаля:

x(t) = a cos²(t) + b cos(t),

y(t) = a cos(t) sin(t) + b sin(t);

a > 0, b > 0, tÎ[0, 2p]

Рассмотреть случаи, когда b ³ 2a, a < b < 2a, a > b.

Эпициклоида.

x(t) = (a + b) cos(t) - a cos((a + b) t/a),

y(t) = (a + b) sin(t) - a sin((a + b) t/a),

a > 0, b > 0.

Рассмотреть случаи, когда b/a = 3 и b/a = 3/2.

Строфоида:

х(t) = a(t-1) / (t+1), y(t) = at(t-1) / (t+1), a > 0

x(t) = a(t² – 1) / (t² +1), y(t) = at(t² – 1) / (t² + 1), a > 0

Построение каждой из кривых должно быть оформлено, как отдельная процедура или функция.

 

Фрактальная "снежинка"

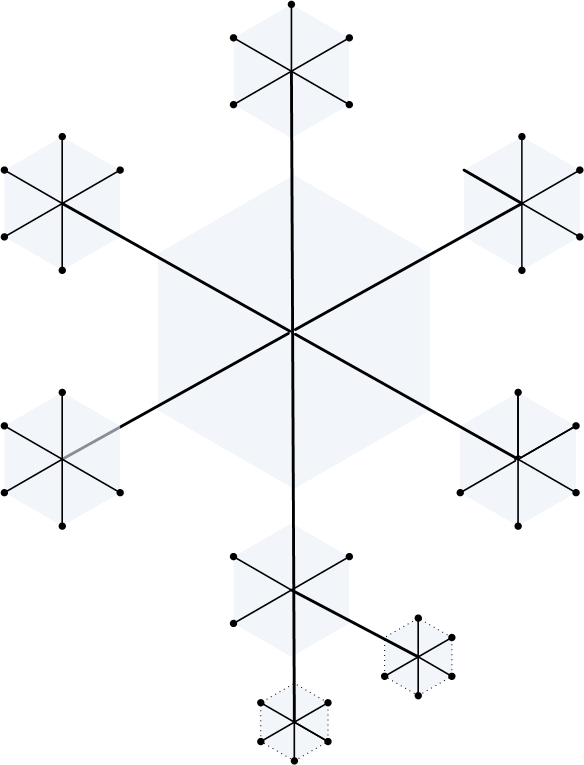
9-5. Предположим, что снежинка образуется так: из центра вырастает 6 кристалликов - отрезков длины L, углы между соседними отрезками равны 60; из их "свободных" концов ."вырастает" по 5 отрезков; соседние отрезки образуют углы по 60, длины этих отрезков в K раз меньше L; из их "свободных" концов аналогично вырастает по 5 новых отрезков, длина которых еще в К раз меньше, и так растет N "уровней" снежинки. Длина кристаллика на каждом уровне в K раз меньше длины кристаллика на предыдущем уровне. Написать программу, рисующую снежинку для любых заданных L, K, N.

 

 9-6. ( Треугольник Серпинского ) Узор (треугольник) Серпинского является одним из наиболее известных примеров фракталов, т.е. "самопдобных" фигур. Он рисуется следующим образом

• Б

  Треугольник Серпинского

  ерётся треугольник, как правило – равносторонний или равнобедренный.

• Определяются середины сторон.

• Соединяем полученые точки отрезками, получая треугольник в центре существующего.

• Удаляем центральный треугольник, получая фигуру, состоящую из трёх треугольников, соединённых углами.

• Повторяем процедуру для каждого из новых треугольников указанное число раз

.В качестве идеального математического объекта, треугольник Серпинского получается как предельная фигура после выполнения бесконечно большого числа иттераций.

Задача состоит в следующем.

1. выполнить указанное заранее количество итераций построения треугольника Серпинского и нарисовать результат;

2. показать процесс построения треугольника Серпинского при заданном заранее количестве итераций;

3. показать процесс построения, прерываемый нажатием клавиши.

9-7. На окружности берётся заранее указанное количество точек M.Каждая из них соединяется с точкой, отделённой от неё другими соседними точками. Число пропущенных точек N может быть произвольным. Построить рисунок при заданных M и N. (Идея данной задачи взята из журнала Hard&Soft.)