2. Задачи на условный экстремум, неопределенные множители Лагранжа

Метод множителей Лагранжа обычно применяется при решении задач отыскания экстремума соответствующего критерия опти-мальности, когда на независимые переменные наложены ограниче-ния в виде равенств. Пусть требуется найти экстремум функции

f (x1 , x2 ,...xn ) ,

(1.3.1)

зависящей от n переменных (i=1,2,..., n). Значения переменных x_i в свою очередь связанны соотношениями

φ_k (x₁ , x₂ ,...x_n ) = 0, k =1,2,..., m . (1.3.2)

Экстремум, который достигается функцией (1.3.1) с учетом вы-полнения соотношений (1.3.2), называется условным или связан-ным.

Число m соотношений (1.3.2) в изложенной постановке задачи должно быть меньше числа независимых переменных n. Если до-пустить равенство m = n , то в этом случае можно попытаться ре-

9

шить систему уравнений (1.3.2), поскольку число уравнений равно числу неизвестных. Полученное решение, если оно существует, определит дискретное множество точек (если эта система не имеет решения, то ограничения (1.3.2) определяют пустое множество). Поэтому решение задачи сведется к перебору допустимых точек (решений), удовлетворяющих соотношениям (1.3.2).

Если m < n , то в общем случае для решения задачи с такими ог-раничениями используется метод неопределенных множителей Ла-гранжа, сводящий задачу с ограничениями вида равенств к обыч-ной экстремальной задаче без ограничений. Это делается следую-щим способом:

• составляется вспомогательная функция n + m равно-

правных переменных x_i , λ_j ,(i = 1,2,..., n , j =,2,..., m)

Ф( x₁ , x₂ ,..., x_n , λ₁ , λ₂ ,..., λ_m ) = f ( x₁ , x₂ ,... x_n ) + λ₁φ₁ ( x₁ , x₂ ,... x_n ) +... + +λ _m φ_m ( x₁ , x₂ ,... x_n ),

(здесь λ₁ ,..., λ_k – дополнительные переменные, называе-мые неопределенными множителями Лагранжа);

• находится точка M с координатами x₁ , ... x_n , λ₁ , ..., λ_k (или точки, если их много) безусловного экстремума функции Ф;

• по найденной точке M определяется точка M , имею-щая координаты x₁ , ...x_n (найденные значения λ₁ , ..., λ_k

введенных переменных далее не рассматриваются); точ-ка M является точкой условного экстремума функции f , если такой экстремум существует.

Решим Пример 1.1 из раздела 1.2, применяя метод неопределен-ных множителей Лагранжа.

Функция Ф в этом примере имеет вид Ф = 2(a + b ) + λ (ab − S₀ ) .

Приравнивая частные производные от функции Ф по аргументам a , b, λ нулю, получим систему уравнений

2 + λb = 0, 2 + λa = 0,

ab = S₀ .

10

Последняя система уравнений решается с помощью исключения

переменных: a = −

2

и b = −

2

. После чего получается одно урав-

λ

λ

4

нение

= S

. Окончательно решение системы можно записать в

λ2

0

виде λ = −

2

и a =

S0 , b =

S0 (значение λ не может быть по-

S0

л ожительным, так как это приведет к отрицательным длинам a , b ; в математической постановке задачи программирования для кор-ректности сразу следовало ввести ограничения: a > 0 , b > 0 . Зна-

чение величины λ нас не интересует.

Понятно, что рассмотренный пример можно решить значитель-но проще. Учитывая ограничение ab − S ₀ = 0 , исключим одну из

переменных b = ^S_a⁰ . Тогда решение задачи сведется к оптимизации функции одного аргумента P = 2( a + ^S_a⁰ ) . Приравнивая нулю про-

изводную ^dP_da , получим оптимальное решение a = S₀ . Поэтому,

казалось бы, можно предложить следующий алгоритм решения за-дачи на условный экстремум:

• из системы уравнений (1.3.2) можно выразить m перемен-ных x_i 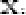как функции остальных m − n переменных, пред-ставить ограничения (1.3.2) в виде

x_k = ψ_k (x_{m +1},..., x_n ) , k =1,2,..., m ;

• подставить только что полученные соотношения в выраже-ние (1.3.1) и получить новую функцию, которая будет зави-сеть уже только от n − m переменных, не связанных допол-нительными условиями;

• найти безусловный экстремум новой функции.

Однако часто бывает трудно или вообще невозможно аналити-чески решить систему уравнений (1.3.2) относительно некоторых

11

переменных. Поэтому для отыскания экстремума функции многих переменных (1.3.1) с ограничениями (1.3.2) на независимые пере-менные в виде равенств используют метод неопределенных мно-жителей Лагранжа.

Метод неопределенных множителей Лагранжа получается из следующих рассуждений.

Общим необходимым условием экстремума является равенство нулю дифференциала функции

df =	∂f	dx	+ ... +	∂f	dx	= 0 .	(1.3.3)
	1				n
	∂x1			∂xn

Не имеет значения, наложены ли ограничения на дифференциа-лы аргументов.

Однако если ограничения наложены, то неправильно было бы приравнивать все частные производные нулю, поскольку диффе-ренциалы переменных dx_i (i =1,2,..., n) в выражении (1.3.3) не все

являются независимыми.

Предположим, что в некоторой точке x₀ с координатами x₁₀ , x₂₀ ,..., x_n0 функция f имеет экстремум. При этом условия

(1.3.2) в данной точке выполняются.

Продифференцировав условия (1.3.2), получим систему ра-венств, связывающих дифференциалы dx_i в любой точке, в том

числе и в точке x₀ :

n		∂φk
∑			dxi = 0, k =1,2,..., m .		(1.3.4)
=		∂x
i 1		i		( n − m) свободных дифферен-
Понятно, что можно выделить
циалов, например	dxm +1 ,..., dxn ,			а остальные	дифференциалы

dx₁ ,..., dx_m в каждой точке являются линейными функциями сво-

бодных дифференциалов.

Умножим каждое из равенств системы (1.3.4) на пока неопреде-ленный персональный множитель λ_k и сложим все эти равенства с

выражением (1.3.3).

Тогда, объединяя слагаемые с одинаковыми дифференциалами dx_i , найдем

12

n	∂f		∂φ		∂φ
∑(		+ λ1	1	+ ... + λ m		m ) dxi	= 0 .	(1.3.5)
	∂x
=			∂x		∂x
i 1	i		i			i

Равенство (1.3.5) должно быть справедливо в точке условного экстремума.

В соотношении (1.3.5) произвольно можно изменять лишь неза-висимые дифференциалы. Для того чтобы исключить m зависимых дифференциалов выберем m множителей λ₁ ,..., λ_k так, чтобы коэф-

фициенты при этих дифференциалах обратились в нуль в точке ус-ловного экстремума, т.е. обеспечим равенства

	∂f	+ λ	∂φ1	+ ... + λ	∂φm	= 0, i =1,2,..., m .	(1.3.6)
	∂x
		1	∂x		m ∂x
	i		i		i
Тогда в соотношениях (1.3.5) останется только ( n – m)							слагае-

мых с независимыми дифференциалами. Поскольку получена ли-нейная форма из независимых дифференциалов, равная нулю при любых их значениях, то коэффициенты этой формы должны быть равными нулю. Это означает, должны выполняться равенства (1.3.6) для остальных значений индекса i :

∂f	+ λ	∂φ1	+ ... + λ	∂φm	= 0, i = m +1,..., n .	(1.3.7)
∂x
	1	∂x		m ∂x
i		i		i

Понятно также, что координаты точки, где достигается услов-ный экстремум, удовлетворяют ограничениям (1.3.2). Таким обра-зом, совокупность уравнений (1.3.2), (1.3.6), (1.3.7) позволяет найти ( n + m) значений переменных x₁ , x₂ ,..., x_n , λ₁ , λ₂ ,..., λ_m , при которых

достигается условный экстремум функции (1.3.1), причем значе-ния неопределенных множителей нас уже не интересуют.

Легко проверить, что совокупность уравнений (1.3.2), (1.3.6), (1.3.7) может быть получена с помощью приравнивания нулю ча-стных производных от функции

Ф( x₁ , x₂ ,..., x_n , λ₁ , λ₂ ,..., λ_m ) = f ( x₁ , x₂ ,..., x_n ) +

+ λ₁φ₁ ( x₁ , x₂ ,..., x_n ) +... + λ _m φ_m ( x₁ , x₂ ,..., x_n ).

Значение метода множителей Лагранжа состоит и в том, что он применяется в качестве вспомогательного средства оптимизации в аналитических задачах. Например, он успешно используется при

13

решении задачи линейного статистического оценивания коэффици-ентов.