5.Примерные задания с решениями

Пример 1. Студент убеждён, что преподаватель намерен провалить его на экзамене, и пытается решить, стоит ли готовиться к очередному занятию. Если он подготовится, а преподаватель устроит на занятиях контрольную работу, студент может считать, что его итоговая оценка улучшится на 10 пунктов. Если контрольной не будет, знания, полученные при работе над заданием, позволяют рассчитывать на то, что оценка на экзамене улучшится на 5 пунктов. Вместо занятий студент может отправиться в кино и, если контрольной не будет, получить удовольствие на 3 пункта. Однако если контрольная состоится, а студент не занимался, его результат при этом будет 0.

a) Каким должно быть поведение студента?

b) Что будет делать преподаватель, если он и вправду намерен провалить студента на экзамене?

В этой задаче отношение между студентом и преподавателем рассматриваются как антагонистические, поэтому она может быть исследована с помощью матричных игр. Студент (игрок 1) имеет две стратегии:

1 — готовиться к занятию;

2 — не готовится к занятию.

У преподавателя (игрока 2) тоже две возможности:

1 — проводить контрольную работу;

2 — не проводить контрольную работу.

Выигрыш первого игрока (проигрыш второго) в каждой ситуации этой игры будем считать равным числу баллов, получаемых студентом. Найдём матрицу игры:

		Преподаватель
		1	2
Студент	1	10	5
	2	0	3

Легко видеть, что элемент этой матрицы — наименьший в первой строке и наибольший во втором столбце — является седловой точкой матрицы. Следовательно, студент всегда должен готовиться к занятиям, а преподавателю легче будет завалить студента на экзамене, если он никогда не будет устраивать контрольных работ.

Пример 2. Бомбардировочная операция. Два бомбардировщика (игрок 1) регулярно вылетают на задание. Один из них несёт бомбы, а другой — оборудование для создания помех радиолокационным станциям, оборудование для определения ущерба, нанесенного объекту и т. п. Бомбардировщики летят в таком строю, что первый из них находится под значительно большей эффективной защитой второго бомбардировщика, чем второй — под защитой первого. Имеются опасения, как бы носитель бомб не был сбит в результате атак истребителей противника (игрок 2). Проблема заключается в следующем: какой из бомбардировщиков должен быть носителем бомб, первый или второй, и какой из них должен быть атакован истребителями противника?

Здесь возможны следующие стратегии:

первый игрок:

1. носитель бомб в менее выгодном положении,

2. носитель бомб в более выгодном положении;

второй игрок:

1. атаковать бомбардировщик в менее выгодном положении,

2. атаковать бомбардировщик в более выгодном положении.

Предположим, что шансы носителя бомб уцелеть и выполнить задание равны 60 из 100, если он будет атакован в менее выгодном положении, 80 из 100, если он будет атакован в более выгодном положении, и 100, если он не будет атакован. Эта ситуация может быть представлена матрицей

Седловой точки у матрицы нет, поэтому оптимальные стратегии ищем среди смешанных стратегий. Используя формулы (25), (26), получим

; ;

.

Оптимальные стратегии: для первого игрока и — для второго. Цена игры — , то есть % бомб первого игрока достигнут цели вместо 80 % в случае если бы он ограничился применением только второй чистой стратегии, которая предпочтительнее первой.

Пример 5. Игра «блеф». Имеются две карты: старшая и младшая. Первый игрок выбирает одну из этих карт, смотрит на неё, не показывая второму. Посмотрев на карту, он может либо «пасовать», и тогда он должен заплатить второму игроку А рублей — на этом партия заканчивается, либо «вистовать». Если первый игрок «вистует», то второй может, не видя карт, либо «пасовать» — тогда второй платит первому А рублей и партия заканчивается, либо «вистовать». В последнем случае обе карты открываются и тот, у кого окажется старшая карта, получает В рублей от партнёра, В > А.

Эта игра начинается случайным выбором карты игроком 1. Будем предполагать, что с вероятностью 1/2 у него может оказаться любая из двух карт (карты не краплёные). Дальнейшее поведение первого игрока зависит от того, какую из возможных стратегий он выберет. Каждая стратегия должна представлять собой исчерпывающую инструкцию, предписывающую игроку поступать определённым образом в каждом из двух случаев. Таких стратегий у игрока 1 имеется четыре:

s₁ — если выбрана старшая карта, то «пасовать», если младшая, то «пасовать»;

s₂ — если выбрана старшая карта, то «пасовать», если младшая, то «вистовать»;

s₃ — если выбрана старшая карта, то «вистовать», если младшая, то «пасовать»;

s₄ — если выбрана старшая карта, то «вистовать», если младшая, то «вистовать».

У второго игрока всего две стратегии:

t₁ — «пасовать»;

t₂ — «вистовать».

Величину выигрыша первого игрока в каждой ситуации будем оценивать математическим ожиданием его выигрыша при появлении в игре этой ситуации.

При этом условии платёжная матрица игры «блеф» имеет вид:

	t1	t2
s1	–А	–А
s2	0
s3	0
s4	А	0

Поясним, как вычисляют элементы этой матрицы. Пусть, например, первый игрок применяют стратегию s₃ («вистует», когда ему достаётся старшая карта, и «пасует» в противном случае). Если второй игрок «пасует» (выбирает стратегию t₁), то первый игрок может выиграть А, если у него окажется старшая карта (он «вистует», партнёр «пасует»), и проиграть А, если у него младшая карта (он пасует и партия заканчивается). Так как то и другое происходит с вероятностью 1/2, то ожидаемый выигрыш 1-го игрока (проигрыш 2-го) равен

.

Следовательно, первый элемент третьей строки матрицы равен 0. Пусть теперь второй игрок «вистует» (стратегия t₂). Если у первого игрока старшая карта, то он «вистует» и выигрывает В, поскольку игроку достанется младшая карта. Если же у первого игрока младшая карта, то он «пасует» и должен заплатить партнёру А рублей. Средний его выигрыш в этой ситуации

это второй элемент третьей строки. Другие элементы матрицы вычисляются аналогично.

В полученной матрице игры первая и вторая строки доминируются третьей (и четвёртой) строкой. Поэтому первую и вторую стратегии можно исключить из рассмотрения и искать решения игры с матрицей:

	t1	t2
s3	0
s4	А	0

По формулам (25)–(26) найдём:

,

так что решение игры «блеф» имеет вид:

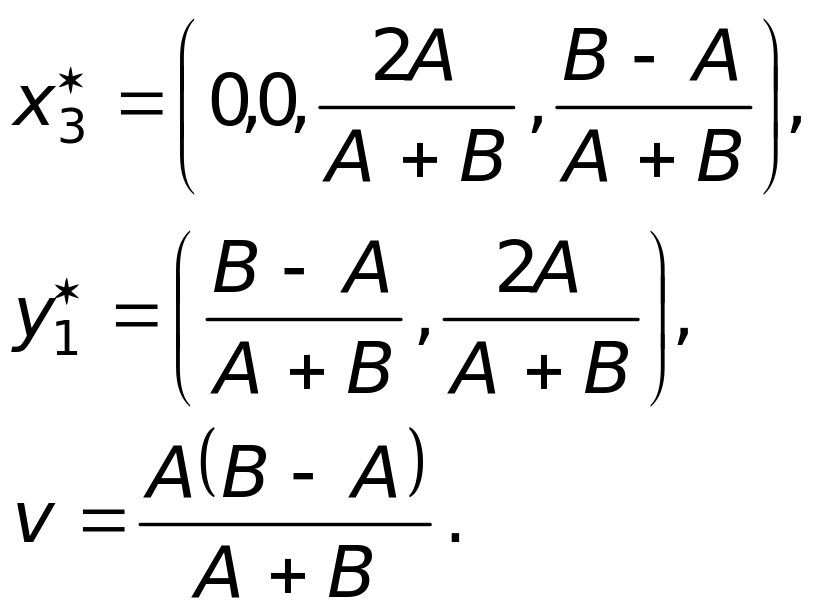
Стратегия s₄ игрока 1, предписывающая продолжение игры и в случае младшей карты, является «блефовой», так как она соответствует обычному пониманию блефа: игрок вистует без сильной карты на руках в надежде запугать противника и вынудить его к отказу от игры (к «пасу»). В полученном решении эта стратегия активна, то если для получения наилучшего результата в части играемых партий необходимо идти на блеф.

Пример 6. Рассматривается задача разработки оптимального плана энергетического строительства в некотором регионе. Предположим, что имеются возможности строительства электростанций четырёх типов: А₁, А₂, А₃ и А₄ (тепловые, гидравлические и т. д.). Эффективность каждого из четырёх типов объектов зависит от разнородных факторов (наводнения, засуха, морозы), а также от цены топлива, расходов на его транспортирование и т. п. Допустим, что можно выделить (по крайней мере, ориентировочно) пять различных случаев, каждый из которых обозначат определённое сочетание факторов, влияющих на возможную эффективность энергетических объектов. Назовём их состояниями природы и обозначим через В₁, В₂, В₃, В₄ и В₅.

Экономическая эффективность отдельных типов электростанций изменяется в зависимости от состояния природы в соответствии со следующей таблицей:

Таблица 1

		Состояние природы
		В1	В2	В3	В4	В5
Типы электростанций	А1	2	4	6	4	7
	А2	3	4	6	5	8
	А3	4	5	6	5	8
	А4	7	3	5	2	1

Будем рассматривать описанную ситуацию как игровую. Первый игрок (планирующие органы) располагает четырьмя стратегиями (по числу типов электростанций). Второй игрок («природа») действует случайно, но так, что к явлениям природы невозможно применить положение теории вероятностей. У него пять стратегий. В этих условиях табл. 1 является, по существу, игровой матрицей. Её анализ показывает, что у игрока 1 стратегии 1 и 2 доминируются стратегией 3 и поэтому могут быть исключены из рассмотрения. Приходим к игре матрицей:

	1	2	3	4	5
3	4	5	6	5	8
4	7	3	5	2	1

Теперь замечаем, что у игрока 2 стратегия 3 доминируется стратегией 2, а стратегия 2 — стратегией 4. Следовательно, имеет смысл анализировать игру 23, задаваемую матрицей:

	1	4	5
3	4	5	8
4	7	2	1

Пусть — произвольная смешанная стратегия игрока 1 в этой игре. Найдем функции :

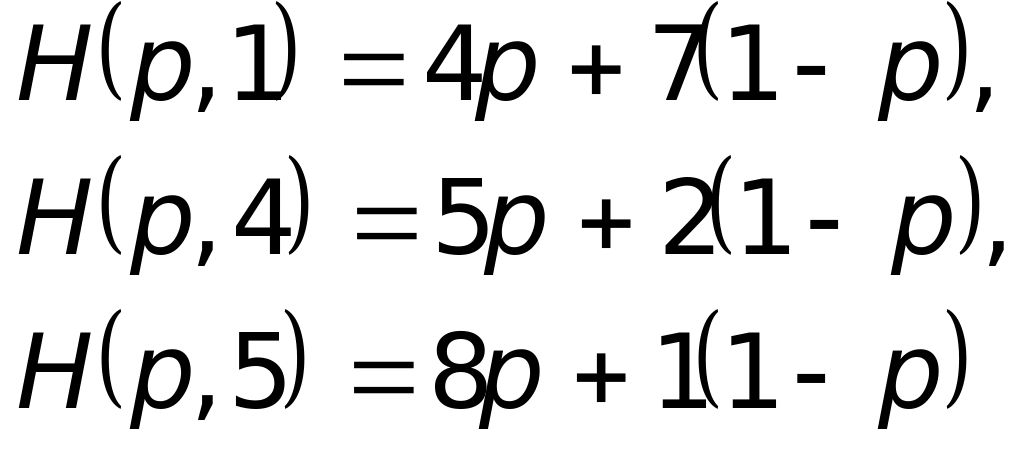
и построим их графики (рис. 6.3)

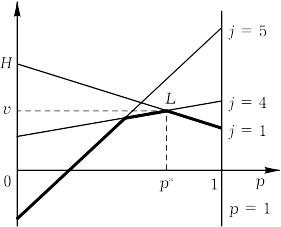
Рис. 6.3.

экстремальная точка L на нижней огибающей (отмечена жирной линией) является пересечением прямых, соответствующих 1-ой и 4-ой стратегиям игрока 2, поэтому рассматриваем игру 22:

	1	4
3	4	5
4	7	2

По формулам (25)(26) находим:

.

Из полученных результатов формируем решение исходной игры:

.

Таким образом, для обеспечения региона электроэнергией целесообразно ограничиться строительством электростанций типов А₃ и А₄ в пропорции 5:1. При этом экономическая эффективность такого решения никогда не будет ниже ; если же учесть, что второй игрок — природа — скорее всего не будет применять своей оптимальной стратегии, то можно рассчитывать на более высокий показатель эффективности.

Пример 7. Контроль качества. Радиотехническая фирма производит высококачественные усилители. Их работа существенно зависит от параметров небольшого дефицитного конденсатора. Производство этого конденсатора фирме обходится в 1 доллар, но она затрачивает 10 долларов при замене неисправного конденсатора у потребителя.

Для решения этой проблемы у фирмы имеется несколько возможностей: во-первых, фирме известен метод проверки конденсаторов, который гарантирует выявление неисправностей с вероятностью и его применение обходится в 1 доллар; во-вторых, существует очень дешёвый способ проверки (стоимость проверки одного конденсатора практически равна 0), всегда выявляющий неисправный конденсатор, но с вероятностью приводящий к пробою исправного конденсатора. Фирма может, наконец, закупать конденсаторы повышенного качества по 4 доллара с полной гарантией. Задача фирмы состоит в правильном выборе среди этих возможностей. Она сводится к решению следующей игры 42:

		Конденсатор
		Дефектный	Исправный
Фирма	1. Без проверки	–10	–1
	2. Проверенный за 1$	–17/4	–2
	3. Дешёвый способ проверки	–1	–10
	4. Покупать с гарантией	–4	–4

С помощью графического метода (см. рис. 6.4) мы находим, что активными стратегиями первого игрока является вторая и третья стратегии. Вероятность их применения найдем из игры 22:

		Конденсатор
		Дефектный	Исправный
Фирма	2.	–17/4	–2
	3.	–1	–10

, .

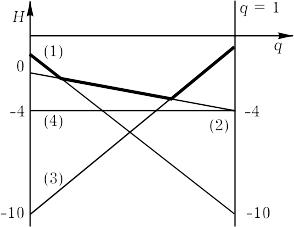
Рис. 6.4.

Поэтому оптимальная смешанная стратегия игрока 1 в первоначальной игре имеет вид:

.

Следовательно, фирма должна подвергать проверке все конденсаторы, причём всех произведенных конденсаторов проверяются по первому методу контроля, — по второму. Гарантированные конденсаторы по 4 доллара не закупаются.

Цена игры равна

.

Это — средняя стоимость одного конденсатора при самом неблагоприятном соотношении между дефектными и исправными конденсаторами, которое характеризуется оптимальной стратегией игрока 2:

.

Пример 8. Антагонистическая конкуренция. Фирма А производит некоторый сезонный товар, который имеет спрос в течении n единиц времени. Этот товар поступает на рынок в момент . Для конкурентной борьбы фирма В, не заботясь о собственных доходах, производит аналогичный товар, который поступает на рынок в момент . Её цель — разорение первой фирмы. Для этого проще всего продавать товар по пониженной цене. Однако иногда имеются законы или соглашения, запрещающие поступать подобным образом. В этом случае единственным законным инструментом фирмы В является выбор момента поступления товара на рынок.

Пусть качество конкурирующих товаров зависит от времени их поступления на рынок: чем позже товар выбрасывается на рынок, тем качество его выше, а реализуется только товар более высокого качества. Тогда, если фирма А выбросит свой товар в момент i, а фирма В — в момент j > i, то фирма А, не имея конкурента в течение j  i единиц времени, получит за это время доход c(j  i), где с — доход от продажи товара в единицу времени. В момент времени j на рынке появляется товар фирмы В, который имеет более высокое качество. Поэтому с момента j фирма А теряет рынок и в дальнейшем дохода не получает. Если же i > j, то фирма А, выбросив на рынок более качественный товар, будет получать доход в течении n  i + 1 оставшихся до конца рассматриваемого периода единиц времени, который будет равен c(n  i + 1). В том случае, когда i  j, то есть на рынок одновременно поступают оба товара, естественно считать, что эти товары имеют одинаковый спрос, и поэтому фирма А получит доход c(n  i + 1)/2.

Фирма А выбирает i-ю единицу времени поступления товара на рынок, стараясь максимизировать свой доход, а фирма В, выбирая j-ю единицу времени, преследует прямо противоположную цель — минимизировать доход фирмы А. Следовательно, рассматриваемая конкуренция двух фирм является антагонистическим конфликтом. Для построения математической модели — матричной игры — примем за игроков 1 и 2 соответственно фирмы А и В. У каждого из игроков имеется по n чистых стратегий в соответствии с n возможностями для выбора времени начала распродажи своего товара. Элементы платёжной матрицы определяют равенствами:

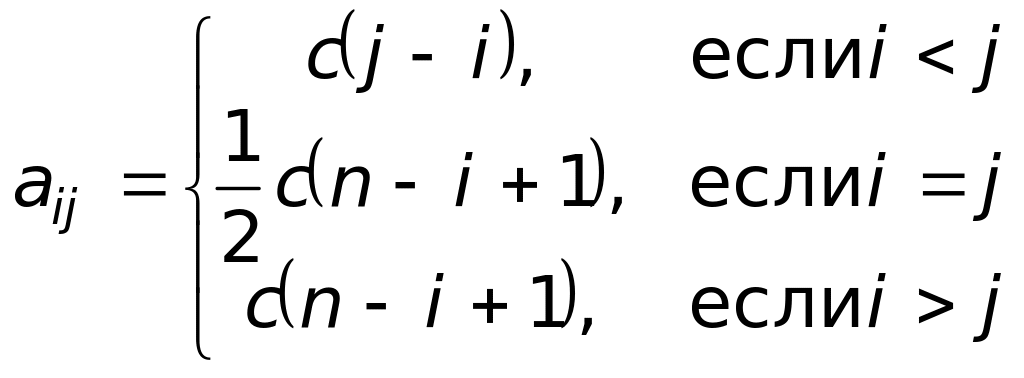(33)

Рассмотрим полученную игру при n = 5 и с = 1. Вычислив элементы платёжной матрицы по формулам (33), получим:

						Игрок 2 (фирма В)
			1		2		3		4		5		(34)
	Игрок 1 (фирма А)			1		2.5		1		2		3		4
				2		4		2		1		2		3 (34)
				3		3		3		1.5		1		2
				4		2		2		2		1		1
				5		1		1		1		1		0.5

Прежде чем использовать симплекс-метод, исключим из рассмотрении некоторые стратегии игроков, используя соображения доминирования. Так как пятая стратегия игрока 1 доминируется любой другой его стратегией, то игрок 1 без ущерба для себя может её опустить. После удаления пятой строки в полученной матрице первый столбец доминируется вторым, а пятый — четвёртым. Эти столбцы тоже могут быть удалены. Таким образом, мы приходим к игре с матрицей:

								Игрок 2 (фирма В)
		2		3	4	(35)
			Игрок 1 (фирма А)				1	1	2	3
							2	2	1	2
							3	3	1.5	1
							4	2	2	1

Все элементы этой матрицы положительны. Задача 1^* в рассматриваемом случае имеет вид:

найти вектор из условий:

2	+	3	+	4		max	(36)
2	+	23	+	34		1
22	+	3	+	24		1
32	+	3	+	4		1
22	+	23	+	4		1
2	,	3	,	4		0

После введения дополнительных переменных эта задача сводится к эквивалентной задаче:

2

+

3

+

4

+

05

+

06

+

07

+

08



max

2

+

23

+

34

+

5

+

+

+



1

22

+

3

+

24

+

+

6

+

+



1

32

+

3

+

4

+

+

+

7

+



1

22

+

23

+

4

+

+

+

+

8



1

2

,

3

,

4

,

5

,

6

,

7

,

8



0

Решение этой задачи симплекс-методом начнём с допустимого базисного решения

.

Ему соответствует симплексная таблица:

B	CB	XB	2	3	4	5	6	7	8
			1	1	1	0	0	0	0
5	0	1	1	2	3	1	0	0	0
6	0	1	2	1	2	0	1	0	0
7	0	1	3	3/2	1	0	0	1	0
8	0	1	2	2	1	0	0	0	1
		0	–1	–1	–1	0	0	0	0

Можно ввести в число базисных переменных переменную ₂. Так как , из базисных переменных удаляется переменная ₇. Элемент таблицы z₇₂ — разрешающий на данном шаге метода. Выделим его. Новая таблица будет такова:

B	CB	XB	2	3	4	5	6	7	8
			1	1	1	0	0	0	0
5	0	2/3	0	3/2	8/3	1	0	–1/3	0
6	0	1/3	0	0	4/3	0	1	–2/3	0
7	1	1/3	1	1/2	1/3	0	0	1/3	0
8	0	1/3	0	1	1/3	0	0	–2/3	1
		1/3	0	–1/2	–2/3	0	0	1/3	0

Теперь для ввода в число базисных переменных выберем ₄. Вычисляем и определяем, что из базисных переменных должна быть удалена переменная ₅. Элемент — разрешающий. Новая таблица имеет вид:

B	CB	XB	2	3	4	5	6	7	8
			1	1	1	0	0	0	0
4	1	1/13	0	9/16	1	3/8	0	–1/8	0
6	0	3/13	0	–3/4	0	–1/2	1	–1/2	0
2	1	2/13	1	5/16	0	–1/8	0	3/8	0
8	0	4/13	0	13/16	0	–1/8	0	–5/8	1
		7/13	0	–1/2	0	2/8	0	1/4	0

Выполнив ещё один шаг с разрешающим элементом , получим окончательную симплексную таблицу:

B	CB	XB	2	3	4	5	6	7	8
			1	1	1	0	0	0	0
4	1	1/13	0	0	1	6/13	0	4/13	–9/13
6	0	3/13	0	0	0	–8/13	1	–14/13	12/13
2	1	2/13	1	0	0	–1/13	0	8/13	–5/13
3	1	4/13	0	1	0	–1/13	0	–10/13	16/13
		7/13	0	0	0	3/13	0	2/13	2/13

Оптимальное решение задачи (34) — ; оптимальное решение двойственной к ней задачи — . Оптимальные значения целевых функций в этих задачах совпадают и равны . По формулам (32) находим решение игры с матрицей (35):

.

Решение исходной игры с матрицей (34) имеет вид:

цена игры ;

оптимальная стратегия игрока 1 (фирма А)

;

оптимальная стратегия игрока 2 (фирма В)

.

Таким образом, фирма А имеет значительные потери: в отсутствии конкурента её доход составил бы 5 единиц, теперь же она может рассчитывать на получение единиц дохода.

Пример 10. В соответствии со спросом на продукцию номенклатуры q в городе планируется построить предприятие по производству этой продукции. Неопределенность спроса в период t приводит к тому, что необходимо рассчитать объем выпускаемой продукции , который должен быть, по крайней мере, не меньше спроса на продукцию , чтобы не потерять потенциально возможный доход от реализации продукции, а также не должен превышать уровень спроса, так как предприятие будет нести убытки, связанные с уценкой. Предположим, что в течение года (по кварталам) спрос на продукцию номенклатуры q выражается величинами 20, 40, 60, 100 тыс. шт. Планирующий орган может принять одно из следующих решений: построить предприятие, которое выпускает соответственно 20, 40, 60, 100 тыс. шт. продукции в квартал. Предприятие терпит издержки от нереализованной продукции 10 руб./ед., доход от реализации составляет 40 руб./ед.

Платежную функцию примем в виде функции потерь

При изучении работы аналогичных предприятий планирующий орган может располагать или не располагать дополнительной информацией, снижающей неопределенность ситуации:

1. известны вероятности спроса на продукцию по кварталам года 0,2; 0,4; 0,3; 0,1;

2. спрос на продукцию в каждом квартале равновероятен;

3. о вероятностях спроса на указанную продукцию по кварталам сказать ничего нельзя.

Решение. В качестве статистика выступает планирующий орган, который может принять одно из четырех решений: стратегия A₁ — построить предприятие, выпускающее 20 тыс. ед., А₂ — 40 тыс. ед., А₃ — 60 тыс. ед., А₄ — 100 тыс. ед. продукции.

Природой будем считать совокупный спрос потребителей.

Аналогично, состояние П₁ — спрос, равный 20 тыс. ед., П₂ — 40 тыс. ед., П₃ — 60 тыс. ед., П₄ — 100 тыс. ед. продукции.

Описанная ситуация представляет собой статистическую игру. Найдем элементы платежной матрицы.

Стратегии статистика	Состояние спроса
	П1	П2	П3	П4
А1	800	800	800	800
А2	600	1600	1600	1600
А3	400	1400	2400	2400
А4	0	1000	2000	4000
Pj	0.2	0.4	0.3	0.1

Покажем, как были вычислены некоторые элементы.

В ситуации (А₁, П₁) плановый орган принял решение построить предприятие мощностью 20 тыс. ед., что соответствует coстоянию спроса в 20 тыс. ед. Доход от производства в 20 тыс. ед. продукции а₁₁ = 20•40 = 800 тыс. руб.

В ситуации (А₁, П₂) плановый орган принял решение построить предприятие мощностью 20 тыс. ед., спрос составляет 40 тыс. ед. Если бы предприятие обеспечило этот спрос, то доход от производства составил бы 40•40 = 1600 тыс. руб. Однако спрос удовлетворяется лишь на 20 тыс. ед., значит, предприятие недополучит доход 20•40 = 800 тыс. руб. Элемент а₁₁ = 40•40  (20•40) = 800 тыс. руб.

В ситуации (А₂, П₁) плановый орган принял решение построить предприятие мощностью 40 тыс. ед., спрос составляет 20 тыс. ед. Доход от реализации составляет 40•20 = 800 тыс. руб. Издержки хранения нереализованной продукции составляют 20•10 = 200 тыс. руб. Элемент а₂₁ = 40•20   (20•10) = 600 тыс. руб.

Аналогично рассчитываются и остальные элементы платежной матрицы.

Применим вышеописанные критерии к полученной игре.

Вычислим средние выигрыши :

= 800•0,2 + 800•0,4 + 800•0,3 + 800•0,1 = 800;

= 600•0,2 + 1600•0,4 + 1600•0,3 + 1600•0,1 = 1400;

= 400•0,2 + 1400•0,4 + 2400•0,3 + 2400•0,1 = 1600;

= 0•0,2 + 1000•0,4 + 2000•0,3 + 4000•0,1 = 1400.

Оптимальной стратегией по Байесу является А₃, так как ей соответствует наибольшая средняя прибыль а₃ = max (800, 1400, 1600, 1400) = 1600 (тыс. руб.).

По критерию Лапласа принимаем все q_i = 1/4, i = 1, ..., 4.

Тогда средние выигрыши равны

a₁ = 800•0,25 + 800•0,25 + 800•0,25 + 800•0,25 = 800;

а₂ = 600•0,25 + 1600•0,25 + 1600•0,25 + 1600•0,25 = 1350;

а₃ = 400•0,25 + 1400•0,25 + 2400•0,25 + 2400•0,25 = 1650;

а₄ = 0•0,25 + 1000•0,25 + 2000•0,25 + 4000•0,25 = 1750.

Оптимальной стратегией по Байесу является А₄, так как ей соответствует максимальная прибыль 1750 тыс. руб.

По критерию Вальда оптимальной является стратегия А₁, для которой гарантированная прибыль достигает наибольшей величины, равной 800. В самом деле,

а_i0 = a_i = a_ij = max(800, 600, 400, 0) = 800.

Построим матрицу рисков.

Стратегии статистика	Состояние спроса
	П1	П2	П3	П4
А1	0	800	1600	3200
А2	200	0	800	2400
А3	400	200	0	1600
А4	800	600	400	0

По критерию Сэвиджа оптимальной является стратегия А₄, для которой в наихудших условиях величина риска r принимает наименьшее значение, равное

r_i0, = r_i = r_ij = min (3200, 2400, 1600, 800) = 800.

По критерию Гурвица вычисляются значения выражений g_i =  a_ij + (1  ) a_ij для каждого i. Решение принимается по наибольшему из полученных результатов. Параметр  назначается лицом, принимающим решение. Подставляя данные матрицы платежей, имеем

g₁ = 800 + 800(1  ) = 800;

g₂ = 600 + 1600(1  ) = 1600  1000;

g₃ = 400 + 2400(1  ) = 2400  2000;

g₄ = 0 + 4000(1  ) = 4000  4000.

Ответ зависит от . При  < 0,8 принимается решение А₄. При  = 0,8 все критерии дают один результат. При  > 0,8 принимается решение А₁.

Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалось решение А₄. Следовательно, нужно строить предприятие мощностью 100 тыс. ед. Прибыль при этом, если вероятности спроса известны, составит 1400 тыс. руб., при равновероятных состоят спроса 1750 руб.

Пример. Рынок трех лиц.

Пусть продавец (Пр) обладает единицей неделимого товара, а два потенциальных покупателя (П₁ и П₂) хотят приобрести этот товар. Продавец оценивает свой товар в а денежных единиц, а покупатели в b и с денежных единиц соответственно. Это означает, что цена, по которой будет продан товар, для продавца должна быть не меньшей а, а для покупателей — не большей b и с соответственно. Для того чтобы все три лица могли участвовать в сделке, будем предполагать, что а < b < с.

Для игрового моделирования описанной ситуации рассмотрим кооперативную игру с множеством игроков I = {Пр, П₁, П₂} и характеристической функцией v(S), где S — множество игроков, участвующих в сделке, a v(S) — сумма полученных ими прибылей. Очевидно, нужно положить v(Пр) = v(П₁) = v(П₂) = 0, v(П₁, П₂) = 0, так как ни продавец без покупателя, ни покупатели без продавца никакой прибыли себе обеспечить не могут. Если сделка состоится между Пр и П₁, и товар будет продан по цене р, а  р  b, то Пр получит прибыль р  а, а П₁ — прибыль b  р. Поэтому

v(Пр, П₁) = p  a + b  p = b  a.

Аналогично v(Пр, П₂) = с  а. Для коалиции v(Пр, П₁, П₂) прибыль тоже равна с  а. Эта коалиция образуется, например, тогда, когда П₂, приобретая товар, платит часть своей прибыли П₁ за совместные действия, направленные на снижение цены.

Пример. Задача о бригаде рабочих.

Пусть бригада, состоящая из четырех рабочих, которых наделим номерами 1, 2, 3, 4 совместно выполнила некоторую работу. Кроме того, известно, что эту же работу могли бы выполнить первый с любым из остальных рабочих и все рабочие без первого. Определим функцию v(S), присваивая коалиции S выигрыш 1, если она в состоянии выполнить работу, и 0 в остальных случаях. Получим:

v(1) = v(2) = v(3) = v(4) = v(2, 3) = v(2, 4) = v(3, 4) = 0;

v(1, 2) = v(1, 2, 3) = v(1, 2, 4) = v(1, 2, 3, 4) = 1;

v(1, 3) = v(1, 3, 4) = 1;

v(1, 4) = 1;

v(2, 3, 4) = 1.

В этой задаче естественным образом возникает желание найти дележ x = (x₁, x₂, x₃, x₄), «справедливым» образом распределяющий между рабочими общую плату за работу.

Пример. Кооперирование предприятий

Пусть 3 предприятия производят два изделия, причем первое изделие изготовляется только на первом предприятии, второе на втором и третьем. Объемы выпуска изделий предприятиями приведены в таблице:

	Предприятия
Изделия	1	2	3
I	1000	–	–
II	–	900	700

Предполагается, что изделия покупаются только комплектами: одно изделие вида I и одно изделие вида II. Стоимость одного комплекта — 2 денежные единицы. Спрос на поставляемые комплекты предполагается неограниченным.

Понятно, что в данной ситуации предприятия могут обеспечить себе доход только на основе кооперирования. Рассмотрим кооперативную игру Г = I, v, где I = {1, 2, 3}. Для вычисления значений характеристической функции v(S) будем измерять выигрыш стоимостью комплекта, выпускаемых коалицией S.

Очевидно, для v(S) получим следующие значения:

v(1) = v(2) = v(3) = v(2, 3);

v(1, 2) = 1800; v(1, 3) = 1400; v(1, 2, 3) = 2000.

Максимальный доход, который могут обеспечить себе предприятия совместными действиями, равен 2000. Цель задачи — найти распределение этого дохода между предприятиями, учитывая всю имеющуюся у них информацию.

Пример. Пусть Покупатель 1 (П₁) решил потратить на аукционе 2500 руб., Покупатель 2 (П₂) — 2200 руб. На аукцион выставлены 2 предмета. По мнению Покупателя 1, первый предмет, выставленный на аукцион, стоит 1000 руб., второй — 2000 руб. Тогда Покупатель 1 будет повышать цену на первый предмет до величины

р = (2(1000  2000) + (2500 + 2200))/4 = 675 руб.

Допустим, что первый предмет куплен за эту цену, его купил П₂, то его доход равен Д₂ = 1000  675 = 325 руб., а доход П₁ равен Д₁ = 2000  1525 = 475 руб., разность доходов Д₁  Д₂ = 150 руб. В случае, когда первый предмет куплен П₁, то его доход равен Д₁ = 1000  675 = 325 руб., а доход П₂ равен Д₂ = 2000  1825 = 175 руб., разность доходов также равна Д₁  Д₂ = 150 руб.

Рассмотрим другую цель участника П₁ — получить максимум собственного дохода. Теперь он повышает цену и предлагает р + d за первый предмет, если это увеличит его собственный доход на аукционе. В этом случае его доход равен Д₁ = V₁  (р + d), что надо сравнить с Д₁ = V₂  (с  р + d), соответствующее его доходу при покупке 2-го предмета. Значит, П₁ покупает первый предмет, если V₁  (p + d)  V₂   (c  p + d), т. е., p  (V₁  V₂ + c)/2. Аналогично рассуждая для П₂, получим, что он повысит цену, если p  (V_l  V₂ + b)/2. B случае, когда цена поднимется выше наименьшей из двух величин (V₁  V₂ + c)/2 и (V₁  V₂ + b)/2, предмет будет продан.

В случае b < с первый предмет будет куплен П₁ по цене p = (V₁  V₂ + b)/2. Его доход будет равен

Д₁ = (V₁  ((V₁  V₂ + b)/(2 + d)) = (V₁ + V₂ - b)/(2  d).

В случае с < b первый предмет будет куплен П₂ по цене р = (V₁  V₂ + с)/2. Доход Д₁ будет равен

Д₁ = V₂  (c  (V₁  V₂ + c)/(2 + d)) = (V₁ + V₂  c)/(2  d).

Сравним доходы, получаемые П₁ при двух рассмотренных стратегиях: максимизации разности доходов П₁ и П₂, максимизации своего дохода Д₁.

Д₁* = ((V₁ + V₂)/2  (b + c))/(4  d) и

Д₁** = ((V₁ + V₂  c)/(2  d).

Их разность Д₁*  Д₁** = b/4 + с/4.

Пример 18. Пусть исходные данные, как в примере 1, b = 2500 руб., с = 2200 pуб. V₁ = 1000 pуб., V₂ = 2000 руб. Тогда П₁ будет повышать цену на первый предмет до величины р = (1000  2000 + 2200)/2 = 600 руб., П₂ будет повышать цену на первый предмет до величины р = (1000  2000 + 2000)/2 = 500 руб. и 1-ый предмет купит П₁ за 500 руб., таким образом, его доход Д₁ = 1000  500 = 500 руб.

Пример 19. Пусть аукционные товары стоят соответственно 1500 руб. и 2000 руб., участники располагают суммами 2000 руб. Тогда: Д₁ = (1500 + 2000  2000)/2 = 750 руб. Значит, за первый товар П₁ как и П₂, предложит 750 руб., за второй — 1250 руб.