1.5 Классификация измерений

1.5.1 Вид измерений – часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин.

Измерения весьма разнообразны, что объясняется множеством измеряемых величин, различным характером их изменения во времени, различными требованиями к точности измерений и т.д.

В связи с этим измерения классифицируются по различным признакам (рисунок 1).

Равноточные измерения – ряд измерений какой-либо величины, выполненных несколькими одинаковыми по точности СИ в одних и тех же условиях с одинаковой тщательностью.

Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающими по точности СИ и (или) в разных условиях.

Однократное измерение – измерение, выполненное один раз. На практике во многих случаях выполняются однократные измерения, например, времени по часам, для производственных процессов.

Многократные измерения – измерение одного и того же размера ФВ, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящих из ряда однократных измерений.

Статические измерения – измерения ФВ, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.

23

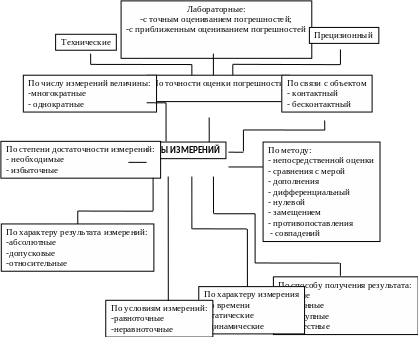
Рисунок 1 - Классификация видов измерения

Динамическое измерение – измерение изменяющейся по размеру ФВ. Результатом динамического измерения является функциональная зависимость измеряемой величины от времени, т. е. когда выходной сигнал изменяется во времени в соответствии с изменением измеряемой величины.

Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.

Например, измерение длины пути при равномерном прямолинейном равномерном движении L = vt, основано на измерении основной величины – времени Т и использовании физической постоянной v.

24

Понятие абсолютное измерение применяется как противоположное понятию относительное измерение и рассматривается как измерение величины в ее единицах. В такой трактовке это понятие находит все большее применение.

Относительное измерение – измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.

Относительные измерения при прочих равных условиях могут быть выполнены более точно, так как в суммарную погрешность результата измерений не входит погрешность меры ФВ.

Примеры относительных измерений: измерение отношений мощностей, давлений и т.д.

Метрологические измерения – измерения, выполненные с использованием эталонов.

Технические измерения – измерения, выполненные техническими СИ.

1.5.2 Прямое измерение – измерение ФВ, проводимое прямым методом, при котором искомое значение ФВ получают непосредственно из опытных данных.

Прямое измерение производится путем сравнения ФВ с мерой этой величины непосредственно или путем отсчета показаний СИ по шкале или цифровому прибору, градуированных в требуемых единицах.

Часто под прямыми измерениями понимаются измерения, при которых не производятся промежуточных преобразований.

Примеры прямых измерений: измерение длины, высоты с помощью линейки, напряжения – с помощью вольтметра, массы с помощью пружинных весов.

Уравнение прямого измерения имеет следующий вид:

Q = q[Q].

Косвенное измерение – измерение, полученное на основе результатов прямых измерений других ФВ, функционально связанных с искомой величиной известной зависимостью.

Уравнение косвенных измерений имеет следующий вид:

Y = F(x₁, x₂…, x_i,… x_n),

Y = F(x),

где F – известная функция;

n – число прямого измерения ФВ;

x₁, x, x_i, x_n – значения прямого измерения ФВ.

Например, определение площади, объема с помощью измерения длины, ширины, высоты; электрической мощности методом измерения силы тока и напряжения и т. д.

Совокупные измерения – одновременно проводимые измерения нескольких одноименных величин, при которых искомое значение величины, определяют путем решения системы уравнений, получаемых при измерениях различных сочетаний этих величин.

25

Понятно, что для определения значений искомых величин число уравнений должно быть не меньше числа величин.

Пример: значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений ) масс различных сочетаний гирь.

Имеются гири массами m₁, m_2, m₃.

Масса первой гири определится следующим образом:

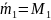
Масса второй гири определится как разность массы первой и второй гирь М_1,2 и измеренной массой первой гири m₁:

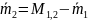
Масса третьей гири определится как разность массы первой, второй и третьей гирь М_1,2,3 и измеренных масс первой и второй гирь

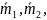
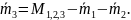
Часто именно этим путем добиваются повышения точности результатов измерения.

Совместные измерения – одновременно проводимые измерения нескольких неодноименных ФВ для определения зависимости между ними.

Пример1. Построение градуировочной характеристики Y = f(x) измерительного преобразователя, когда одновременно измеряют наборы значений:

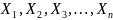
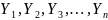
Значение ФВ определяется с помощью СИ конкретным методом.