1.12 Понятие абсолютной, относительной и приведенной погрешностей

Погрешности измерений появляются из-за несо­вершенства применяемых методов и средств измерений, непос­тоянства влияющих на результат измерения внешних условий, физических величин и индивидуальных особенностей экспериментатора.

Признаки, по которым принято классифицировать погрешности измерений, показаны на рисунке 3.

Абсолютная погрешность измерения Δх - по­грешность измерения, выраженная в единицах измеряемой величины.

Фактически термин «абсолютная погрешность» адекватен термину «погрешность результата измерения», также определяют соотноше­нием (1).

Относительная погрешность измерения - по­грешность измерения, выраженная отношением абсолютной погреш­ности измерения к действительному или измеренному значению из­меряемой величины.

Относительную погрешность в долях или процентах находят из отношений

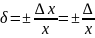или в процентах 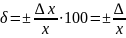∙100,

где Δх = Δ - абсолютная погрешность измерений.

Приведенная погрешность СИ γ - относительная погрешность, выраженная отношением абсолютной погрешности средства измерений Δ_СИ к условно принятому значению величины Х_N , постоянному во всем диапазоне измерений или в части диапазона

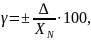
38

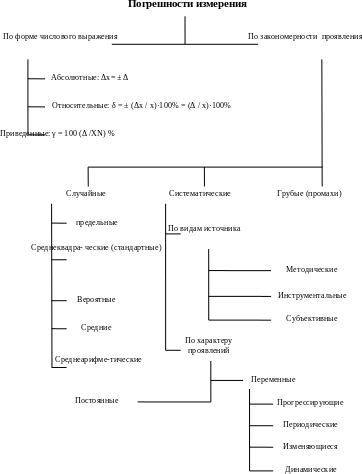
Рисунок 3 - Классификация погрешностей измерений

39

где γ - приведенная погрешность, %;

Х_N – нормирующее значение ФВ.

Часто за нормирующее значение принимают верх­ний предел измерений или сумму значений шкал при двусторонней шкале.

Пример выражения результатов измерения в единицах измеряемой ФВ при отсчете по шкалам приборов, на которых указана относительная или приведенная погрешности.

Отсчет по шкале прибора с пределами измерений 0 – 50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешности измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ класса точности:

0,02 / 0,01; 0,5 и 0,5.

Решение. 1. Для СИ класса точности 0,02 / 0,01 δ = Δ/х = ± [c + d (| x_к / х| - 1)].

Так как х = 25, x_к = 50, с = 0,02, d = 0,01 и δ дано в процентах, то

δ = ± [0,02 + 0,01(| 50 / 25| - 1)] = ± 0,03%; Δ = ± δ∙ х/100 = ±( 0,03∙25/100) = ± 0,0075 А.

2. Для СИ класса точности 0,5

δ = ± Δ / х; Δ = ± 0,01∙ δ∙ х = ± 0,01∙0,5∙25 = ± 0,125 А.

3. Для СИ класса точности 0,5

γ = ± (Δ / х_N), где х_N = 50, тогда Δ = ± 0,01∙50∙0,5 = 0,25 А.

1.13. Погрешность измерений. Систематическая составляющая погрешности измерений.

1.13.1 Погрешность результата измерений (погрешность измерения) - отклонение результата измерения от истин­ного (действительного) значения измеряемой величины.

Истинное значение физической величи­ны неизвестно и его применяют лишь в теоретических исследованиях и расчетах. На практике используют действительное значение ФВ х_д ~ х_и , в результате чего погрешность измерения Δх_изм определяют по формуле

Δх_изм= х_изм - х_д ,

где х_изм - измеренное значение величины (х_д ~ х_и).

В качестве истинного значения при многократных изме­рениях параметра выступает

среднее арифметическое зна­чение х

х_и = х_ср = .

40

1.13.2 Систематическая погрешность – это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины. Обычно систематическую погрешность пытаются исключить возможными способами (например, применением методов измерения, снижающих вероятность ее возникновения), если же систематическую погрешность невозможно исключить, то ее просчитывают до начала измерений и в результат измерения вносятся соответствующие поправки.

В процессе нормирования систематической погрешности определяются границы ее допустимых значений.

Систематическая погрешность определяет правильность измерений средств измерения (метрологическое свойство).

Систематические погрешности в ряде случаев можно определить экспериментальным путем. Результат измерений тогда можно уточнить посредством введения поправки.

Поправка (С) - значение величины, которая одноименна с измеряемой, и вводится в

неисправленный результат измерения с целью устранения неисключенных составляющих

сис­тематической погрешности.

Знак поправки противоположен знаку погрешности: можно записать, что С = - Δ _с и тогда результат измерения х = х_д + Δ_с + С (численное значение С может быть как со знаком «+», так и со знаком «-»).

По­правку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.

Поправочный множитель - числовой коэф­фициент С_м, на который умножают неисправленный результат изме­рения для исключения влияния систематической погрешности измерений.

Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению измеряемой ФВ. Поправки и поправочные множители могут определять­ся теоретически или экспериментально, представляются в виде числа или функции, заданной графически, таблично или аналитическими выражениями.

1.13.3 Способы исключения систематических погрешностей делятся на четыре вида (а – б):

а) ликвидация причин и источников погрешностей до начала проведения измерений;

б) устранение погрешностей в процессе уже начатого измерения способами замещения, компенсации погрешностей по знаку, противопоставлениям, симметричных наблюдений;

в) корректировка результатов измерения посредством внесения поправки (устранение погрешности путем вычислений);

41

г) определение пределов систематической погрешности в случае, если ее нельзя устранить.

Ликвидация причин и источников погрешностей до начала проведения измерений.

Данный способ является самым оптимальным вариантом, так как его использование упрощает дальнейший ход измерений (нет необходимости исключать погрешности в процессе уже начатого измерения или вносить поправки в полученный результат).

Для устранения систематических погрешностей в процессе уже начатого измерения применяются различные способы:

- способ введения поправок базируется на знании систематической погрешности и действующих закономерностей ее изменения. При использовании данного способа в результат измерения, полученный с систематическими погрешностями, вносят поправки, по величине равные этим погрешностям, но обратные по знаку;

- способ замещения состоит в том, что измеряемая величина заменяется мерой, помещенной в те же самые условия, в которых находился объект измерения. Способ замещения применяется при измерении следующих электрических параметров: сопротивления, емкости и индуктивности;

- способ компенсации погрешности по знаку состоит в том, что измерения выполняются два раза таким образом, чтобы погрешность, неизвестная по величине, включалась в результаты измерений с противоположным знаком;

- способ противопоставления похож на способ компенсации по знаку. Данный способ состоит в том, что измерения выполняют два раза таким образом, чтобы источник погрешности при первом измерении противоположным образом действовал на результат второго измерения.

1.13.4 Определение неисключенной систематической погрешности. Если систематические погрешности невозможно исключить, то дают оценку доверительных границ неисключенной составляющей погрешности (НСП).

НСП результата измерения образуется из составляющих НСП метода, СИ или других источников. Например, приведенная погрешность СИ и неточность изготовления – неисключенные систематические погрешности.

В качестве границ составляющих НСП принимают, например, пределы основных и дополнительных погрешностей СИ, если случайные составляющие погрешности пренебрежимо малы.

При оценке границ НСП их рассматривают как случайные величины, распределенные по равномерному закону.

Границы неисключенной систематической погрешности θ при числе слагаемых т ≤ 3 вычисляют по формуле

42

θ = ± (3)

где θ_i - граница i-й составляющей неисключенной систематической погрешности.

При числе неисключенных систематических погрешностей т ≥ 4 вы­числения проводят по формуле

θ = ± k (4)

где k — коэффициент зависимости отдельных неисключенных систематических погрешностей от выбранной доверительной вероятности Р_д при их рав­номерном распределении (при Р_д = 0,99 k =1,4; при Р_д = 0,95 k =1,1).

Здесь θ рассматривается как доверительная квазислучайная (т. е. почти случайная) погрешность.