9 Выполнение лабораторной работы «Синтез управляющих автоматов»
9.1 Цель работы
Целью лабораторной работы является закрепление навыков проектирования цифровых автоматов на примере автомата Мура.
Отчет о работе представляется в виде текстового файла и пересылается диспетчеру дистанционного обучения.
9.2 Общие сведения об управляющих автоматах
При реализации цифровых устройств используется несколько путей их построения. Прежде всего, используется принцип декомпозиции задачи (структурная, функциональная, принципиальная схемы), когда устройство удается представить в виде совокупности более простых узлов, реализуемых на стандартных микросхемах комбинационного типа. Такой принцип обладает универсальностью и дает хорошие результаты при построении относительно несложных цифровых устройств.
Для построения широкого класса цифровых устройств, работа которых состоит в выполнении упорядоченной последовательности определенных операций над поступающими данными, целесообразно использовать принцип микропрограммного управления. При этом любая операция, реализуемая устройством, рассматривается как сложное действие, которое разделяется на последовательность элементарных действий — микроопераций, выполняемых в течение каждого такта. Для управления порядком следования микроопераций используется логическое условие Х, принимающее в зависимости от результата выполнения микроопераций значение единицы или нуля. Процесс выполнения операций в устройстве описывается в форме алгоритма, называемого микропрограммой.
При использовании описанного принципа принято делить цифровое устройство на две части (рис. 9.1): операционный блок (ОБ) и управляющий блок (УБ). ОБ предназначен для хранения поступающей информации I, выполнения заданного набора микроопераций, выработки значений логических условий Х и выходных сигналов U.
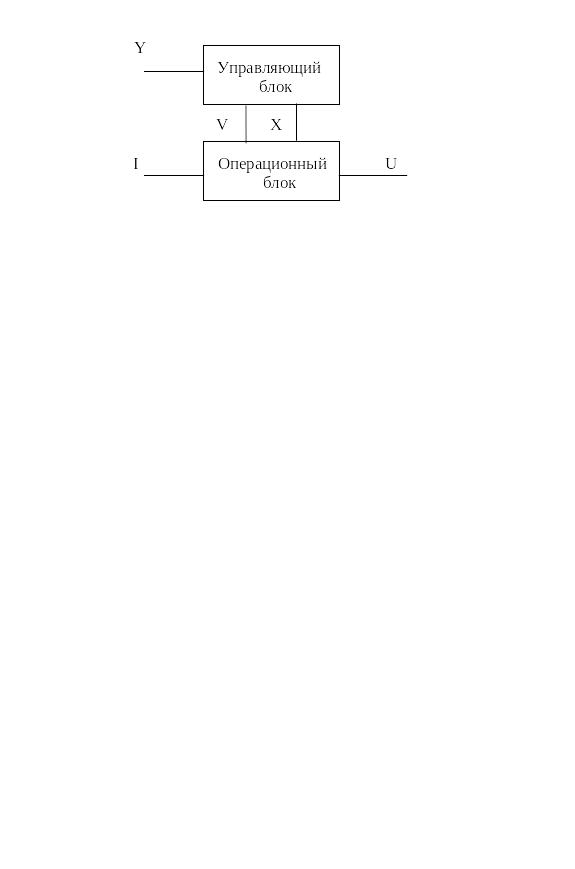
Рис. 9.1 — Представление цифрового устройства
в виде операционного и управляющего автоматов
УБ генерирует последовательность управляющих сигналов V в соответствии с заданной микропрограммой, оповестительными сигналами Х, поступающими от ОБ, и внешними сигналами Y, поступающими от оператора или цифрового устройства более высокого ранга.
Управляющий автомат можно реализовать на «жесткой» логике, когда используется чисто аппаратный подход к реализации устройства, и на «хранимой в памяти» логике, когда используется аппаратно-программный подход, чаще всего с использованием микропроцессорных средств.
В данной лабораторной работе закрепляются методы синтеза так называемых автоматов Мура, реализуемых на «жесткой логике» в виде памяти на D-триггерах, фиксирующих необходимое число внутренних состояний автомата, и комбинационных схем входной и выходной логики (рис. 9.2).
Рис. 9.2. — Структурная схема управляющего автомата:
М — память; DC — дешифратор состояний
9.4 Пример синтеза автомата Мура
Предположим, что необходимо спроектировать управляющий автомат, микропрограмма которого приведена на рис. 9.3.
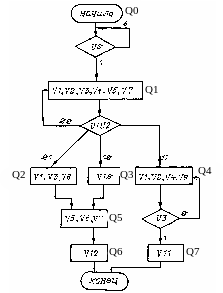
Рис. 9.3
Синтез микропрограммного автомата по микропрограмме осуществляется в два этапа.
На первом этапе на микропрограмме обозначаются состояния, выходные и входные сигналы.
Затем строится граф автомата Мура или Мили. Граф микропрограммного автомата приведен на рисунке 9.4.
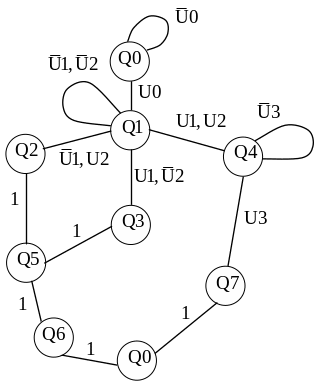
Рис. 9.4 — Граф автомата
На рисунке 9.4 обозначено: Q0 — исходное состояние автомата, которое должно устанавливаться при включении питающего напряжения и после обработки микропрограммы.
Рассматриваемый
автомат, находясь в исходном состоянии
Q0, ожидает появления входного сигнала
U0. Пока сигнала U0 нет, автомат не меняет
своего состояния. На это указывает петля
на графе не U0. Так как сигнал
0
является пусковым, то при появлении
последнего автомат переходит из состояния
Q0 в состояние Q1, при этом вырабатываются
выходные сигналы V1, V2, V3, V4, V5, V7. Далее
происходит ветвление в зависимости от
входных сигналов U1
и U2.
Причем если U1 и U2
равны нулю, автомат не меняет своего
состояния и находится в состоянии Q1.
При U1, равном нулю, и U2, равном единице,
автомат переходит в состояние Q2,
и вырабатываются выходные сигналы V1,
V3, V8.
Аналогично состоянию Q3 соответствует
выходной сигнал V10,
Q4
— V1,
V2, V4, V9
и т.д. Из состояния Q4 в состояние Q7
происходит условный переход в зависимости
от состояния входного сигнала U3. Если
сигнал U3 отсутствует, автомат не меняет
своего состояния и при появлении сигнала
переходит в состояние Q7. Переход из
состояния Q5 в состояние Q6
безусловный, и осуществляется он под
воздействием тактового импульса. Также
безусловный переход происходит из
состояния Q6
и Q7
в состояние Q0. Конец и начало означают
одно и то же состояние автомата —
исходное.
Теперь мы имеем все данные для построения автомата: определены все входные и выходные сигналы, состояния и условия перехода из одного состояния в другое. Рассматриваемый автомат имеет восемь состояний: с Q0 по Q7. Для фиксации и запоминания этих состояний автомат должен иметь специальную память соответствующей разрядности. Будем строить нашу память на D-триггерах. Эти триггеры и предназначены для построения памяти. Так как число состояний автомата восемь, то очевидно, что разрядность памяти для нашего случая будет равна трем. Обозначим состояния триггеров памяти, предназначенных для хранения состояний автомата, в виде таблицы 9.1.
Таблица 9.1
Состояние автомата |
Состояние триггеров |
||
Т1 |
Т2 |
Т3 |
|
Q0 |
0 |
0 |
0 |
Q1 |
0 |
0 |
1 |
Q2 |
0 |
1 |
0 |
Q3 |
0 |
1 |
1 |
Q4 |
1 |
0 |
0 |
Q5 |
1 |
0 |
1 |
Q6 |
1 |
1 |
0 |
Q7 |
1 |
1 |
1 |
В таблице двоичное представление состояния автомата соответствует десятичному индексу, но код состояния может быть выбран произвольным.
Построим выходную часть автомата, которая формирует выходные сигналы. Очевидно, схема должна содержать три D-триггера, дешифратор и соответствующую логику формирования выходных сигналов. Логика строится следующим образом: если сигнал управления V1 должен формироваться при состояниях Q1, Q2, Q4, то можно записать, что V1 = Q1 + Q2 + Q4 и соответственно для других сигналов:
V2 = Q1 + Q4 V7 = Q1 + Q5
V3 = Q1 + Q2 V8 = Q2
V4 = Q1 + Q4 V9 = Q4
V5 = Q1 + Q5 V10 = Q3
V6 = Q5 V11 = Q7
V12 = Q6
Схема формирования сигналов управления показана на рисунке 9.5.
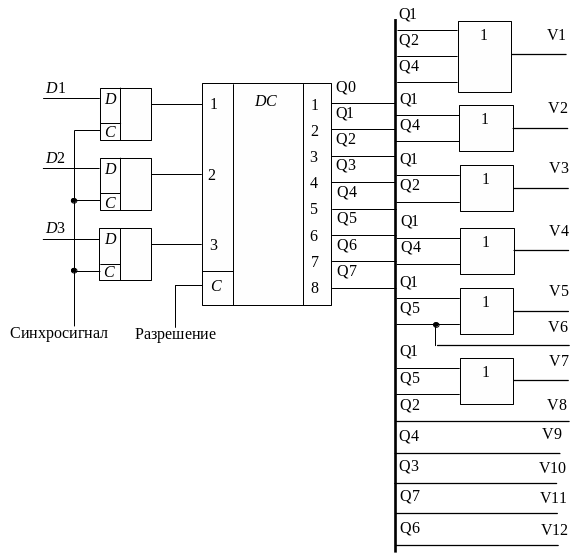
Рис. 9.5
На следующем этапе необходимо построить логическую схему, позволяющую обеспечить нормальный переход триггеров памяти в нужное состояние, обеспечив тем самым соответствующее состояние автомата. Для построения необходимо знать состояние каждого триггера для каждого состояния автомата (см. табл. 9.1), последовательность состояний (согласно алгоритму), условия перехода из одного состояния в другое. По имеющимся этим данным строим таблицу переходов, в которой для каждого перехода (см. граф автомата) необходимо вписать:
состояние автомата до перехода;
соответствующее этому состоянию состояние триггеров памяти;
состояние триггеров после перехода;
сигналы, обеспечивающие переход, а в случае нескольких сигналов — конъюнкции этих сигналов, представляющих собой условия перехода.
Алгоритм построения таблицы следующий.
В левой графе «Исходное состояние» указывается исходное состояние автомата, предшествующее переходу. В следующих колонках «Исходное состояние триггеров» указывается состояние триггеров, соответствующих данному состоянию автомата. В колонках «Состояние триггеров после перехода» указывается состояние триггеров, соответствующих состоянию автомата после перехода. В следующей колонке записывается условие перехода автомата из предыдущего состояния в последующее. Если переход по условию, то записывается состояние входных сигналов, позволяющих делать тот или иной переход, а если переход безусловный, т.е. входные сигналы не участвуют в организации перехода, то в данной колонке ставится единица. В следующих колонках записываются значения сигналов на D-входах триггеров памяти автомата. Так как у D-триггеров состояние на D-входах с приходом сигнала синхроимпульса переписывается на выход триггера, то колонки «Состояние триггеров после перехода» и «Состояние на D-входах» совпадают. После составления таблицы анализируем колонки «Состояние входов триггеров» и выбираем строки, в которых входные сигналы триггеров имеют единичное значение для каждого входа и записываем функции возбуждения при помощи уравнений.
По исходной схеме автомата, содержащей состояния и условия перехода (рис. 9.3), составим таблицу переходов (табл. 9.2):
Таблица 9.2 — Таблица переходов
Исходное состояние |
Состояние после перехода |
Условие перехода |
Состояние входов триггеров |
||
D3 |
D2 |
D1 |
|||
Q0 |
Q0 |
неU0 |
0 |
0 |
0 |
Q0 |
Q1 |
U0 |
0 |
0 |
1 |
Q1 |
Q1 |
неU1*неU2 |
0 |
0 |
1 |
Q1 |
Q2 |
неU1*U2 |
0 |
1 |
0 |
Q1 |
Q3 |
U1*неU2 |
0 |
1 |
1 |
Q1 |
Q4 |
U1*U2 |
1 |
0 |
0 |
Q2 |
Q5 |
1 |
1 |
0 |
1 |
Q3 |
Q5 |
1 |
1 |
0 |
1 |
Q4 |
Q4 |
неU3 |
1 |
0 |
0 |
Q4 |
Q7 |
U3 |
1 |
1 |
1 |
Q5 |
Q6 |
1 |
1 |
1 |
0 |
Q6 |
Q0 |
1 |
0 |
0 |
0 |
Q7 |
Q0 |
1 |
0 |
0 |
0 |
Запишем функции возбуждения триггеров в дизъюнктивной нормальной форме:
D1 = Q0*U0+Q1*неU1*неU2+Q1*U1*неU2+Q2+Q3+Q4*U3;
D2 = Q1*неU1*U2+Q1*U1*неU2+Q5+Q4*U3;
D3 = Q1*U1*U2+Q2+Q3+Q5+Q4;
неU3+Q4*U3= Q1*U1*U2+Q2+Q3+Q5+Q4;
(неU3+U3)=1;
После записи функций возбуждения необходимо попытаться произвести минимизацию функций. По уравнениям строим схему возбуждения и полную схему автомата.
Функциональная схема автомата (с учетом логики переходов) представлена на рисунке 9.6:
, U0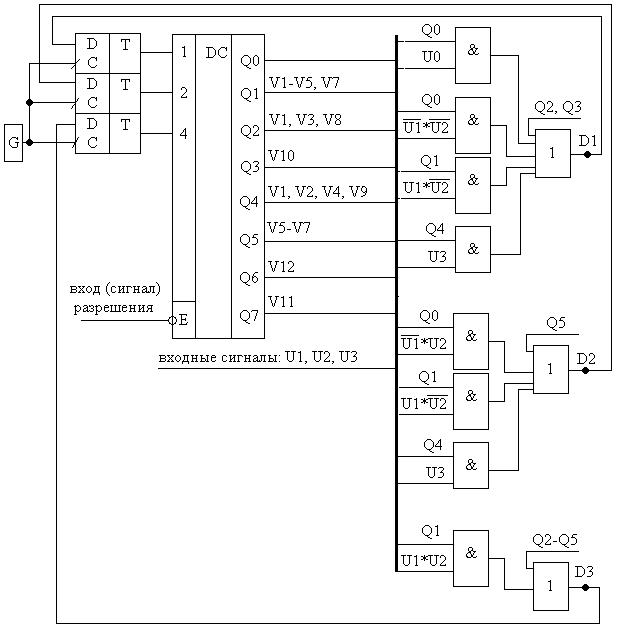
Рис. 9.6