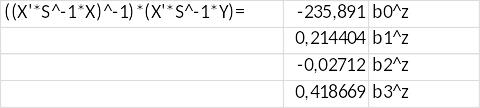Перевірка наявності гетероскедастичності( за параметричним тестом Гольдфельда-Квандта).
Припустимо, що зміну дисперсії залишків можуть викликати всі три змінні Z; Z’; Z”, тому проведемо тестування за цими трьома факторами:
Спостереження ранжуємо у порядку спаду значення відповідно до величини елементів вибраного нами вектора Z:
Відкинемо С спостережень, які знаходяться всередині векторів вихідних даних:
С= 6,4
Побудуємо дві моделі на основі МНК по двої створених сукупностях спостережень розмінрістю n-c/2=6, за умови що n-c/2>=m, де m=3- кількість змінних.
Знайдемо суму квадратів залишків S1 і S2 по першій та другій моделях
S1= 393,4021726 S2= 64,33512459
Значення критерію F= 0,163535255 порівняємо з табличним значенням Ft критерію при вибраному рівні довіри 0,05 і відповідних ступенях вільності: Ft=F(0,05;3;3)= 9,276628153. Так як F<Ft, то гетероскедастичність відсутня.
Отже, фактор Z не викликає гетероскедастичність залишків моделі.
Спостереження ранжуємо у порядку спаду значення відповідно до величини елементів вибраного нами вектора Z’:
Відкинемо С спостережень, які знаходяться всередині векторів вихідних даних:
С= 6,4
Побудуємо дві моделі на основі МНК по двої створених сукупностях спостережень розмінрістю n-c/2=6, за умови що n-c/2>=m, де m=3- кількість змінних.
Знайдемо суму квадратів залишків S1 і S2 по першій та другій моделях
S1= 40,75577941 S2= 289,3005944
Значення критерію F= 7,098394353 порівняємо з табличним значенням Ft критерію при вибраному рівні довіри 0,05 і відповідних ступенях вільності: Ft=F(0,05;3;3)= 2,714565112. Так як F>Ft, то гетероскедастичність присутня.
Отже, фактор Z’ викликає гетероскедастичність залишків моделі.
Спостереження ранжуємо у порядку спаду значення відповідно до величини елементів вибраного нами вектора Z”:
Відкинемо С спостережень, які знаходяться всередині векторів вихідних даних:
С= 6,4
Побудуємо дві моделі на основі МНК по двої створених сукупностях спостережень розмінрістю n-c/2=6, за умови що n-c/2>=m, де m=3- кількість змінних.
Знайдемо суму квадратів залишків S1 і S2 по першій та другій моделях
S1= 92,43706048 S2= 10,95505459
Значення критерію F= 0,118513662порівняємо з табличним значенням Ft критерію при вибраному рівні довіри 0,05 і відповідних ступенях вільності: Ft=F(0,05;3;3)= 9,276628153. Так як F<Ft, то гетероскедастичність відсутня.
Отже, фактор Z” не викликає гетероскедастичність залишків моделі.
Отже, фактор Z’ викликає гетероскедастичність залишків моделі, тому потрібно обчистили параметри моделі, використовуючи узагальнюючий метод Ейткена, вектор оцінювання якого має вигляд:
B=((X'*S^-1*X)^-1)*(X'*S^-1*Y)
Будуємо матрицю S. Оскільки явище гетероскедастичності пов’язане лише з тим, що змінюються дисперсії залишків, а коваріація між ними відсутня, то матриця S має бути діагональною.
Будуємо матрицю X для змінних Z, Z’, Z”.
Будуємо обернену матрицю X’ за допомогою функції ТРАНСП.
Знаходимо значення S^-1 за допомогою функції МОБР.
Знаходимо значення X'*S^-1 за допомогою функції МУМНОЖ.
Знаходимо значення X'*S^-1*X за допомогою функції МУМНОЖ.
Знаходимо значення (X'*S^-1*X)^-1 за допомогою функції МОБР.
Знаходимо значення X'*S^-1*Y за допомогою функції МУМНОЖ.
Отже, обчисливши параметри моделі за заданим рівнянням ми отримали такі результати:
