2 Основные расчеты

Функция W (θ, ψ), определяемая формулой (10) И входящая в правую часть уравнения (23), может быть разложена в ряд по шаровым функциям:

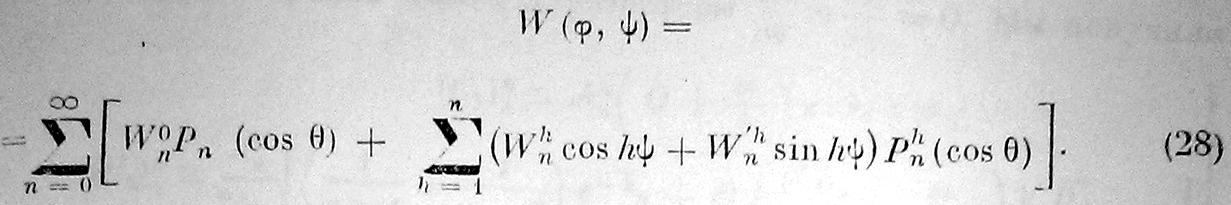
Будем искать и решение уравнения (23) так же в виде ряда па шаровым функциям:

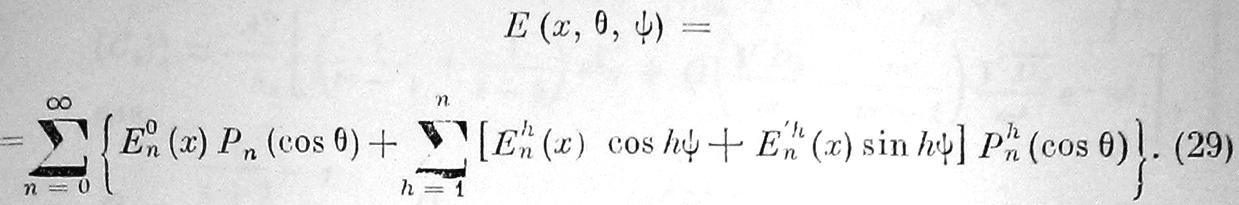
Подставляя эти ряды в уравнение (23), применяя уравнение, кото­рому удовлетворяют шаровые функции, и сравнивая коэффициенты, получим:

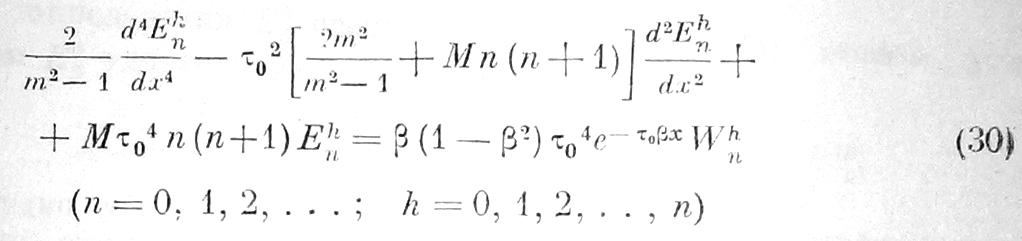
и такое же уравнение для Е’^h_n (с заменой W^k_n на W’^h_n, причем здесь

h = 1, 2, . .. , n). Уравнение (30) дает для всех Е^h_n (кроме Е⁰₀)

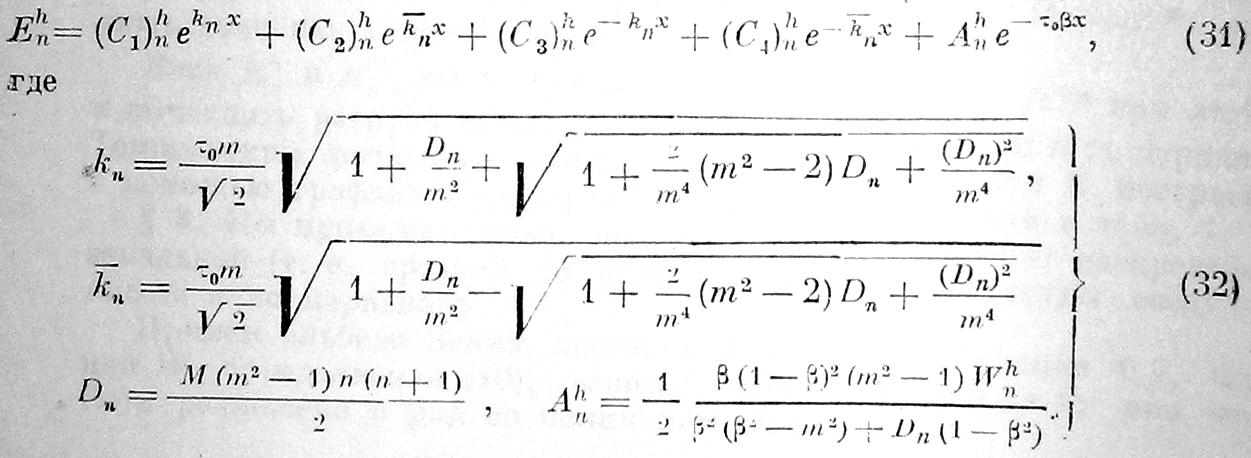
Мы приняли m=1,75; τ₀=12,6; β=0,2; q=1,15. При подсчёте величины 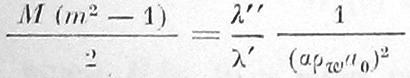мы положили λ”/ λ’равным 10⁶ [7], за α и ρ_w мы приняли их средние наземные значения: ρ_w=6,2*10^-6 г/см³, α = 7,25 см²/г [2] . При этом оказалось:

(M(m²-1))/2=0,00128,

и можно с большой точностью записать:

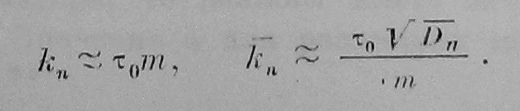
Постоянные (С₁)^h_n, (С₂)^h_n, (С₃)^h_n, (С₄)^h_n, входящие в (31), определяются из условий (24), (25), (26) и (27). При определении этих постоянных для всех E^h_n и E’^h_n, за исключением E⁰₀, мы приняли равенство нулю E^h_n, E’^h_n при х=0, что отвечает условию выравнивания температур в верхних слоях стратосферы дЕ/дθ = дЕ/дψ = 0. Мы получили:

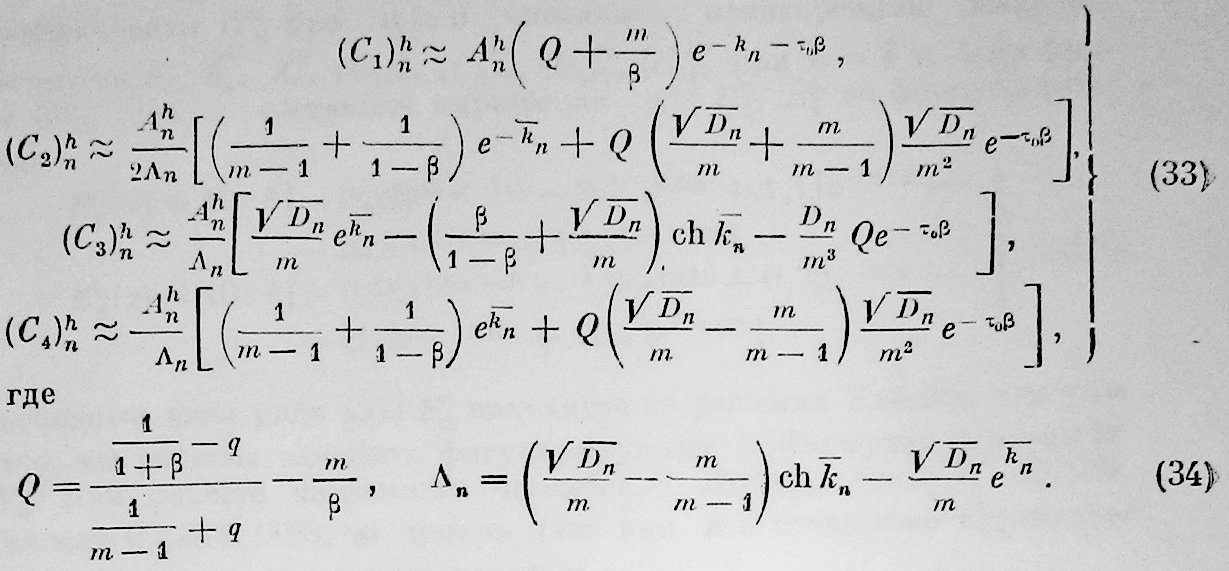
При определении Е⁰₀ следует принять из (25) второе условие. При этом Е⁰₀ удовлетворяет уравнению:

Нетрудно убедиться, что и краевые условия и дифференциальное уравнение, служащие для определения Е⁰₀, будут те яте, что служили в работе Кибеля [2] для определения ƒσТ⁴. Поэтому для получе­ния Е⁰₀ можно использовать уже готовое решение Кибеля (формулы (23) и (26) из работы [2]), нужно лишь заменить в нем W на W⁰₀.

Зная E^h_n и E’^h_n, мы можем построить ряд для Е = fσТ⁴ при любом х, и вычислить распределение Е по высоте, по параллели и по меридиану. Температуры легко определяются по таблице значений Е, построенной с помощью графика Гулъберта [5] для ƒ и приведенной в табл. 1.

3 Подсчет среднего годового распределения зональности температуры воздуха по высоте и по меридиану

Мы приведем здесь подсчет среднего годового распределения зональной (т. е. средней по всей параллели) температуры воздуха по высоте и по меридиану.

Примем альбедо Земли постоянной величиной, равной 0,7. Функция W, определяемая (10), зависит теперь только от θ; она может быть разложена в ряд по полиномам Лежандра:

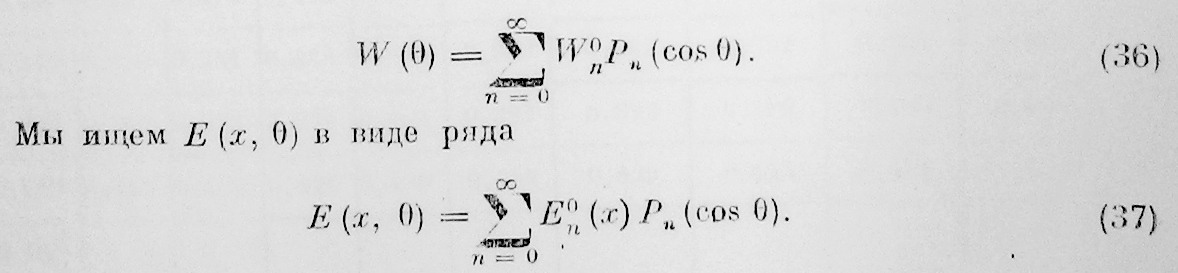
Так как среднее облучение на данной параллели W(θ) симметрично относительно экватора, то должны иметь место равенства W⁰₁= W⁰₃=W⁰₅=W…=0. Значит W для различных широт приведены в книге Миланковича [8] (вместе с Миланковичем мы принимаем солнечную постоянную равной 2 cal/см² мин).

Использовав эти значения W при вычислении коэффициентов ряда (36), мы получили:

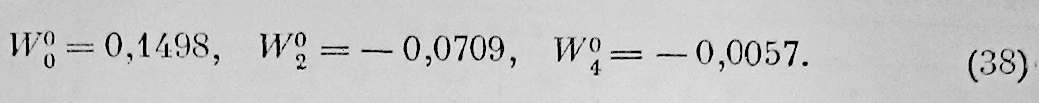
Коэффициенты W0n при n>6 оказались пренебрежительно малыми.

_

Вычисляя k_n, k_n , А⁰_n, (С₁)⁰_n, (С₂)⁰_n, (С₃)⁰_n, (С₄)⁰_n при n=2 и 4 по формулам (32), (33) и составляя выражения для Е⁰₂, Е⁰₄ по формуле (31), получим:

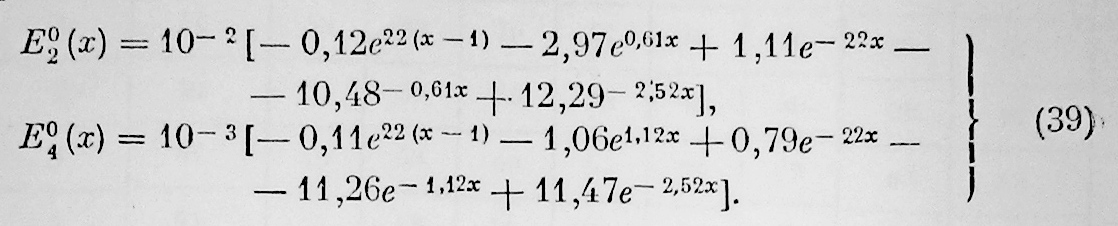
Свободный член ряда (37) Е⁰₀ находится из решения Кибеля; как уже сказано, мы должны заменить фигурирующее в формулах Кабеля W на W⁰₀. При расчете численного примера (формула (36) в работе [2]) Кибель взял W = 0,138.

Так как W⁰₀ = 0,1498, то теперь (так как все остальные параметры у Кибеля и у нас одинаковы), получим:

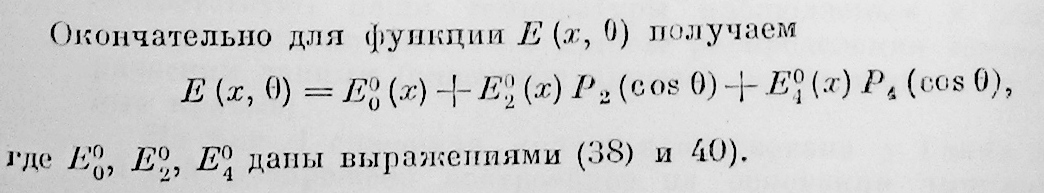
Эта формула принята нами для подсчета среднего годового распре­деления температуры воздуха по высоте и по меридиану; при этом нами использованы табл. 1 и соотношение:

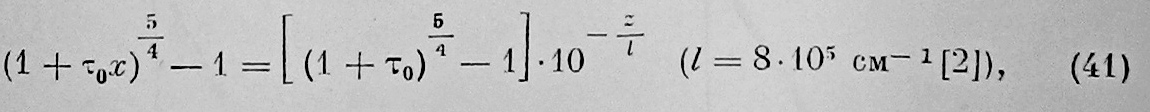
дающее связь между Х и Z.

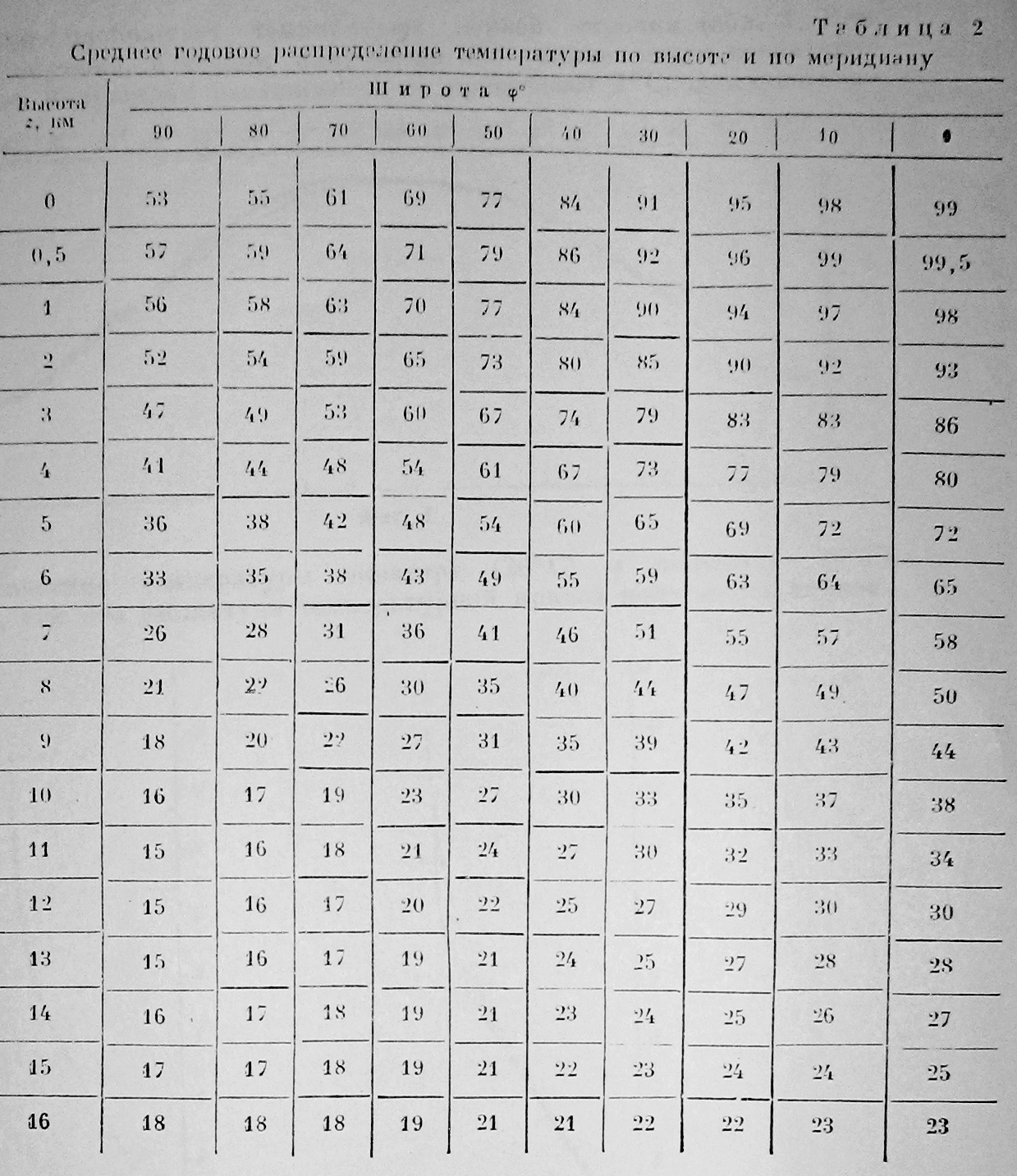
Распределение температуры по высоте в меридиану дается в табл. 2; для удобства температуры отсчитываются от 200°К; температуры даны в градусах Цельсия.