Глава 2. Динамика относительного движения материальной точки

2.1. Основные теоретические сведения

При анализе движения точки относительно неинерциальной системы отсчета, совершающей произвольное заданное движение, используют второй закон. При анализе движения точки относительно неинерциальной системы отсчета, совершающей произвольное заданное движение, используют второй закон Ньютона и теорему Кориолиса

	(2.8)
,

Силы не зависят от выбора системы отсчета. Тогда

Обозначая и , получаем

,

(2.9)

где называют соответственно переносной и кориолисовой силами инерции.

Следует напомнить, что

и ,

где – характеристики движения подвижной системы отсчета (подробнее об этом см. в методических указаниях «Теоретическая механика (кинематика)» стр. 12).

2.2. Последовательность составления и решения уравнений

Уравнения динамики относительного движения точки составляются также, как и в инерциальной системе отсчета (2.8), только при этом к действующим на точку силам следует добавлять переносную и кориолисову силы инерции. Величины можно рассматривать как поправки, которые должен ввести наблюдатель, находящийся в подвижной системе отсчета, при анализе движения точки.

1. Разложить «абсолютное» движение точки на относительное и переносное; выбрать неподвижную систему отсчета и подвижную систему отсчета, связанную с подвижной средой, совершающей переносное движение;

2. Записать начальные условия относительного движения точки;

3. Изобразить на рисунке силы , приложенные к материальной точке;

4. Определить ускорение точки в переносном движении , ускорение Кориолиса . Найти силы инерции переносную и кориолисову и добавить эти силы к силам , приложенным к точке;

5. Составить дифференциальные уравнения (2.9) относительного движения точки в проекциях на подвижные оси координат;

6. Проинтегрировать дифференциальные уравнения (2.9), определяя постоянные интегрирования по начальным условиям.

7. Из полученных зависимостей найти искомые величины.

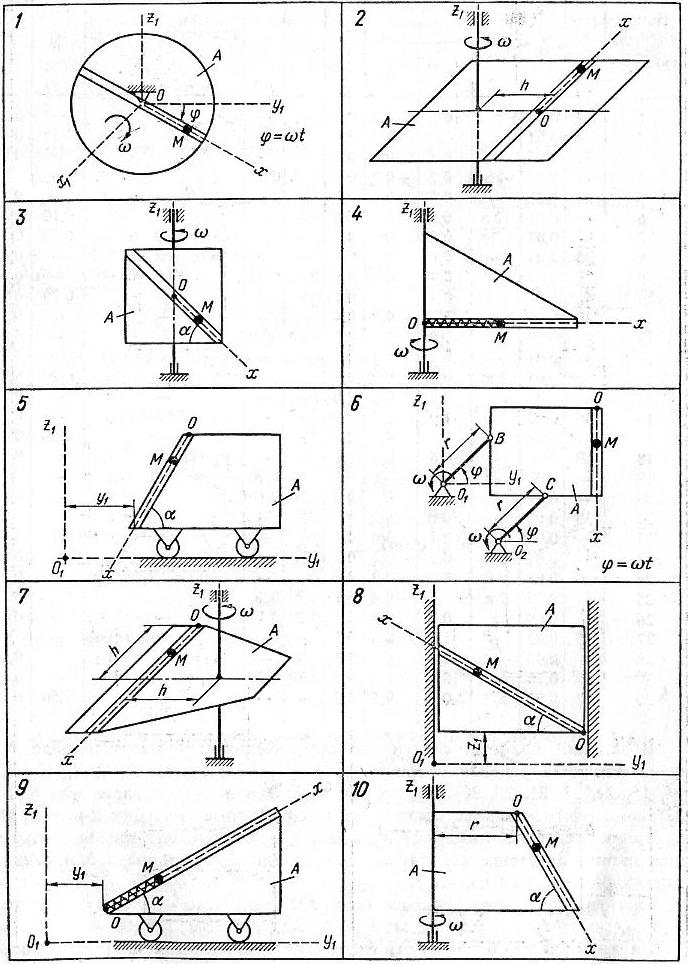
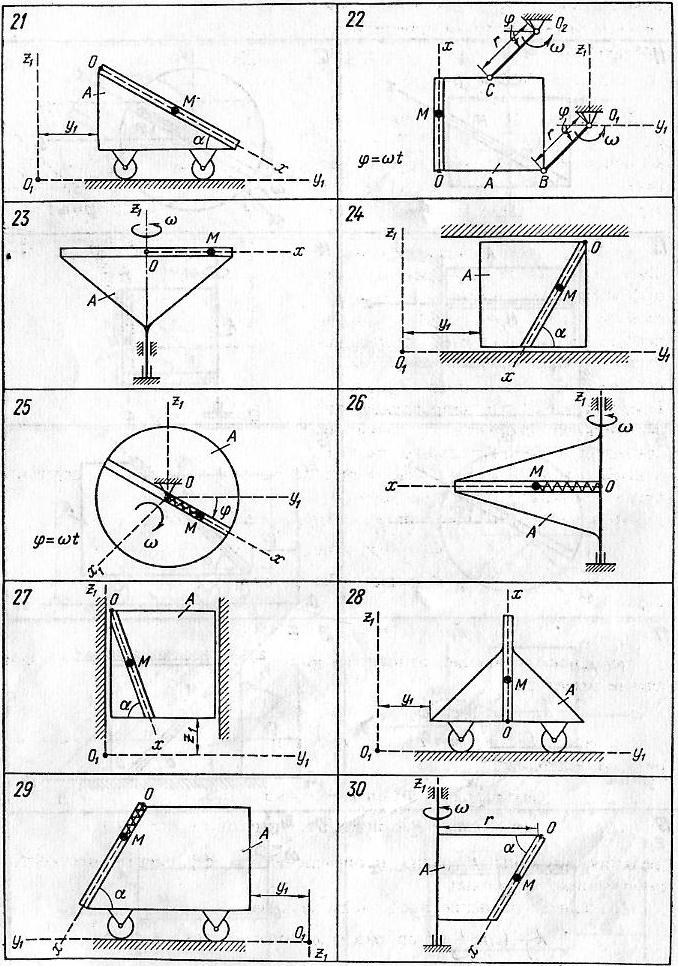
Задание. Шарик М, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела А (рис.8–10). Найти уравнение относительного движения этого шарика, приняв за начало отсчета точку О.

Тело А равномерно вращается вокруг неподвижной оси (в вариантах 2, 3, 4, 7, 10, 11, 14, 20, 23, 26 и 30 ось вращения z₁ вертикальна, в вариантах 1, 12, 15 и 25 ось вращения х₁ горизонтальна). В вариантах 5, 6, 8, 9, 13, 16, 17, 18, 19, 21, 22, 24, 27, 28 и29 тело А движется поступательно, параллельно вертикальной плоскости y₁O₁z₁.

Найти также координату х и давление шарика на стенку канала при заданном значении t = t₁. Данные, необходимые для выполнения задания, приведены в таблице. В задании приняты следующие обозначения: т – масса шарика М, ω –- угловая скорость тела А, с – коэффициент жесткости пружины, к которому прикреплен шарик М, l₀ – длина недеформированной пружины, f – коэффициент трения скольжения шарика по стенке канала, – начальная координата и проекция начальной скорости на ось х.

Рис. 8

Рис. 9

Рис. 10

Пример выполнения задания

Дано: α = 30⁰, ω = π рад/с, m = 0.01 кг, t₁ = 0.2 с, = 0.3 м, = 2 м/с, с = 1 Н/м, l₀ = 0.2 м, r = 2 м.

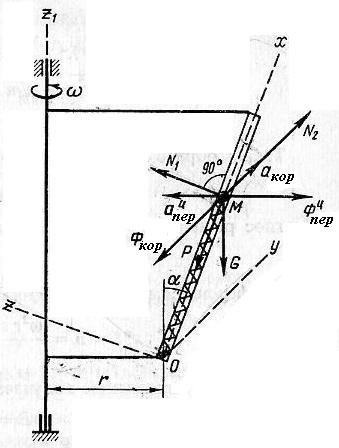
Рис. 11	Решение. Относительным движением шарика является его движение вдоль трубки. Совместим ось х с траекторией относительного движения шарика. Ось х является подвижной системой отсчета. Вращение этой системы вокруг оси z1 является переносным движением для шарика М. Относительное движение точки определяется уравнением
		(3.0)
	К шарику приложены силы: вес , реакция пружины , нормальная реакция стенки трубки, которую можно разложить на две взаимно перпендикулярные составляющие N1 и N2.

Присоединяем к силам, действующим на шарик переносную центробежную силу инерции и кориолисову силу инерции , направленные противоположно ускорениям . Направление ускорения найдем по правилу векторного умножения векторов. Предположим, что направление относительной скорости точки М совпадает с положительным направлением оси х. Вектор угловой скорости направлен по оси z1. В этом случае кориолисова сила инерции перпендикулярна плоскости этих векторов хОz и направлена в противоположную сторону ускорения , как показано на рис. 11.

Модули сил инерции определяются по формулам

,

где , .

Основное уравнение относительного движения точки М в данном случае имеет вид

.

(3.1)

Составим дифференциальное уравнение относительного движения шарика М вдоль оси х:

.

(3.2)

С учетом того, что реакция пружины равна произведению коэффициента жесткости на деформацию пружины получим

.

Последнее уравнение перепишем в виде

или

,

где , .

Общее решение полученного дифференциального уравнения имеет вид

,

где – общее решение соответствующего однородного уравнения;

– частное решение уравнения.

Таким образом, общее решение однородного уравнения будем искать в виде

или ,

Частное решение находим в форме

Из дифференциального уравнения находим

.

Решение дифференциального уравнения относительного движения шарика М получает вид

.

(3.3)

Скорость этого движения

.

(3.4)

Постоянные с₁ и с₂ определяем, используя начальные условия:

При t = 0 .

Из (3.3) и (3.4) для t = 0 имеем:

; .

Откуда

; .

Окончательно уравнение относительного движения шарика М принимает вид

.

Скорость относительного движения шарика

.

Для определения составляющих реакции стенки трубки N₁ и N₂ при t = t₁ = 0.2 с выразим векторное уравнение (3.2) в проекции на оси y и z. Учитывая, что вектор перпендикулярен этим осям, получаем

, .

Из этих уравнений находим

,

Для получения числовых значений N₁ и N₂ необходимо получить координату и проекцию относительной скорости точки , соответствующие значению t₁ = 0.2 с:

Следовательно, составляющие реакции N₁ = 0.077 H и N₂ = 0.080 Н.

Реакция стенки трубки .

Искомое давление шарика М на стенки трубки по числовому значению равно найденному значению реакции N и направлено в противоположную сторону.

Вопросы для самоконтроля.

1.Какой модуль и какое направление имеют переносная и кориолисова силы инерции?

2. В чем заключается различие между дифференциальными уравнениями относительного и абсолютного движения?

3. Как определяются переносная и кориолисова силы инерции в различных случаях переносного движения (поступательного переносного и вращательного переносного)?

4. Какие системы отсчета называются инерциальными?

5. Каково условие относительного покоя материальной точки?