Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Волжская Государственная Академия Водного Транспорта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Гордлеева И.Ю.,Тарнопольская Т.И. Теоретическая...doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

4.1 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Вопросы для самоконтроля.

1. Сформулируйте II закон Ньютона (основное уравнение динамики точки), если на материальную точку действует система сил.

2. Какие уравнения динамики точки получают при координатном способе задания движения точки? При естественном способе задания движения точки?

3. Каковы две основные задачи динамики точки, которые решаются с помощью дифференциальных уравнений движения материальной точки?

4. Как определяются постоянные при интегрировании дифференциальных уравнений движения материальной точки?

1.5. Прямолинейные колебания точки

Под действием восстанавливающих сил тела могут совершать колебательное движение.

Восстанавливающие силы – это силы, величины которых зависят от отклонения тел от положения равновесия.

Теория колебаний – хорошо развитый раздел динамики, имеющий большое практическое значение при анализе колебаний (вибрации) зданий, сооружений, их виброзащите, при создании новой вибрационной техники т. д.

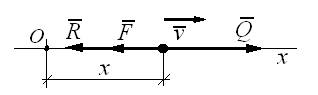
Схема сил

– восстанавливающая сила, – вязкое сопротивление среды

– возмущающая сила

Различают четыре случая колебательного движения материальной точки:

– собственные колебания;

– собственные колебания в среде с сопротивлением;

– вынужденные колебания;

– вынужденные колебания в среде с сопротивлением.

В данном методическом пособии рассматриваются только свободные колебания (собственные колебания с сопротивлением и без него). Для этих случаев в таблице 1.3 приведены дифференциальные уравнения и их общие решения.

Таблица 1.3

Вид колеб. и действ.силы

Дифференциальное

уравнение

Общее решение

Примечание

Свободные (Fx)

– частота гармонических колебаний

или

Постоянные интегрирования, находятся из начальных условий. А – амплитуда колебаний, – начальная фаза, - период свободных колебаний

Затухающие

(Fx, Rx)

–

коэффициент сопротивления

β<k

(малое сопротивление)

или

круговая частота колебаний с учетом сопротивления.

период затухающих колебаний, - декремент затухания (отношение любых последовательных максимальных отклонений точки в одну сторону)

β>k

(большое сопротивление)

В этом случае точка совершает апериодическое затухающее движение

β= k

(граничный случай)

Также случай апериодического затухания

Таблица 1.4

Обобщенные жесткости пружин

Параллельные пружины.

Для n параллельных пружин

Продолжение таблицы 1.4

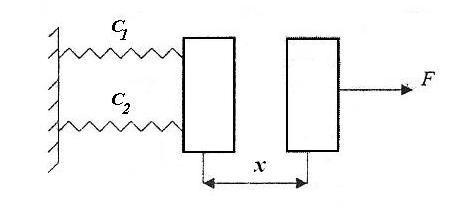
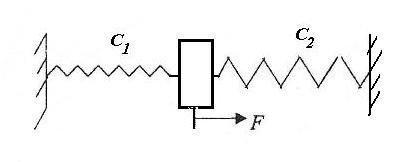
Тело между пружинами

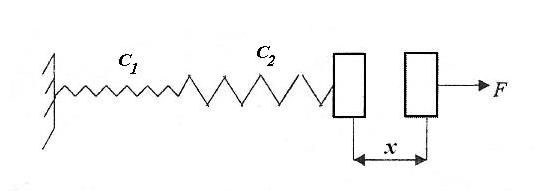
Последовательно соединенные пружины

Для n последовательных пружин

План решения задач.

1. Выбрать координатную ось, направив ее по направлению движения. Если в условии задачи не сказано о выборе начала координат, то его следует поместить в положение статического равновесия материальной точки.

2. Изобразить точку на оси в произвольном положении, но так, чтобы ее координата и скорость были положительны ( )

3. Изобразить все силы, действующие на точку.

4. Составить дифференциальное уравнение движения точки в проекции на выбранную ось и привести его к одному из видов, указанных в таблице 1.3.

5. Установить вид колебаний и для данного вида записать соответствующее общее решение.

6. Установить начальные условия движения, по ним определить постоянные интегрирования (т. е. константы с₁, с₂ или другие) и подставить их в решение.

Рис. 6

Примечание. При решении задач на колебательное движение точки целесообразно составлять расчетную схему, т. е. показать на рисунке следующие величины: l₀ – длину недеформированной пружины, λ_ст – статическое удлинение пружины, х – текущее положение точки от начала координат, О – положение статического равновесия точки.

Задание. Найти уравнение движения тела под действием восстанавливающей силы и силы сопротивления среды .

1		На пружине жесткостью 120 Н/см подвешено тело массой m₁= 2 кг. К нему присоединяют массу 4 кг и отпускают без начальной скорости. При дальнейшем движении на массы действует сила сопротивления R = 12v Н (v выражено в м/с) получить уравнение движения масс по оси Х, приняв начало отсчета в положении статического равновесия массы m₁.
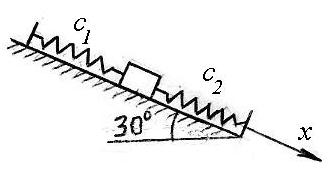
2		Деталь механизма массой 6 кг связана с двумя пружинами жесткостью 3 Н/м и 4 Н/м. в начальный момент она сдвинута вправо о положения статического равновесия и ей сообщена скорость v = 6 м/c, направленная так же вправо. Получить уравнение ее движения, выбрав начало отсчета в положении статического равновесия.
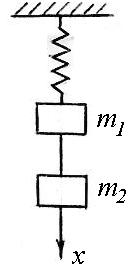
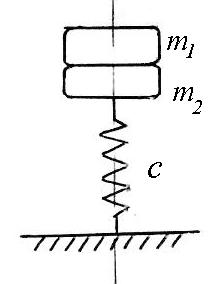
3		Две детали механизма массами m₁= 5 кг и m₂= =15 кг, соединенные невесомым стержнем и подвешенные к пружине, растягивают ее на Лст = 20 см. получить уравнение движения массы m₁, если вторая будет внезапно удалена (обрыв стержня). Начало координат принять в положении статического равновесия. Сила сопротивления при движении массы пропорциональна скорости: R = 10v (H, м/с).
4		Груз массой 2 кг падает с высоты 2 м на невесомую плиту, соединенную с пружиной, жесткостью 200 Н/м. Найти уравнение дальнейшего движения груза вместе с плитой. Начало координат принять в конце недеформированной пружины, во время движения учесть силу сопротивления R = 10v (H, м/с).
5		Деталь механизма массой 5 кг соединена с двумя пружинами жесткостями 4 Н/см и 6 Н/см и ей сообщена вниз скорость v = 5 м/c. Получить уравнение движения по оси х. Начало координат принять в положении статического равновесия груза.
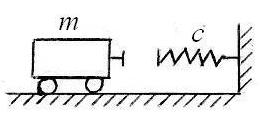
6		Платформа массой 20 т наезжает со скоростью 5 м/с на пружинный амортизатор жесткостью 2∙10³ кН/м и соединяется с ним. При дальнейшем движении на платформу действует сила сопротивления R = 40v (кH, м/с). Определить уравнение ее движения по оси х с началом в конце недеформированной пружины (трением пренебречь).
7		В механизме две детали массами m₁= 1 кг и m₂= 2 кг соединены невесомым стержнем и с пружиной, жесткостью 900 Н/м. Найти уравнение движения m₁ после внезапного удаления m₂(обрыв стержня), если сила сопротивления движению R = 12 v (H, м/с). Начало координат принять в положении статического равновесия m₁.
8		Тело массой 4 кг, подвешенное на двух пружинах жесткостью 6 и 4 Н/см, выведено из положения статического равновесия вниз на 2 см и отпущено без начальной скорости. Получить уравнение дальнейшего движения тела, если на тело действует сила сопротивления R = 6v (H, м/с). Начало координат принять в нижнем конце недеформированных пружин.
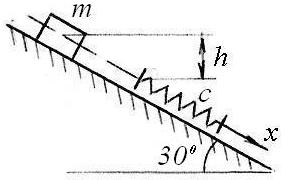
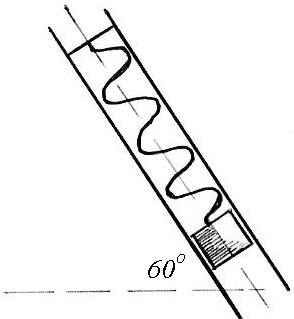
9		Тело массой 10 кг движется по гладким наклонным направляющим. Опустившись с высоты h = 2 м, оно соединяется с пружинными амортизаторами жесткостью 9 кН/м. Найти уравнение дальнейшего движения, отнеся его к оси х с началом в конце недеформированной пружины, если при движении действует сила сопротивления R = 20 v (H, м/с).
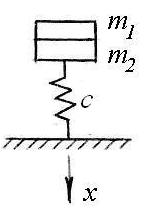
10		На пружинной рессоре жесткости 4.8 Н/см находятся в состоянии покоя два тела два тела. Тело массой m₁ снимают, и тело массой m₂приходит в движение, испытывая сопротивление R = 60 v (H, м/с). Получить уравнение тела m₂по оси х с началом в положении статического равновесия обоих тел.
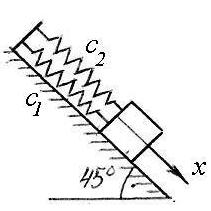
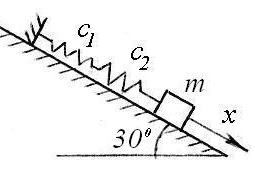
11		Тело массой 5 кг удерживается в равновесии на гладкой наклонной плоскости двумя пружинами жесткостями 3 и 6 Н/см. Тело выведено из положения равновесия на 5 см и отпущено без начальной скорости. Найти уравнение движения тела по оси х с началом отсчета в конце недеформированной пружины, учитывая силу сопротивления движению R = 50v (H, м/с).
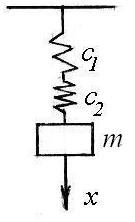
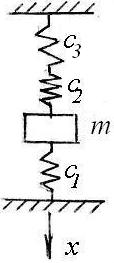
12		Тело массой 10 кг подвешено на трех пружинах жесткостями с₁= 5 Н/см, с₂= 2с₁, с₃= 3с₁. В начальный момент тело выведено из положения статического равновесия вниз на 5 см и отпущено без начальной скорости. Получить уравнение движения тела по оси х с началом в положении статического равновесия, если на тело действует сила сопротивления R = 4v (H, м/с).
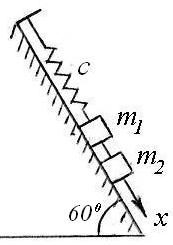
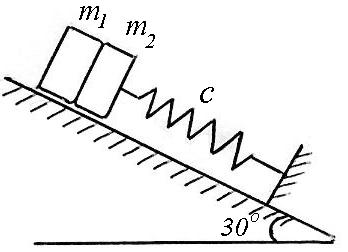
13		Два тела массами m₁= 2 кг и m₂= 3 кг, находятся на гладкой наклонной плоскости, опираясь на пружину жесткостью 6 Н/см. тело массой m₁ убирают, а тело массой m₂ начинает движение, испытывая сопротивление R = 60v (H, м/с). Получить уравнение движения тела m₂ с началом в положении статического равновесия обоих тел.
14		Поршень массой 4 кг соединен с пружиной жесткостью 4 Н/см и может двигаться по направляющим, испытывая сопротивление R = 24v (H, м/с). Длина недеформированной пружины 0.1 м, и поршень отпущен без начальной скорости. Получить уравнение движения поршня с началом отсчета в точке закрепления пружины (т. О). Трением пренебречь.
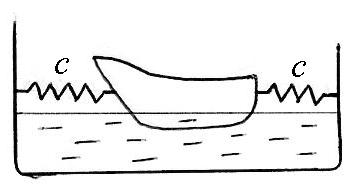
15		При движении модели судна сила сопротивления воды пропорциональна первой степени скорости R = 24v (H, м/с). Модель соединена с двумя одинаковыми пружинами, выведена из положения равновесия на 0.1 м и отпущена без начальной скорости. Получить уравнение движения модели с началом в положении равновесия, если через 5 колебаний амплитуда уменьшилась в 10 раз. Период колебаний Т = 0.5 с.
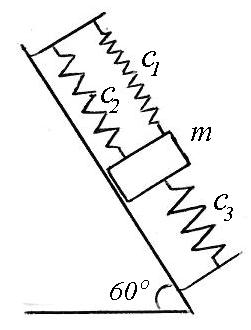
16		Тело массой 6 кг соединено с тремя пружинами и может двигаться по наклонным направляющим, испытывая при этом сопротивление движению R = = 120 v (H, м/с). Жесткости пружин: с₁= 5 Н/см, с₂= = 2с₁, с₃= 3с₁. В начальный момент тело выведено из положения статического равновесия вниз на 10 см в сторону возрастания координаты х и отпущено без начальной скорости. Получить уравнение движения тела по оси х с началом в положении статического равновесия, если на тело действует сила сопротивления R = 4v (H, м/с).
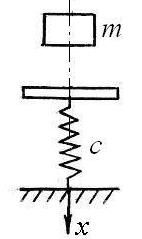
17		Тело массой 20 кг устанавливается на невесомую пластину, соединенную с пружиной жесткостью 20 Н/см. Сила сопротивления движению равна R = 200v (H, м/с). Найти уравнение движения тела. Начало координат принять в т. О – в конце недеформированной пружины.
18		Тело массой 20 кг находится в равновесии на пружинной рессоре, статическая деформация которой при этом равна 2 см. На это тело устанавливается второе массой 10 кг, и системе сообщается начальная скорость, направленная вниз. При движении тела испытывают R = 60 v (H, м/с). Получить уравнение движения тел, приняв начало координат в положении статического равновесия обоих тел.
19		Тело массой m соединено с пружиной и колеблется при отсутствии сопротивления с периодом Т = 0.4π (с). Получить уравнение движения тела, если в начальный момент оно было выведено из положения равновесия на 10 см и ему сообщена скорость 2 м/с, вектор которой направлен в сторону смещения тела
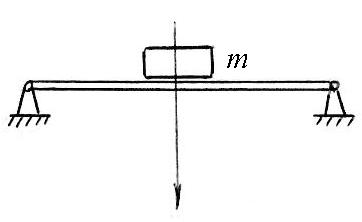
20		Груз массой 20 кг положен на невесомую балку без начальной скорости. Сила упругости балки пропорциональна прогибу F = cx Н, где с = 6 Н/см. Сила сопротивления движению R = 20 v (H, м/с). Получить уравнение движения груза по оси х. Начало координат принять в положении статического равновесия груза.
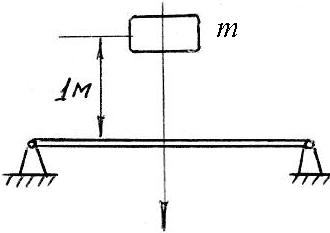
21		Груз массой 2 кг падает на невесомую балку с высоты 1 м и начинает колебаться вместе с ней. Сила упругости балки пропорциональна прогибу F = cx Н, где с = 40 Н/м. Сила сопротивления движению R = 10v (H, м/с). Получить уравнение движения груза по оси х, приняв за начало координат горизонтальное положение балки (без прогиба).
22		Два груза m₁= 4 кг и m₂= 6 кг находятся в равновесии на невесомой балке и прогибают ее на 2 см. Груз m₁ внезапно снимают, а груз m₂ начинает колебаться. Найти уравнение движения m₂, приняв начало отсчета в положении равновесия обоих тел. Сила упругости балки пропорциональна ее прогибу и равна F = 10x (Н), а сила сопротивления, возникающая при движении R = 60 v (H, м/с).
23		Невесомую балку с грузом массой 20 кг прогнули на 4 см и отпустили. Груз стал колебаться с периодом колебаний Т = 0.8π (с) и через 10 колебаний амплитуда уменьшилась в 10 раз. Получить уравнение движения груза, если сопротивление движению R = μv (H, м/с).
24		Груз массой 5 кг подвешен к концу нерастянутой пружины жесткостью с = 500 Н/см и отпущен без начальной скорости. Сила сопротивления движению R = μv (H, м/с). После 20 колебаний амплитуда уменьшается в 20 раз. Найти уравнение движения груза с началом отсчета в положении статического равновесия груза.
25		Груз массой m падает со скоростью 0.5 м/с на невесомую плиту, опирающуюся на пружину. Найти уравнение дальнейшего движения тела при учете силы сопротивлении движению пропорциональной скорости. Собственная круговая частота к = 10 с^-1, декремент затухания е^-ⁿ^Т= 0.2. Начало координат в положении статического равновесия.
26		Тело массой m подвешено к концу недеформированной пружины жесткостью с и получило начальную скорость v₀, направленную вверх. Найти уравнение движения тела по оси с началом в конце недеформированной пружины, а также время, в течение которого тело впервые пройдет через положение равновесия.
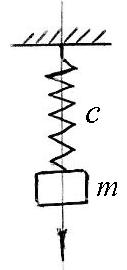
27		Тела массой 5 кг соединено с пружиной жесткостью 25 Н/м и может двигаться по горизонтальной плоскости. В начальный момент тело смещено из положения недеформированной пружины на 0.5 м и отпущено без начальной скорости. Найти уравнение движения тела, если при движении на него действует сила сопротивления R = 0.8 v H.
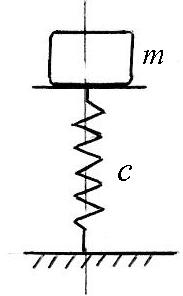
28		Тело массой m соединенное с вертикальной пружиной жесткостью с. В начальный момент тело вывели из положения равновесия на величину l и сообщили скорость v₀, направленную вниз. Получить уравнение движения тела, если на него действует сила сопротивления среды .
29		Тело массой 4 кг лежит на невесомой балке в равновесии. Сила упругости балки пропорциональна ее прогибу и равна F = 6x (Н). Телу сообщают скорость 2 м/с, направленную вниз. Получить уравнение дальнейшего движения груза, если сопротивление движению R = 20v (H, м/с).
30		На вертикально расположенной пружине подвешен груз массой 15 кг, в результате чего пружина получила статическое удлинение 2 см. Грузу сообщают направленную вниз скорость 5 м/с, и он начинает колебаться. Найти жесткость пружины и уравнение движения груза.

Пример выполнения задания

Рис. 7

Тело массой 2 кг висит в равновесии на пружине жесткости 8 Н/см. Телу сообщают скорость 20 см/с, и оно начинает колебаться в среде, сопротивление которой пропорционально скорости тела. Амплитуда после четырех колебаний уменьшилась в 12 раз. Определить уравнение движения тела и период его колебаний.

Решение:

Изобразим тело в произвольном положении согласно схеме. Совместим начало координат О с положением статического равновесия груза, направив ось по направлению движения груза. Изобразим действующие силы . Составим дифференциальное уравнение движения.