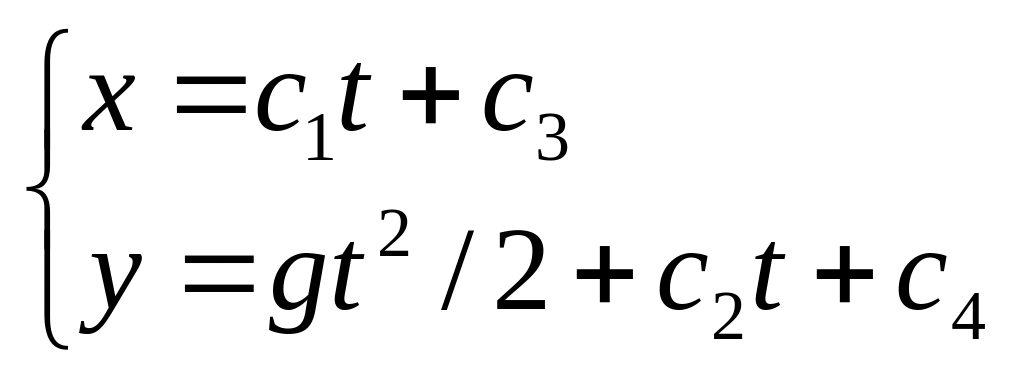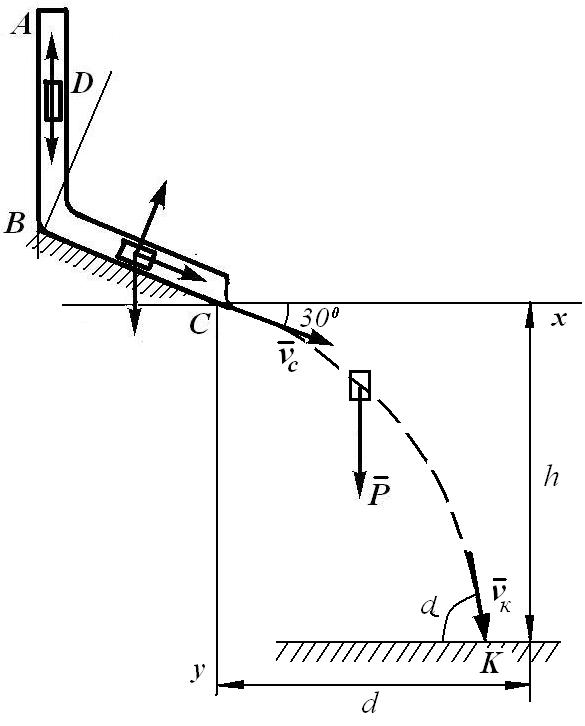
1.4. Криволинейное движение точки

Задание. Тело D, покидает участок трубы ВС со скоростью . Эта скорость найдена в предыдущем задании. В вариантах 13, 19, 21, 22, 23, 24 и 26 отклонить начальную скорость на 60⁰ от вертикали.

Таблица 1.2

Номер вар. d h t* 1 10 - - 2 - 6 - 3 - - 2 4 - 4 - 5 5 - - 6 - - 3 7 - 5 - 8 - - 10 9 - 7 - 10 10 - - 11 - 3 - 12 - 5 - 13 10 - - 14 - - 2 15 15 - -

Номер вар. d h t* 16 10 10 - 17 2 2 - 18 3 3 - 19 - - 3 20 - 4 - 21 - - 2 22 20 - - 23 10 - - 24 - - 3 25 20 - - 26 20 - - 27 - 5 - 28 - - 4 29 15 - - 30 - 2 -

За t^* сек тело движется в пространстве под действием только силы тяжести (сопротивлением воздуха пренебречь) и попадает в точку К со скоростью .

Точка К находится на расстоянии d по горизонтали от точки С и на расстоянии h по вертикали от нее.

Используя схемы рисунков 1–3 и взяв скорость как начальную для участка СК, определить значение и направление скорости , с которой тело D попадет в точку К. Также найти неизвестные величины (d, h или t^*), указанные в таблице 1.2 прочерком.

Пример выполнения задания:

Рис. 5	, m= 2 кг Изображаем тело d на участке СК в произвольном положении (рис. 5) с одной приложенной к нему силой тяжести. Вводим систему координат ХУ с началом в точке С. Записываем дифференциальное уравнение движения тела D в проекциях на координатные оси
		(2.1)
	или	(2.2)

Разделяя переменные в (2.2), сокращая на m и интегрируя, получим закон изменения скорости

.

(2.3)

Интегрируя (2.3), получим закон движения груза D в координатной форме

(2.4)

Постоянные интегрирования определяем из начальных условий задачи:

при

(2.5)

Подставляя начальные условия (2.5) в уравнения (2.3) и (2.4) находим из (2.3) , а из (2.4) .

Окончательно уравнения изменения скорости

(2.6)

Уравнения движения груза D на участке СК

(2.7)

Зная высоту падения груза h = 5 м и используя второе уравнение в (2.7) найдем время движения груза от точки С до точки К.

Принимая здесь получим

или , откуда

.

Так как время может принимать только положительное значение, то . Тогда расстояние, пройденное грузом по оси х за это время из (2.7) будет

.

Скорость тела D при падении найдем через проекции скорости на оси координат из (2.6)

.

Для момента падения в точку К

Направление скорости , т.е под каким углом, например, к горизонтальной оси этот вектор направлен, найдем

.