1.2. Последовательность составления и решения дифференциальных уравнений

При решении второй задачи динамики точки рекомендуется придерживаться следующего плана:

1. Изобразить материальную точку в произвольном положении в выбранной системе координат.

2. Изобразить на рисунке все силы, действующие на точку (активные и реакции связей).

3. Записать II закон Ньютона, т. е. уравнение (1), в векторной форме.

4. Спроецировать полученное уравнение на координатные оси в форме (4).

5. Сформулировать начальные условия движения точки (3).

6. Проинтегрировать дифференциальные уравнения (4), определяя постоянные интегрирования по начальным условиям.

7. Из полученных зависимостей найти искомые величины.

Примечание: рекомендуется все решение проводить до конца в общем виде (в буквах), подставляя численные данные только в окончательные результаты.

1.3. Прямолинейное движение точки

Задание. Груз D массой m, получив в точке A начальную скорость движется в изогнутой трубе АВС (рисунки 1–3). На участке АВ кроме силы тяжести на него действует постоянная сила (ее направление показано на рисунках) и сила сопротивления среды , зависящая от скорости груза (направлена против движения), значение которой задано в таблице 1.1. В точке В груз не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила , проекция которой на ось х задана в таблице 1.1.

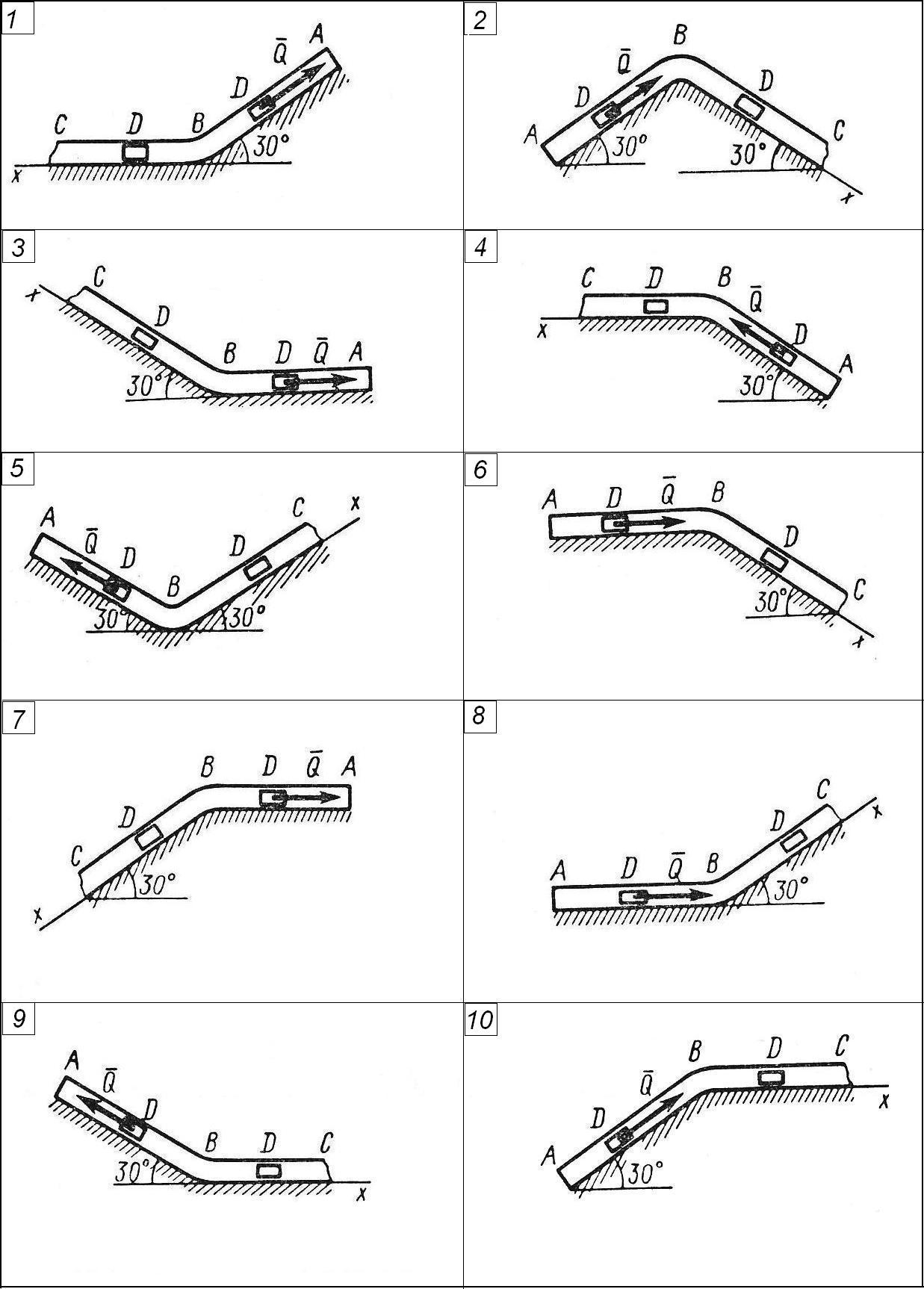
Рис. 1

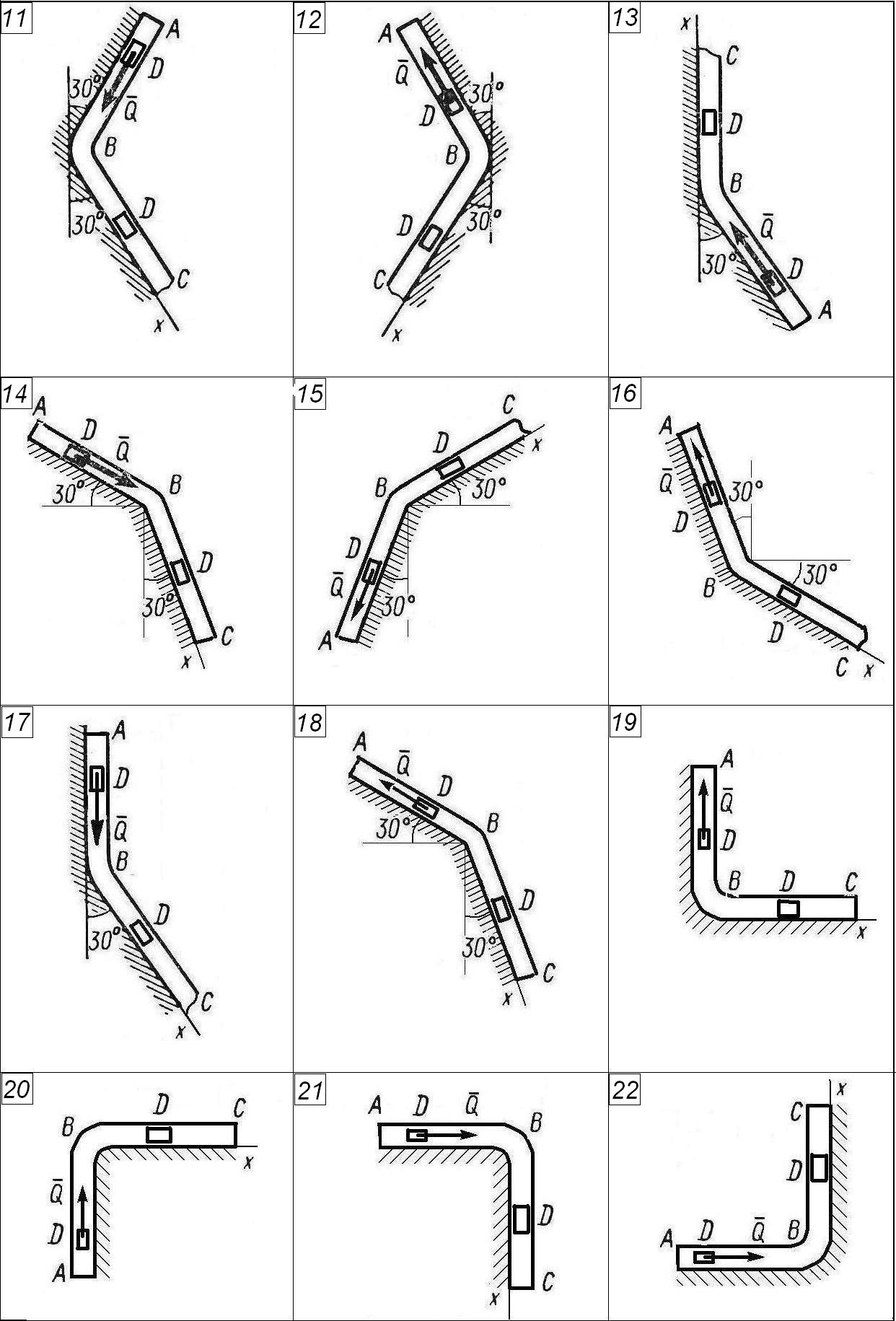Рис. 2

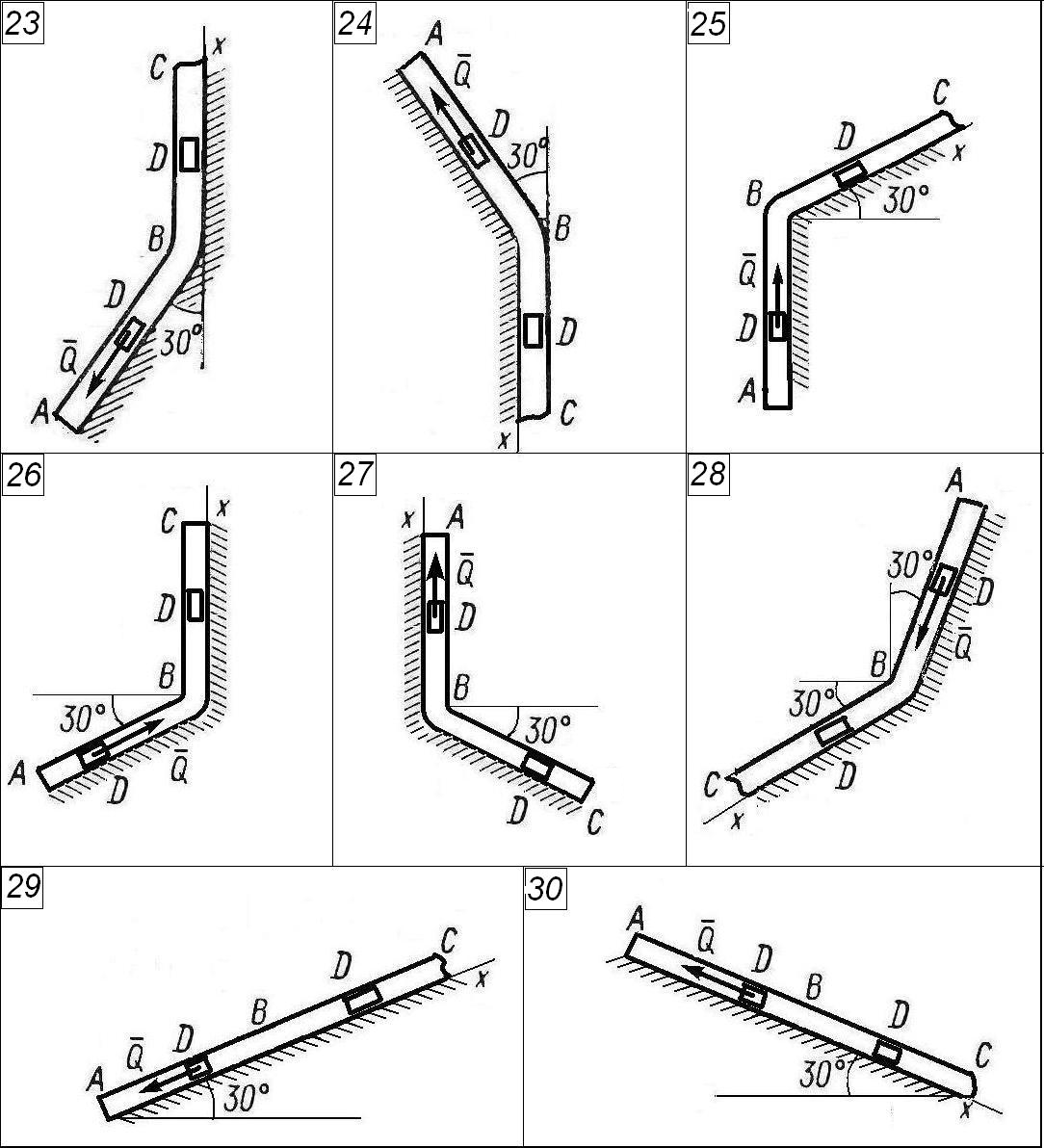
Рис. 3

Считая груз материальной точкой и зная расстояние АВ = l или время движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. x = f(t), где х = ВD и длину участка ВС, считая, что эту часть трубы тело D проходит за 1 сек. Определить скорость груза D в точке С. Трением груза о трубу пренебречь.

Указания. Эта задача решается интегрированием дифференциальных уравнений движения точки. Сначала нужно составить и проинтегрировать методом разделения дифференциальное уравнение точки (груза) на участке АВ, учтя начальные условия. Затем зная время движения на участке АВ или его длину, определить, какую скорость будет иметь груз в точке В. Эта скорость будет начальной для движения груза на участке ВС.

Таблица 1.1

Номер условия	m, кг		Q, Н	R, Н	l, м	t1, с	Fx, Н
1	2.4	12	5	0.8v2	1.5	-	4sin(4t)
2	2	20	6	0.4v	-	2.5	-5cos(4t)
3	8	10	16	0.5v2	4	-	6t2
4	1.8	24	5	0.3 v	-	2	-2cos(2t)
5	6	15	12	0.6 v2	5	-	-5sin(2t)
6	4.5	22	9	0.5 v	-	3	3t
7	4	12	10	0.8 v2	2.5	-	6cos(4t)
8	1.6	18	4	0.4 v	-	2	-3sin(4t)
9	4.8	10	10	0.2 v2	4	-	4cos(2t)
10	3	22	9	0.5 v	-	3	4sin(2t)
11	1.5	11	3	0.5 v2	1.5	-	3sin(t)
12	2	21	10	0.4 v	-	5	-2cos(t)
13	1.2	12	5	0.6 v2	2	-	4t2
14	4	20	6	0.4v	-	5	-4sin(4t)
15	2	15	16	0.4v2	2.5	-	6cos(3t)
16	3.2	24	5	0.8v	-	4	3t
17	6	15	12	0.3 v2	5	-	-3sin(4t)
18	1.5	22	9	0.5 v	-	3	-2cos(4t)
19	2.1	12	10	0.7 v2	3	-	2sin(2t)
20	3	18	20	0.6 v	-	2.5	5cos(4t)
21	2.4	10	10	0.4 v2	1.5	-	-6sin(3t)
22	1.6	22	9	0.2 v	-	4	-4cos(2t)
23	4	11	3	0.8 v2	2.5	-	2sin(4t)
24	2.4	21	5	0.6 v	-	4	-3cos(3t)
25	4	11	12	0.5 v2	2	-	4t2
26	6	20	15	0.6 v	-	5	3sin(3t)
27	1.4	10	4	0.7 v2	3	-	2cos(2t)
28	1.5	10	9	0.5 v	-	3	5t
29	1.8	24	14	0.6 v2	1.5	-	3sin(4t)
30	2.4	15	5	0.2 v	-	6	-6cos(2t)

Пример выполнения задания. На вертикальном отрезке трубы АВС (рис. 4) на груз D массой m= 2 кг действует сила тяжести и сила сопротивления , где ; расстояние АВ = l = 2,5 м, скорость в точке А . На наклонном участке на груз действует сила тяжести и переменная сила . Определить закон движения x = f(t) на участке ВС, длину этого участка, учитывая, что тело проходит его за 1 сек, а также скорость в точке С.

Рис. 4

1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз в произвольном положении и действующие на него силы и . Проводим ось Az и записываем уравнение (1) в проекции на эту ось. или, учитывая что , .

Или

.

(1.1)

Введем для сокращений записей обозначения: , .

.

(1.2)

Интегрируя обе части (1.2) получим

.

(1.3)

По начальным условиям , и выражению (1.3) находим, что

.

Подставляя в (1.3) и приводя подобные, находим

.

Применяя логарифмические тождества, получим

или, подставляя n и k,

и принимая значения е = 2.7 и z = l, получим

, т. е. скорость в точке В будет

.

(1.4)

2. Теперь рассмотрим движение груза на участке ВС. Найденная скорость будет на этом участке начальной. Изображаем груз в произвольном положении и действующие на него силы тяжести , нормальной реакции опоры и переменной силы .

Проведем из точки В ось Вх и составим дифференциальное уравнение (1) движения груза в проекции на эту ось:

.

(1.5)

Так как , , , то уравнение (1.5) примет вид

.

(1.6)

Разделив обе части уравнения (1.6) на m = 2 кг и полагая ,

.

умножая обе части на dt и интегрируя, получим

.

(1.7)

Постоянную интегрирования найдем из начальных условий. В момент времени t=0 на участке ВС , откуда

Итак, скорость на участке ВС будет изменяться по закону

.

(1.8)

Скорость в конце участка ВС, т. е. через 1 сек. будет равна

умножая в (1.8) обе части на dt и снова интегрируя, найдем

Так как при t = 0, х = 0, то и окончательно искомый закон движения груза будет

(м)

(1.9)

А длина участка ВС при t = 1сек

Ответ: ,

,

.