- •И.Ю. Гордлеева, т.И. Тарнопольская Теоретическая механика
- •Введение
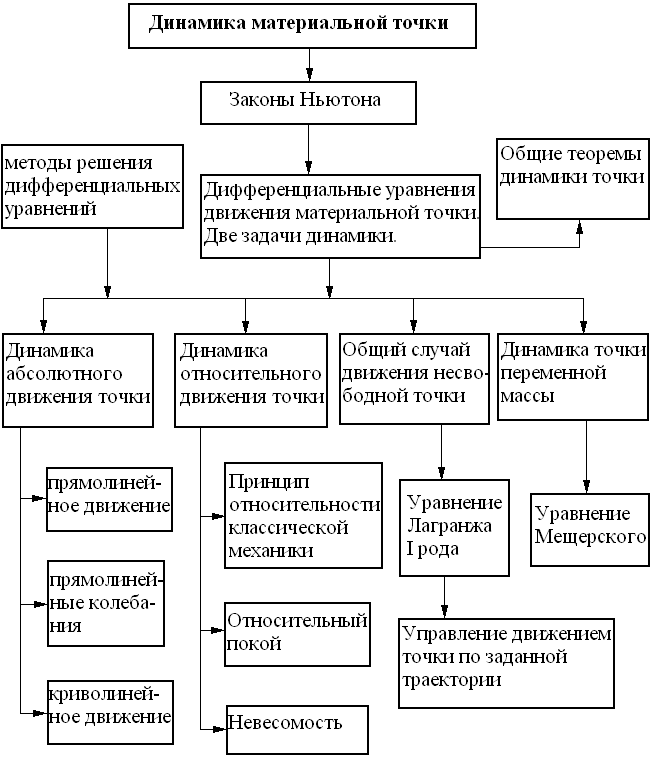
- •Глава 1. Динамика абсолютного движения материальной точки
- •1.1. Дифференциальные уравнения движения точки
- •1.2. Последовательность составления и решения дифференциальных уравнений
- •1.3. Прямолинейное движение точки
- •1.4. Криволинейное движение точки
- •Вопросы для самоконтроля.
- •1.5. Прямолинейные колебания точки
- •Обобщенные жесткости пружин
- •Глава 2. Динамика относительного движения материальной точки
- •2.1. Основные теоретические сведения
- •2.2. Последовательность составления и решения уравнений
- •Литература
- •Оглавление
- •Гордлеева Ирина Юрьевна,
- •Тарнопольская Татьяна Ивановна
- •Теоретическая механика
- •Дифференциальные уравнения
- •Движения материальной точки
Федеральное агентство морского и речного транспорта
Федеральное государственное образовательное учреждение
высшего профессионального образования
Волжская государственная академия водного транспорта
Кафедра прикладной механики
и подъемно-транспортных машин
И.Ю. Гордлеева, т.И. Тарнопольская Теоретическая механика
Дифференциальные уравнения
движения материальной точки
Методические указания и индивидуальные задания
для самостоятельной работы студентов
очного и заочного факультетов инженерных специальностей
Нижний Новгород
Издательство ФГОУ ВПО «ВГАВТ»
2006
УДК 531.8
Г68
Гордлеева, И.Ю.
Теоретическая механика. Дифференциальные уравнения движения материальной точки: методические указания и индивидуальные задания для самостоятельной работы студентов очного и заочного факультетов инженерных специальностей / И.Ю. Гордлеева, Т.И. Тарнопольская. – Н. Новгород: Изд-во ФГОУ ВПО «ВГАВТ», 2006. – 35 с.
Кратко изложены основные виды движения материальной точки (прямолинейное, криволинейное, колебательное и относительное движения). Приведена последовательность составления и интегрирования дифференциальных уравнений движения материальной точки. По каждой теме приведены примеры решения задач и индивидуальные задания для самостоятельной работы студентов. Задания составлены на основе сборников заданий по теоретической механике А.А. Яблонского, С.М. Тарга и И.В. Мещерского.
Рекомендованы к изданию кафедрой прикладной механики и подъемно-транспортных машин, протокол № 10 от 28 июня 2006 г.
© ФГОУ ВПО «ВГАВТ», 2006
Введение
Динамика – раздел теоретической механики, в котором изучается движение материальных тел с учетом действующих сил, вызывающих это движение.
|
При создании нового инженерного объекта на этапе его проектирования широко используются физические и математические модели механических процессов.
Основой математических моделей являются уравнения движения тел под действием сил. Динамика дает базовые знания по составлению этих уравнений.
В динамике обычно выделяют подраздел «динамика материальной точки». Материальная точка (абстракция) – тело, имеющее массу и размерами которого можно пренебречь.
Схематизация точкой возможна, например, при рассмотрении его поступательного движения, при малых относительных размерах тела, при частичном или качественном анализе движения.
Методы динамики точки позволяют получить практически значимые результаты при изучении движения самых различных объектов: кораблей, поездов, механизмов и др.
Глава 1. Динамика абсолютного движения материальной точки
1.1. Дифференциальные уравнения движения точки
Основное дифференциальное уравнение динамики точки в общем случае имеет вид
|
(1) |
и по сути выражает второй закон Ньютона
|
(2) |
где![]() – масса точки,
– масса точки,
![]() –
радиус-вектор,
описывающий траекторию точки относительно
неподвижного центра,
–
радиус-вектор,
описывающий траекторию точки относительно
неподвижного центра,
![]() – сумма активных
сил и сил реакции связей. При этом каждая
сила
– сумма активных
сил и сил реакции связей. При этом каждая
сила
![]() может быть
может быть
– постоянной:
![]() ;
;
– функцией времени
![]() :
:
![]() ;
;
– функцией
координаты
![]() :
:
![]() ;
;
– функцией скорости
![]() :
:
![]() ;
;
– в общем случае
зависеть от всех параметров:
![]() .
.
Выражение (1) называется дифференциальным уравнением точки в векторной форме. Общее решение дифференциального уравнения (1) содержит произвольные постоянные, определяемые по начальным условиям.
Начальные условия
движения – это положение и скорость
точки при
![]() :
:
![]() ,
,![]() .
.
В системе декартовых координат1 начальные условия движения имеют вид:
при
:
|
(3) |
В соответствии с (1) в динамике точки можно поставить и решить две основные задачи динамики точки:
Первая (прямая) задача – это нахождение сил, действующих на точку, если известны масса точки и закон ее движения.
Вторая (обратная) задача – это нахождение закона движения точки, если известны масса точки, действующие на нее силы и начальные условия движения.
Обе задачи можно решить с помощью дифференциальных уравнений, получающихся проецированием уравнения (1) или (2) на координатные оси:
|
(4) |