13. Основные понятия систем управления и автоматизации. Постановка задачи управления и регулирования.
Одной из самых главных особенностей современной научной и технической деятельности является подход к объектам исследования и проектирования как к системам
Система ‑ это не сумма составляющих ее частей, целостное образование с новыми свойствами, которыми не обладают ее элементы.
Моделью системы называют отображение определенных характеристик объекта с целью его изучения. Поэтому центральной проблемой моделирования является разумное упрощение модели, т.е. выбор степени подобия модели и объекта.
Любой целенаправленный процесс представляет собой организованную совокупность операций, которые условно можно разделить на две группы: рабочие операции и операции управления.
Рабочие операции ‑ это действия, необходимые непосредственно для выполнения процесса в соответствии с природой и законами, определяющими ход течения процесса.
Для достижения цели процесса рабочие операции должны организовываться и направляться действиями другого рода ‑ операциями управления. Совокупность операций управления образуют процесс управления. В структурном аспекте любую систему управления можно представить взаимосвязанной совокупностью объекта управления и управляющего органа
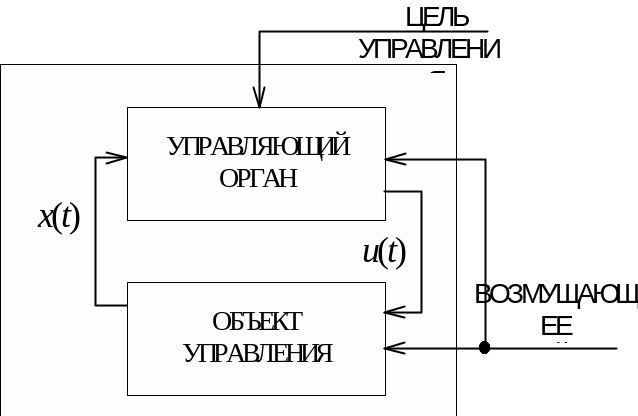
Обобщенная структура системы управления
Задачу управления можно сформулировать следующим образом: найти такие вектор управления и вектор состояния, которые обеспечат достижение цели управления, согласно какого-то критерия управления.
;
В некоторых случаях задачу управления
можно сформулировать следующим образом:
найти и реализовать функциональную
зависимость (алгоритм управления)
,обеспечивающих
наилучшее приближение к заданному
значению критерия управления.
Это частный случаем задачи называется
задачей регулирования. Строго задача
регулирования формулируется следующим
образом: полагая заданным х*(t),
найти закон регулирования
,который
обеспечивает экстремум критерию (1)
Процесс управления условно можно разбить на совокупность следующих функций:
‑ планирование и определение программы управления;
‑ контроль;
‑ формирование управляющих воздействий или принятия решения;
‑ реализаци управляющего воздействия или решения.
Определение программы управления (планирования) заключается в выработке траектории решения системы х*(t) в пространстве параметров его состояния.
Контроль состоит в измерении значений компонентов вектора состояния х(t) и определении вектора ошибки (t).
Формирование управляющего воздействия (принятия решения) заключается в определении значений управляемых переменных, приводящих объект управления в желаемое состояние.
Реализация управляющих воздействий ‑ это непосредственно физическое воздействие на объект управления.
Функциональная схема системы управления
Схема системы регулирования
16. Применение позиционного регулирования пид-регуляторов. Способы технической реализации систем регулирования
ПИД – регулятор вырабатывает выходной сигнал равный сумме трех составляющих П(пропорционального регулирования) + И(регулирование по интегралу) + Д(регулирование по производной). Уравнение классического ПИД-регулятора:
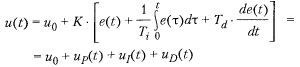
up(t) – разность между выходной величиной опорным значением, uI(t) – интеграл по времени ошибки выходной величины, uD(t) – производная ошибки. К – коэффициент усиления регулятора, Ti – постоянная времени интегрирования, Td – постоянная времени дифференцирования, u0 – поправочное значение (или смещение), настраивающий средний уровень выходного сигнала регулятора. Параметры К, Ti, Td – можно настроить с помощью ручек на панели управления регулятора. К – может быть безразмерным (но иногда в технических единицах; например, расход – м3 *с-1).
Т.к. ПИД-регулятор представляет систему второго порядка, то его можно применять для управления процессами с динамикой второго порядка.
В некоторых системах управления процессами опорное значение время от времени резко изменяется, а между скачками остается постоянным. Скачек опорного значения приводит к резкому изменению выходного сигнала регулятора, этот эффект «всплеском производной».
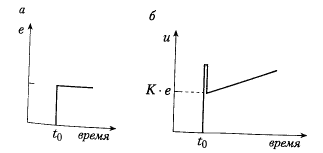
Переходная характеристика ПИД – регулятора: а - скачок ошибки происходит в момент t0; б -дифференциальная часть регулятора – причина всплеска в величине выходного сигнала;
Существует два типа алгоритма регулятора – позиционный и приращений.
В позиционном алгоритме выходной сигнал представляет собой абсолютное значение управляющей переменной исполнительного механизма. Дискретный ПИД – регулятор имеет вид:
Интеграл аппроксимируется конечными разностями:
с постоянной
.
Величина второго слогаемого при малых
h и больших Ti
может стать очень мальнькой, поэтому
нужно позаботиться о том, чтобы обеспечить
необходимую точность его машинного
представления.
Дифференциальная часть ПИД-регулятора:
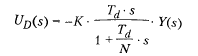
Если постоянная времени дифференциального члена Td = 0, следовательно дифференцирование описывается простой разностной аппроксимацией выходного сигнала dy/dt.
Системы двухпозиционного регулирования
Они имеют в своем составе двухпозиционный или Пз-регулятор, выходная величина которого может принимать только два значения, максимальной хmax и минимальной xmin величинам регулирующего воздействия. Такие системы относятся к нелинейным. Структурная схема:
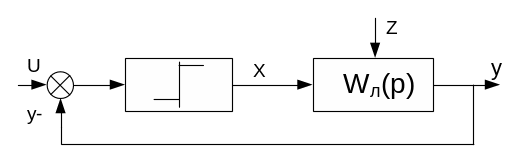
Для работоспособности системы
двухпозиционного регулирования нужно,
чтобы при равенстве передаточных функций
Wx(p) и Wz(p)
по каналам
и
текущие значения эквивалентного
возмущения объекта zэкв.
лежали бы в пределах
.
Это условие соответствует случаю, когда
основным возмущением z
является нагрузка объекта, изменение
которой компенсируется регулирующим
воздействием.
Пз-регулятор вырабатывает регулирующее воздействие, равное xmax, если текущее значение регулируемой величины у ниже ее заданного значения u, в этом случае регулируемая величина возрастает. При достижении текущим значением заданного, регулирующее воздействие х мгновенно уменьшается до хmin. Но т.к. у объект обладает инерционностью, то регулируемая величина еще продолжает возрастать в течении некоторого времени и затем понижается. При последующем пересечении регулируемой величиной заданного значения регулятор снова сформирует регулирующее воздействие xmax, что через некоторое время вновь перейдет к очередному повышению регулируемой величины. Следовательно при использовании Пз-регулятора регулируемая величина совершает колебания относительно заданного значения. Эти колебания с амплитудой А и периодом колебания T - автоколебания.
ПИД-регуляторы успешно применяются для решения многих задач управления промышленными процессами. Основная причина их широкого распространения связана с тем, что динамические свойства большинства технических процессов можно удовлетворительно аппроксиморовать динамическими моделями второго порядка. Но ПИД – регулятор не подходит для управления процессами в которых значительную роль играют следующие факторы: 1) временные задержки, 2) колебательных характер динамики системы, 3) изменения параметров, как предсказуемые, так и не предсказуемые.