Ответы к экзамену по дисциплине Математика (теория)
Определения множества и основных операций над множествами.
Множество – совокупность объектов, собранных по определенному признаку.
Объединением множеств называют новое множество, состоящее из элементов, принадлежащих хотя бы одному из множеств – слагаемых.
Пересечением множеств называют новое множество, состоящее из элементов, одновременно принадлежащих данным множествам.
Разностью двух множеств называют новое множество, состоящее из элементов первого множества, не входящих во второе множество.
Модуль действительного числа. Основные свойства модуля.
Модулем действительного числа называется само это число, если оно не отрицательно, и число ему противоположное, если оно отрицательно.
Свойства модулей:
;
;
;
;
;
=>
;=>
;
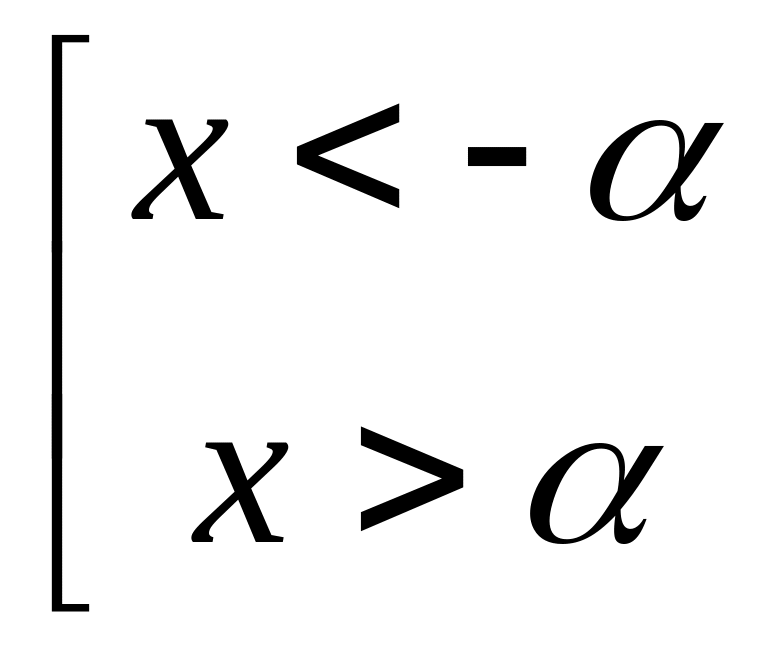- модуль разности,
это расстояние между числами.
Определение мнимой единицы. Определение комплексного числа, его изображение.
Число, квадрат равен -1, называется мнимой единицей и обозначается буквой i.
Число
вида a+b
i,
где a
и
b
действительные числа, а i
мнимая
единица, называется комплексным,
кратко обозначающиеся z.
Комплексные числа изображаются в виде точки в координатной плоскости:
Действительная часть;
Коэффициент мнимой части.
Сопряженные числа симметричны оси абсцисс.
Три формы записи комплексного числа. Переход от алгебраической формы к тригонометрической.
3 формы записи комплексного числа:
Алгебраическая форма;
Тригонометрическая форма;
Экспоненциальная (показательная) форма.
Для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
Действия с комплексными числами в алгебраической форме.
Сложение: Сумма двух комплексных чисел
и
будет комплексное число вида
;Вычитание: Разность двух комплексных чисел и будет комплексное число вида
;Умножение: Произведение двух комплексных чисел и будет комплексное число вида
;Деление: Частное двух комплексных чисел и будет комплексное число вида z =
=
;
Действия с комплексными числами в тригонометрической форме.
Умножение
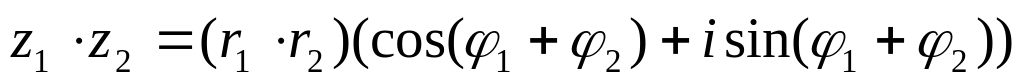при
умножении комплексных чисел в
тригонометрической форме модули
умножаются, а аргументы складываются.Деление
при
делении комплексных чисел в
тригонометрической форме модули
делятся, а аргументы вычитаются.Возведение в степень
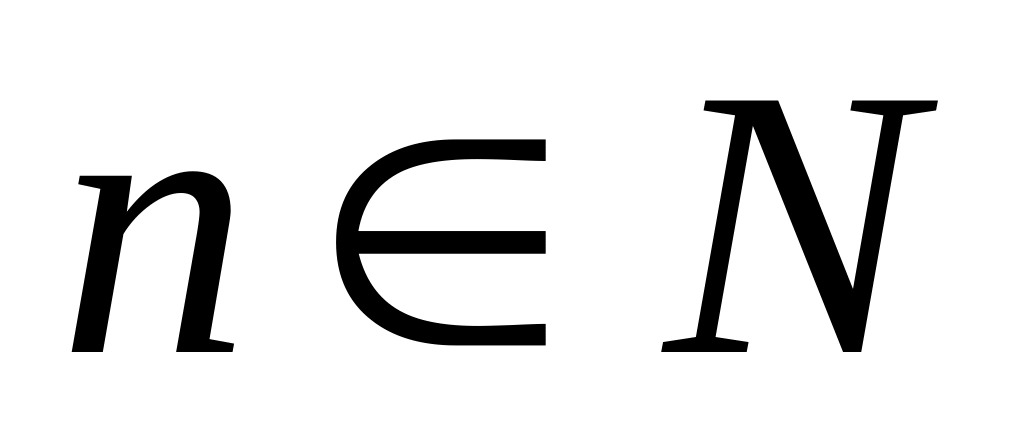при
возведении комплексных чисел в
тригонометрической форме в степень,
модуль возводится в степень, а аргументы
умножаются на показатель степени.Извлечение корня
,
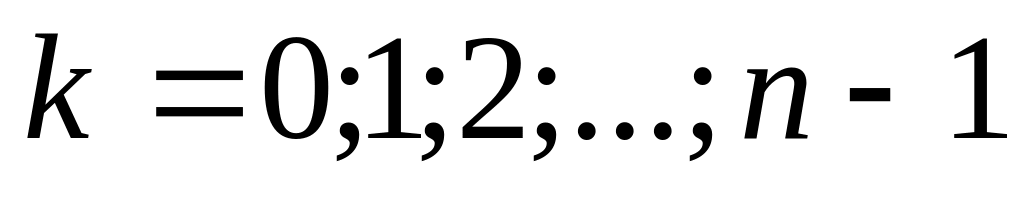.Формула Муавра
.
Функция: определение и обозначение. Способы задания функции.
Функцией
на множествах
и
называется
закон, по которому каждому элементу
множества
соответствует единственный элемент
множества
.
Обозначение:
Способы задания:
Аналитический – функция выражается формулой;
Графический – задание функций в виде множества точек в координатной плоскости;
Табличный – это задание конечного числа пар значений аргумента и значений функций;
Словесный – зависимость между переменными задается в виде текста.
Четность и нечетность функции.
Функция
называется четной,
если для любого значения
,
взятого из области определения функции,
значение
также принадлежит области определения
и выполняется равенство
;
Функция
называется нечетной,
если для любого значения
,
взятого из области определения функции,
значение
также принадлежит области определения
и выполняется равенство
.
Монотонность функции
Монотонность – это возрастание или убывание функции;
Функция
,
заданная на множестве
называется возрастающей,
если большему значению аргумента
соответствует большее значение функции;
Функция , заданная на множестве называется убывающей, если меньшему значению аргумента соответствует меньшее значение функции;
Числовая последовательность. Определение предела числовой последовательности.
,
-числовая
последовательность;
Функция, заданная на множестве натуральных чисел называется числовой последовательностью.
Число
называется пределом
числовой последовательности
,
если для любого положительного числа
Эпсилон найдется такое натуральное
число N,
что для всех элементов последовательности
с номерами большими этого числа будет
выполняться неравенство
.
11. Бесконечно малые величины, их свойства.
Бесконечно малые обозначаются греческим алфавитом.
;
,
Произведение бесконечно малой последовательности и ограниченной последовательности называется бесконечно малой;
Для сходящейся последовательности её элементы представлены в виде суммы предела и бесконечно малой последовательности.
12. Определение предела функции в точке.
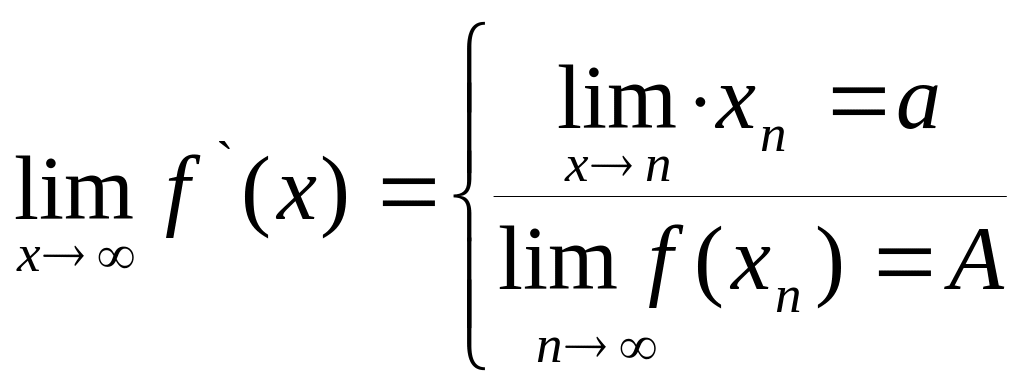
Число
называется пределом функции
в точке
,
если для любой последовательности
значений её аргумента, сходящейся в
предельной точке
,
соответствующая последовательность
значений функции сходится к
.
Определение непрерывности функции в данной точке.
Функция называется непрерывной, если:
Она определена в этой точке;
Имеет предел в этой точке, равный значению функции в предельной точке.