Тема 9. Информационное обеспечение анализа хозяйственной деятельности.
Экономическая информация. Носители информации. Виды информации, используемой в АХД. Планово-нормативная информация. Отчетно-учетная информация. Внеучетные источники информации. Требования к качеству информационного обеспечения. Полнота, достоверность, своевременность и возможности использования информации в АХД. Ценность экономической информации: потребительская, экономическая, эстетическая. Методика накопления и систематизации аналитических данных. Требования, предъявляемые к организации сбора, накопления и систематизации информации. Основа своевременного получения информации. Достоверность экономической информации и методы ее повышения. Достоверность планово-нормативных данных. Достоверность отчетных материалов.
Тема 10. Организация экономического анализа.
Система органов анализа и контроля. Внешний экономический анализ предприятия. Внутренний экономический анализ предприятия. Схема распределения функций экономического анализа. Основные этапы экономического анализа:
Составление программы экономического анализа;
Отбор и проверка информации;
Выбор и расчет показателей;
Аналитическая обработка и сравнение показателей;
Обобщение результатов, гласность анализа и контроль за реализацией его результатов. Стратегия определения главных целей деятельности предприятия и возможность их достижения.
Тема 11. Информационные технологии экономического анализа(итэа)
Содержание и организация экономического анализа в условиях АСУП. Понятие математического, технического, информационного, методического и организационного обеспечения. Использование табличных процессоров и баз данных в экономическом анализе (на примере EXCEL) Специальные пакеты прикладных программ. Перспективы развития ИТЭА в Украине.
Тема 12. Законы распределения дискретной случайной величины. Закон нормального распределения непрерывной случайной величины.
Принятие решения в условиях недостатка информации. Распределение дискретной случайной величины (биноминальное распределение и закон распределения Пуассона). Нормальное распределение непрерывной случайной величины.
Тема 13. Маржинальный анализ.
Аналитическая оценка решения о принятии дополнительного заказа по цене ниже себестоимости продукции. Обоснование структуры товарной продукции. Обоснование варианта цены на новое изделие. Выбор вариантов машин и оборудования. Обоснование решения “ производить или покупать ”. Выбор варианта технологии производства. Выбор решения с учетом ограничения на ресурсы. Обоснование эффективности инвестиционных проектов.
Задание для заочников включает 5 задач :
Задание 1.
Используя традиционные приемы и методы экономического анализа (не менее 3) на основе эмпирического материала, полученного на предприятии провести анализ экономических процессов и явлений. Используемые традиционные приемы и методы :
сравнение
группировка
детализация и обобщение
прием выделения “узких мест” и “ведущих звеньев”
прием цепных подстановок
прием пропорционального деления
интегральный метод
индексный метод.
Задание 2.
Используя метод корреляционно-регрессионного анализа оценить взаимосвязь фактора и результирующего показателя, выбрать адекватную модель прогноза.
пример
Построить экономико-математическую модель платежеспособного спроса на продукты питания от уровня доходов семьи по данным проведенного опроса 8 групп семей (числа относительные в расчете на 100 грн. дохода и расхода).
Таблица 1.
Доходы семьи |
1,4 |
3,3 |
5,5 |
7,6 |
9,8 |
12,0 |
14,7 |
18,9 |
Расходы на продукты питания |
1,1 |
1,4 |
2,0 |
2,4 |
2,8 |
3,1 |
3,5 |
4,0 |
Оценим корреляционную связь между фактором и признаком по формуле
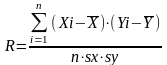(1)
R=0.999
Коэффициент корреляции указывает на весьма тесную связь между доходами и расходами семьи на продукты питания.
Построим график зависимости
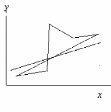
Рис. 1. График зависимости платежеспособного спроса на продукты питания от уровня доходов семьи.
Из графика определяем, что более всего подходит линейная зависимость вида: y=a+bx. Значения коэффициентов a, b определяем из системы нормальных уравнений :
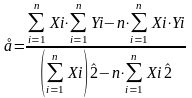
(2)
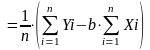
Для удобства расчетов результаты вычислений запишем в таблицу 2.
Таблица 2
№ п/п |
xi |
yi |
xi2 |
yi2 |
xiyi |
|
|
( |
|
(yi
-
|
1 |
1,4 |
1,1 |
1,96 |
1,21 |
1,5 |
1,21 |
-0,11 |
0,012 |
-1,44 |
2,073 |
2 |
3,3 |
1,4 |
10,89 |
1,96 |
4,6 |
1,52 |
-0,12 |
0,014 |
-1,14 |
1,293 |
3 |
5,5 |
2,0 |
30,25 |
4,0 |
11,0 |
1,87 |
0,13 |
0,017 |
-0,54 |
0,288 |
4 |
7,6 |
2,4 |
57,76 |
5,8 |
18,2 |
2,20 |
0,20 |
0,040 |
-0,14 |
0,019 |
5 |
9,8 |
2,8 |
96,04 |
7,8 |
27,4 |
2,56 |
0,24 |
0,058 |
0,26 |
0,068 |
6 |
12,0 |
3,1 |
144,0 |
9,6 |
37,2 |
2,91 |
0,19 |
0,036 |
0,56 |
0,316 |
7 |
14,7 |
3,5 |
216,1 |
12,3 |
51,4 |
3,34 |
0,16 |
0,026 |
0,96 |
0,926 |
8 |
18,9 |
4,0 |
357,2 |
16,0 |
76,5 |
4,01 |
0,01 |
0,001 |
1,46 |
2,139 |
Сумма |
73,2 |
20,3 |
914,2 |
58,7 |
227,1 |
|
|
0,204 |
|
7,125 |
Среднее арифметическое |
9,15 |
2,53 |
|
|
28,38 |
|
|
|
|
|
)2
)2
Получим систему нормальных уравнений
8a
+ 73,2b = 20,3
73,2a + 914,2b = 227,1
Решив ее, получим a = 0,99; b = 0,16.
Экономико-математическая модель спроса на продукты питания в зависимости от уровня дохода семей имеет вид:
=
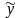0,99 + 0,16 x
Рассчитаем теоретические значения спроса по формуле:
=
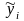0,99 + 0,16 x
и нанесем их на график. Получим теоретическую линию уравнения регрессии.
Оценим степень достоверности прогноза расчета экономического показателя по найденному теоретическому уравнению регрессии
=
=
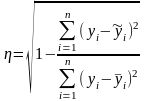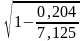0,98
Найдем ошибку уравнения регрессии
=
=
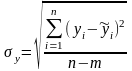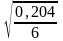0,8
По найденному уравнению регрессии осуществим прогноз для трех заданных значений фактора :
х = 0.99 + 0.16 20.2 = 4.22
х = 0.99 + 0.16 22.4 = 4.57
х = 0.99 + 0.16 26.5 = 5.23
Задание 3.
Используя симплекс метод линейного программирования разработать оптимальный план.
пример
Для изготовления различных изделий А, В, С предприятие использует 3 различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена 1 изделия А, В, С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице 3
Таблица 3
Вид сырья |
Нормы затрат сырья (кг) на 1 изд. |
Общее кол-во сырья (кг) |
|
А В С |
|
1 |
18 15 12 |
360 |
2 |
6 4 8 |
192 |
3 |
5 3 3 |
180 |
Цена 1 изд.(грн.) |
9 10 16 |
|
Составим математическую модель задачи. Искомый выпуск изделий А обозначим черезх1, В - х2, С - х3. Поскольку переменные х1, х2, х3 должны удовлетворять следующие
системы неравенств :
18х1+15х2+12х3<=360
6х1+4х2+8х3<=192 (3)
5х1+3х2+3х3<=180
Общая стоимость произведенной предприятие продукции при условии выпуска х1
изделий А, х2 изделий В, х3 изделий С составляет F=9х1+10х2+16х3 (4)
По своему экономическому содержанию х1, х2, х3 могут принимать только лишь не отрицательные значения : х1,х2,х3>=0
Таким образом приходим к следующей математической задаче : среди всех
неотрицательных решений системы неравенств (3) требуется найти такое, при котором функция (4) принимает максимальное значение. Запишем эту задачу в форме основной задачи ЛП. Для этого перейдем от ограничений - неравенств к ограничениям - равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений :
18х1+15х2+12х3+у1=360
6х1+4х2+8х3+у2=192 (5)
5х1+3х2+3х3+у3=180
F=-9(-х1)-10(-х2)-16(-х3)
Эти дополнительные переменные у1,у2,у3 по экономическому смыслу означают неиспользуемое при данном плане производства количество сырья того или иного вида. Параметр у1 - это неиспользуемое количество сырья 1 вида. Составим исходную симплекс таблицу :
Таблица 4.
|
-х1 |
-х2 |
-x3 |
свободный член |
у1 |
18 |
15 |
12 |
360 |
y2 |
6 |
4 |
8 |
192 |
у3 |
5 |
3 |
3 |
180 |
F |
-9 |
-10 |
-16 |
|
Этот план не является оптимальным, так как элементы F - строки отрицательны. Отрицательные числа свидетельствуют не только о возможности увеличения общей стоимости производимой продукции, но и показывает, на сколько увеличится эта сумма при ведении в план того или другого вида продукции Так, число - 9 означает, что при включении в план производства одного изделия А обеспечивается увеличение выпуска продукции на 9 грн. Если включить в план производство по одному изделию В и С, то общая стоимость изготовленной продукции возрастает соответственно на 10 и16 грн. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделия С.
Т.о., в качестве разрешающего столбца выбирается столбец х3. Для выбора разрешающей стоки необходимо каждый свободный член разделить на соответствующее значение столбца х3 ( при этом необходимо учитывать знаки). Q = MIN(360/12;192/8;180/3)=192/8=24.
Числу 24 соответствует вторая строка, которая и является разрешающей. Найдя число 24, мы с экономической точки зрения определили, какое количество изделий С предприятие может изготовить с учетом норм расхода и имеющихся объемов сырья каждого вида, т.к. сырья каждого вида соответственно имеется 360,192,180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12,8,3 кг., то максимальное число изделий С которое может быть изготовлено предприятием = MIN = 24 т.е. ограничивающим фактором для производства изделий С является имеющийся объем сырья второго вида. Сырье будет полностью израсходовано . Перейдем к следующей таблице
Таблица 5.
|
-х1 |
-x2 |
у2 |
св.член |
|
|||||
Y1 |
9 |
9 |
-1,5 |
72 |
72 - это неиспользованное сырье |
|||||
-х3 |
0,75 |
0,5 |
0,125 |
24 |
|
|||||
у3 |
2,75 |
1,5 |
-0,375 |
108 |
108-это неиспользованное сырье 3-го вида |
|||||
F |
3 |
-2 |
2 |
384 |
384- стоимость всей произведенной прод-и. |
|||||
При данном плане производства изготовляется 24 изделия С.
Экономическая интерпретация столбца 2 : 0,5 показывает насколько следует уменьшить изготовление изделия С, если запланировать выпуск одного изделия В. 9 и 1,5 - показывают сколько потребуется сырья 1-го и 3-го вида при включении в план производства одного изделия В , а 2 показывает, если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции на 2 грн., т.е., если включить в план производства продукции 1 изделия В, то это потребует уменьшение выпуска изделия С на 0,5 , доп. затрат сырья 1-го вида -9кг., сырья 2-го вида -1,5 кг., а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастает на 2 грн. ( раньше нормы затрат сырья 1-го и 2-го вида были 15 и 3) - это объясняет уменьшение изделия С. Аналогично дается экономическая интерпретация столбца х1.
Несколько иное экономическое содержание имеет столбец х3. Число 0,125 показывает, что увеличение объемов сырья 2-го вида на 1 кг. Позволило бы увеличить выпуск изделий С на 0,125 ед. Одновременно потребовалось бы 1,5 кг сырья 1-го вида и 0,375 кг сырья 3-го вида. Увеличение выпуска изделия С на 0,125 приведет к росту выпуска продукции на 2 грн. Ясно, что найденный план не оптимальный. Отрицательный член свидетельствует, что в следующем плане следует предусмотреть выпуск изд. В. Q = MIN ( 72/9;24/0,5;108/1,5)=72/9=8
Следовательно выпуск изделия В ограничен сырьем 1-го вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий В.
Переходим к следующей симплекс - таблице.
Таблица 6.
|
-х1 |
у1 |
у2 |
св.член |
-x2 |
1 |
0,11 |
-0,017 |
8 |
-х3 |
0, 0.25 |
-0,06 |
0,208 |
20 |
у3 |
1,25 |
-0,17 |
-0,125 |
96 |
F |
5 |
0,22 |
1,67 |
400 |
В F - строке нет отрицательного члена, следовательно этот план оптимальный.
План выпуска продукции, включающий 8 изделий В и 20 изделий С, является оптимальным.
При данном плане выпуска изделий полностью используется сырье 1-го и 2-го вида и остается неиспользованным 96 кг. сырья 3-го вида, а стоимость производимой продукции = 400 грн. Оптимальным планом не предусматривается изготовление изделия ш. Число 5 показывает, что при данном плане включения в него выпуска ед. изд. А приводит лишь к уменьшению общей величины стоимости на 5 грн.
Задание 4.
Используя экспертные оценки определить согласованность экспертов на основе расчета коэффициента конкордации и определить степень влияния факторов на результирующий показатель.
пример
Для формирования первоначального набора технико-экономических показателей, влияющих на рост производительности труда на машиностроительных и металлообрабатывающих предприятиях Гомеля, работникам отделов труда и заработной платы заводов “Центролит”, пусковых двигателей, станкостроительного имени С.М. Кирова, измерительных приборов была роздана анкета. В анкете первого тура указывалось: “В целях изыскания резервов роста производительности труда на Вашем предприятии предлагаем Вам указать по 5 технико-экономических показателей, оказывающих, по Вашему мнению наибольшее влияние на рост производительности труда”. Так как мнения опрашиваемых специалистов-экспертов не совпали полностью, то в первоначальный набор вошли 9 технико-экономических показателей работы предприятия:Х1 - машиновооруженность рабочих, грн.; Х2 - фондовооруженность рабочих, грн.; Х3 -электровооруженность рабочих, кВт.ч; Х4- энерговооруженность рабочих, Гкал; Х5 - интегральный коэффициент работы оборудования; Х6 - использование баланса рабочего времени (отработано рабочим чел/дней); Х7 - социально-экономические факторы (разряд, стаж, уровень образования и т.д.); Х8 - условия труда на рабочем месте (освещенность, загазованность, шум, вибрация и т.д.); Х9- специализация предприятия, коэффициент.
Все они были внесены в анкету второго тура, розданную тем же экспертам-специалистам, с предложением проранжировать влияние этих технико-экономических показателей на рост производительности труда, (технико-экономическому показателю, оказывающему наибольшее влияние на рост производительности труда присваивается ранг 1, следующему 2, далее 3 и 4 и т.д. (случай несвязанных рангов)). Если же эксперт затрудняется разграничить влияние каких-то показателей на рост производительности труда, то присваивает им одинаковые ранги (случай развитых рангов). Ответы экспертов сводятся в матрицу рангов, где m - количество экспертов; n - количество технико-экономических показателей-факторов.
Степень согласованности мнений специалистов характеризует коэффициент конкордации w, величина которого изменяется от 0 до 1 (w=0 мнения экспертов не совпадают, w=1 - полностью совпадают).
Наличие (отсутствие) связанных рангов обусловливает методику определения коэффициента конкордации, характеризующего степень согласованности мнений экспертов. При анализе анкет по отдельным заводам имелись случаи наличия связанных (завод “Центролит”) (табл. 7) рангов в ответах экспертов. Методика расчёта коэффициента конкордации w в случае связанных рангов состоит в следующем.
Складываются порядковые номера мест факторов.
Полученная сумма рангов делится на количество связанных факторов.
Каждому связанному фактору присваивается ранг, полученный в результате переранжировки.
Последующим фактором присваивается очередной номер, не участвовавший в предыдущих расчетах.
Таблица 7. Матрица рангов ответов экспертов литейного завода “Центролит”.
Факторы |
Эксперты |
||||
|
1 |
2 |
3 |
4 |
5 |
X1 |
1 |
1 |
1 |
1 |
1 |
X2 |
5 |
4 |
2 |
4 |
4 |
X3 |
2 |
1 |
2 |
2 |
2 |
X4 |
5 |
4 |
4 |
4 |
4 |
X5 |
4 |
3 |
4 |
3 |
3 |
X6 |
2 |
1 |
1 |
2 |
3 |
X7 |
3 |
2 |
3 |
2 |
2 |
X8 |
3 |
2 |
3 |
2 |
2 |
X9 |
5 |
3 |
4 |
4 |
4 |
å |
30 |
21 |
24 |
24 |
25 |
Переранжировка рангов факторов в первом столбце табл. 1. Ранг фактора Х1=1; Х3=Х6=(2+3)/2=2.5; Х7=Х8=(4+5)/2=4.5; Х5=6; Х2=Х4=Х9=(7+8+9)/3=8.
В остальных столбцах переранжировки факторов осуществляется аналогично. Результаты переранжировки сводятся в матрицу переранжированных рангов (табл.8).
Таблица 8. Матрица переранжировки рангов.
Факторы |
Эксперты |
|
|
|
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
X1 |
1 |
2 |
1,5 |
1 |
1 |
6,5 |
-18,5 |
342,25 |
X2 |
8 |
8,5 |
3,5 |
8 |
8 |
36 |
+11 |
121 |
X3 |
2,5 |
2 |
3,5 |
3,5 |
4,5 |
14,5 |
-10,5 |
110,25 |
X4 |
8 |
8,5 |
8 |
8 |
8 |
40,5 |
+15,5 |
240,25 |
X5 |
6 |
6,5 |
8 |
6 |
5,5 |
32 |
+7 |
49 |
X6 |
2,5 |
2 |
1,5 |
3,5 |
5,5 |
15 |
-10 |
100 |
X7 |
4,5 |
4,5 |
5,5 |
3,5 |
3 |
21 |
-4 |
16 |
X8 |
4,5 |
4,5 |
5,5 |
3,5 |
3 |
21 |
-4 |
16 |
X9 |
8 |
6,5 |
8 |
8 |
8 |
38,5 |
+13,5 |
182,25 |
å |
45 |
45 |
45 |
45 |
45 |
225 |
|
1117 |
1. Суммы рангов столбцов после переранжировки должны быть равны между собой-45.
2. Подсчитываются суммы рангов каждой в отдельности взятой строки и всех строк.
3. Сумма рангов столбцов должна быть равна сумме рангов строк - 225 (графа 7, табл. 8).
4. Определяется средний ранг фактора
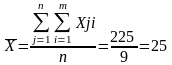
5. Определяется величина S (графа 9 табл.8):
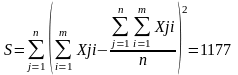
6. Формула коэффициента конкордации имеет вид
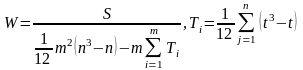
где t - число связанных рангов в каждом отдельно взятом столбце матрицы рангов,
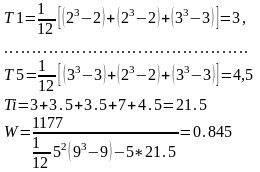
7. Для определения значимости коэффициента конкордации исчисляется критерий X2 (Пирсона) с числом степеней свободы n-1:
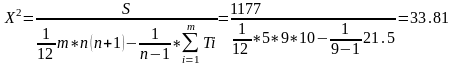
Значение X2 сравнивается с табличным X2T. Величина X2 должна быть больше X2T. Так как X2 > X2T при 5%-ном уровне значимости, то нулевую гипотезу случайности совпадений мнений экспертов следует считать отвергнутой.
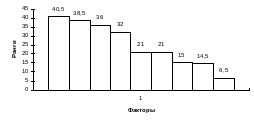
Рис.2 Гистограмма распределения факторов по степени их влияния на рост производительности труда на заводе “Центролит”
8. Строится гистограмма распределения факторов степени их влияния на рост производительности труда (графа 7 табл. 8) и дается ее анализ.
Из данных табл. 8 и рис. 2 видно, что влияние факторов на рост производительности труда на заводе “Центролит” распределяется следующим образом: Х1, Х3, Х6, Х7, Х8, Х5, Х2, Х9, Х4.
Данное распределение почти такое же, как и на заводе пусковых двигателей (замены места только рядом стоящих факторов Х3 с Х6 и Х4 с Х9). На других промышленных предприятиях, где проводился опрос специалистов, распределение факторов по степени влияния на рост производительности труда аналогично
Задание 5.
Используя один из методов решения задач теории игр - метод итераций (Брауна-Робинсона) выбрать оптимальные стратегии игроков и найти оптимальную цену игры.
пример
Два игрока А и В одновременно и не сговариваясь, показывают один, два или три пальца. Выигрыш решает общее количество пальцев если оно четное, выигрывает А и получает у В сумму, равную этому числу; если нечетное, то наоборот, А платит В сумму, равную этому числу. Как поступать игрокам?
Составим матрицу игры
Таблица 9
-
В1
В2
В3
ai
А1
2
-3
4
-3
А2
-3
4
-5
-5
А3
4
-5
6
-5
b
j4
4
6
(min) max
Рассмотрим один из самых простых методов решения игр – метод итераций (метод Брауна – Робинсона). Идея его в следующем в игре стороны А и В применяют поочередно свои стратегии, на каждом шаге итерационного процесса каждый игрок отвечает на очередной ход другого той своей стратегией, которая является оптимальной для него относительно смешанной стратегией другого, в которую все примененные до сих пор стратегии входят пропорционально частотам их применения. Вместо того чтобы вычислять каждый раз средний выигрыш, можно пользоваться просто “накопленным” за предыдущие ходы выигрышем и выбирать ту свою стратегию, при которой этот накопленный выигрыш максимален (минимален). Доказано, что такой метод сходится при увеличении числа “партий” средний выигрыш на одну партию будет стремиться к цене игры, а частоты применения стратегий – к их вероятностям в оптимальных смешанных стратегиях игроков.
Пример таблицу 9 преобразуем в положительную, чтобы не иметь дело с отрицательными числами; прибавим “5”, получим таблицу 10. Начнем с произвольно выбранной стратегии А, например А3.
Таблица 10.
-
В1
В2
В3
А1
7
2
9
А2
2
9
0
А3
9
0
11
В 1 столбце – номер партии К
Во 2 столбце – N i стратегии игрока А
В 3,4,5, - накопленный выигрыш за первые К партии при тех стратегиях, которые применяли 7,8,9 игроки в предыдущих партиях.
Из этих накопленных выигрышей подчеркнут минимальный (если несколько – подчеркнуть все). Подчеркнутое число определяет ответный выбор игрока В в данной партии – он выбирает ту стратегию, которая соответствует подчеркнутому числу (если несколько – берется любая). Таким образом определяется номер j оптимальной (в данной партии) стратегии В (ставиться в следующем столбце). В последующих трех столбцах дается накопленный выигрыш за К партий соответственно при стратегиях А1, А2, А3 игрока А (получается прибавлением элементов столбца Вj ê тому что было строкой выше). Из этих значений в таблице 11 подчеркнуто максимальное; оно определяет выбор стратегии игрока А в следующей партии. В последующих столбцах даны
V- нижняя оценка цены игры, равная минимальному накопленному выигрышу, деленному на число партий К;
`V – верхняя оценка цены игры, равная максимальному накопленному выигрышу, деленному на К;
V* - среднее арифметическое между ними (оно служит лучшей, чем нижняя и верхняя, приближенной оценкой цены игры);
! Как видно, величина V* незначительно колеблется около цены игры V – 5. Подсчитаем по таблице 11 частоты стратегий игроков
~p1 = 4/15 = 0 ~p2 = 7/15 = 0,468; ~p3 = 4/15 = 0,266;
~q1 = 2/15 = 0,133; ~q2 = 8/15 = 0,534; ~q3 = 5/15 = 0,333,
что не так уж сильно отличается от вероятностей p1, p2, p3, q1 q2, q3. Такие приближения получены уже при 15 итерациях – это хорошее приближение.
Важным преимуществом итерационного метода решения игр является то, что его трудоемкость сравнительно медленно возрастает с увеличением размерности игры m*n, тогда как трудоемкость метода линейного программирования растет при увеличении размерности задачи гораздо быстрее.
|
Mатрица игры |
|
|
|
Mатрица игры |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
А В |
B1 |
B2 |
B3 |
ai |
|
|
|
А В |
B1 |
B2 |
B3 |
|||||||||||||||||||||||||||||||||||||
A1 |
2 |
-3 |
4 |
-3 |
|
|
|
A1 |
7 |
2 |
9 |
|||||||||||||||||||||||||||||||||||||
A2 |
-3 |
4 |
-5 |
-5 |
|
|
|
A2 |
2 |
9 |
0 |
|||||||||||||||||||||||||||||||||||||
A3 |
4 |
-5 |
6 |
-5 |
|
|
|
A3 |
9 |
0 |
11 |
|||||||||||||||||||||||||||||||||||||
bj |
4 |
4 |
6 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Метод итерации (Брауна - Рoбинсона) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Таблица 11 |
|
|
||||||||||||||||||||||||||||||||||||||
k |
i |
B1 |
B2 |
B3 |
j |
A1 |
|
A3 |
v |
v |
v* |
|||||||||||||||||||||||||||||||||||||
1 |
3 |
9 |
0 |
11 |
2 |
2 |
9 |
0 |
0 |
9 |
4,5 |
|||||||||||||||||||||||||||||||||||||
2 |
2 |
11 |
9 |
11 |
2 |
4 |
18 |
0 |
4,5 |
9 |
6,75 |
|||||||||||||||||||||||||||||||||||||
3 |
2 |
13 |
18 |
11 |
3 |
13 |
18 |
11 |
3,67 |
6 |
4,84 |
|||||||||||||||||||||||||||||||||||||
4 |
2 |
15 |
27 |
11 |
3 |
22 |
18 |
22 |
2,75 |
5,5 |
4,13 |
|||||||||||||||||||||||||||||||||||||
5 |
1 |
22 |
29 |
20 |
3 |
31 |
18 |
33 |
4 |
6,6 |
5,3 |
|||||||||||||||||||||||||||||||||||||
6 |
3 |
31 |
29 |
31 |
2 |
33 |
27 |
33 |
4,84 |
5,5 |
5,17 |
|||||||||||||||||||||||||||||||||||||
7 |
1 |
38 |
31 |
40 |
2 |
35 |
36 |
33 |
4,43 |
5,14 |
4,79 |
|||||||||||||||||||||||||||||||||||||
8 |
2 |
40 |
40 |
40 |
2 |
37 |
45 |
33 |
5 |
5,61 |
5,3 |
|||||||||||||||||||||||||||||||||||||
9 |
2 |
42 |
49 |
40 |
3 |
46 |
45 |
44 |
4,45 |
5,11 |
4,78 |
|||||||||||||||||||||||||||||||||||||
10 |
1 |
49 |
51 |
49 |
1 |
53 |
47 |
53 |
4,9 |
5,3 |
5,1 |
|||||||||||||||||||||||||||||||||||||
11 |
3 |
58 |
51 |
60 |
2 |
55 |
56 |
53 |
4,64 |
5,09 |
4,87 |
|||||||||||||||||||||||||||||||||||||
12 |
2 |
60 |
60 |
60 |
2 |
57 |
65 |
53 |
5 |
5,41 |
5,2 |
|||||||||||||||||||||||||||||||||||||
13 |
2 |
62 |
69 |
60 |
3 |
66 |
65 |
64 |
4,61 |
5,07 |
4,84 |
|||||||||||||||||||||||||||||||||||||
14 |
1 |
69 |
71 |
69 |
1 |
73 |
67 |
73 |
4,93 |
5,21 |
5,07 |
|||||||||||||||||||||||||||||||||||||
15 |
3 |
78 |
71 |
80 |
2 |
75 |
76 |
73 |
4,74 |
5,06 |
4,9 |
|||||||||||||||||||||||||||||||||||||