3. Комбінування методів просторового покращення

За деякими виключеннями, як, наприклад, у разі комбінації згладжування з пороговим перетворенням, до даного моменту увага приділялася лише кожному з методів покращення окремо. Проте при рішенні конкретних завдань для досягнення прийнятних результатів може знадобитися застосування декількох взаємодоповнюючих методів покращення. У цьому розділі на окремих прикладах буде проілюстровано, як скомбінувати окремі підходи для вирішення складнішого завдання покращення.

Зображення на рис. 4.15(а) є повний знімок скелета, що отриманий за допомогою гамма-променів, використовується для виявлення таких захворювань, як кісткові інфекції і пухлини. Метою є покращення цього зображення шляхом підвищення його різкості й детальнішого виявлення елементів скелета. Малий динамічний діапазон рівнів яскравості й високий вміст шуму роблять це зображення важким для покращення. Стратегія полягає у використанні лапласіана для виділення дрібних деталей, і градієнта для покращення країв, що виступають. З причин, які будуть пояснені нижче, згладжена копія градієнтного зображення використовуватиметься для маскування лапласіана. У кінці, для збільшення динамічного діапазону яскравості, використовуватиметься градаційне перетворення.

На рис. 4.15(б) показаний лапласіан, отриманий фільтрацією початкового зображення з використанням маски на рис. 4.8(г). Для кращого відтворення це зображення було піддане градаційній корекції, як і зображення на рис. 4.9. Різкіше зображення можна отримати простим складанням зображень на рис. 4.15(а) і (б), що буде реалізацією другого рядка рівняння (4.9), оскільки використовувалася маска з позитивним центральним коефіцієнтом. Вже дивлячись на рівень шумів на зображенні (б) можна чекати, що складання зображень рис. 4.15(а) і (б) призведе до отримання різкішого, але дуже зашумленого зображення, що і підтверджується результатом, показаним на рис. 4.15(в). Зменшити рівень шуму можна було б за допомогою медіанного фільтру. Проте медіанна фільтрація є нелінійною операцією, здатною видалити деталі зображення, що неприйнятно під час обробці медичних зображень.

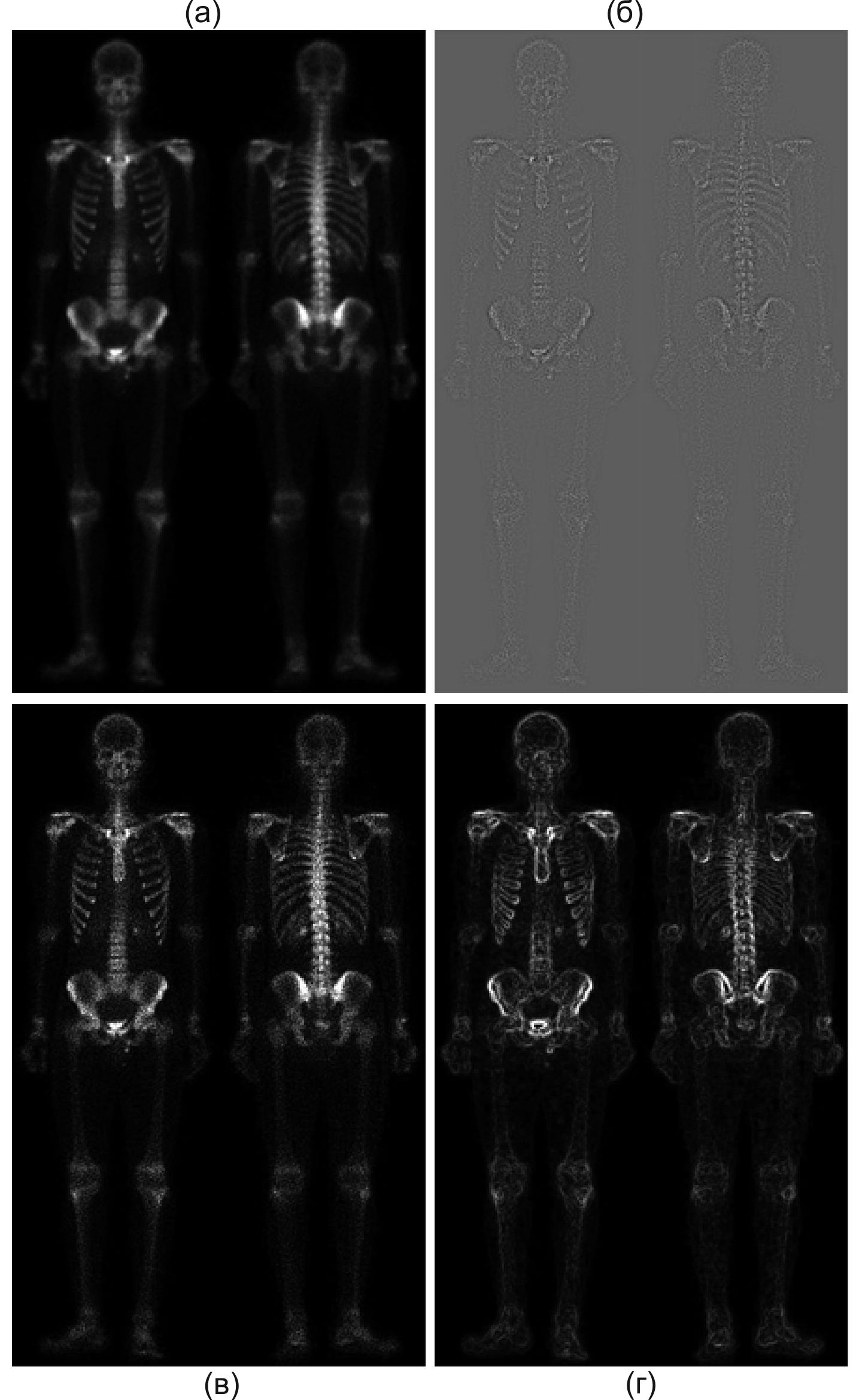
Рис. 4.15. (а) Повний знімок скелета, отриманий за допомогою гамма-променів; (б) застосування оператора лапласіана до зображення (а); (в) підвищення різкості складанням зображень (а) і (б); (г) застосування оператора Собела до зображення (а)

Альтернативним підходом є використання маски, що формується шляхом згладжування градієнта початкового зображення. Це неважко пояснити на підставі властивостей першої і другої похідних. Лапласіан, будучи оператором другої похідної, має ту безперечну перевагу, що є прекрасним способом покращення дрібних деталей. Проте через це він посилює шум в значно більшій мірі, ніж градієнт. Цей шум є виразним на гладких областях. Градієнт, в порівнянні з лапласіаном, дає сильніший відгук в областях зі значними змінами яскравості (на переходах яскравості і сходинках).

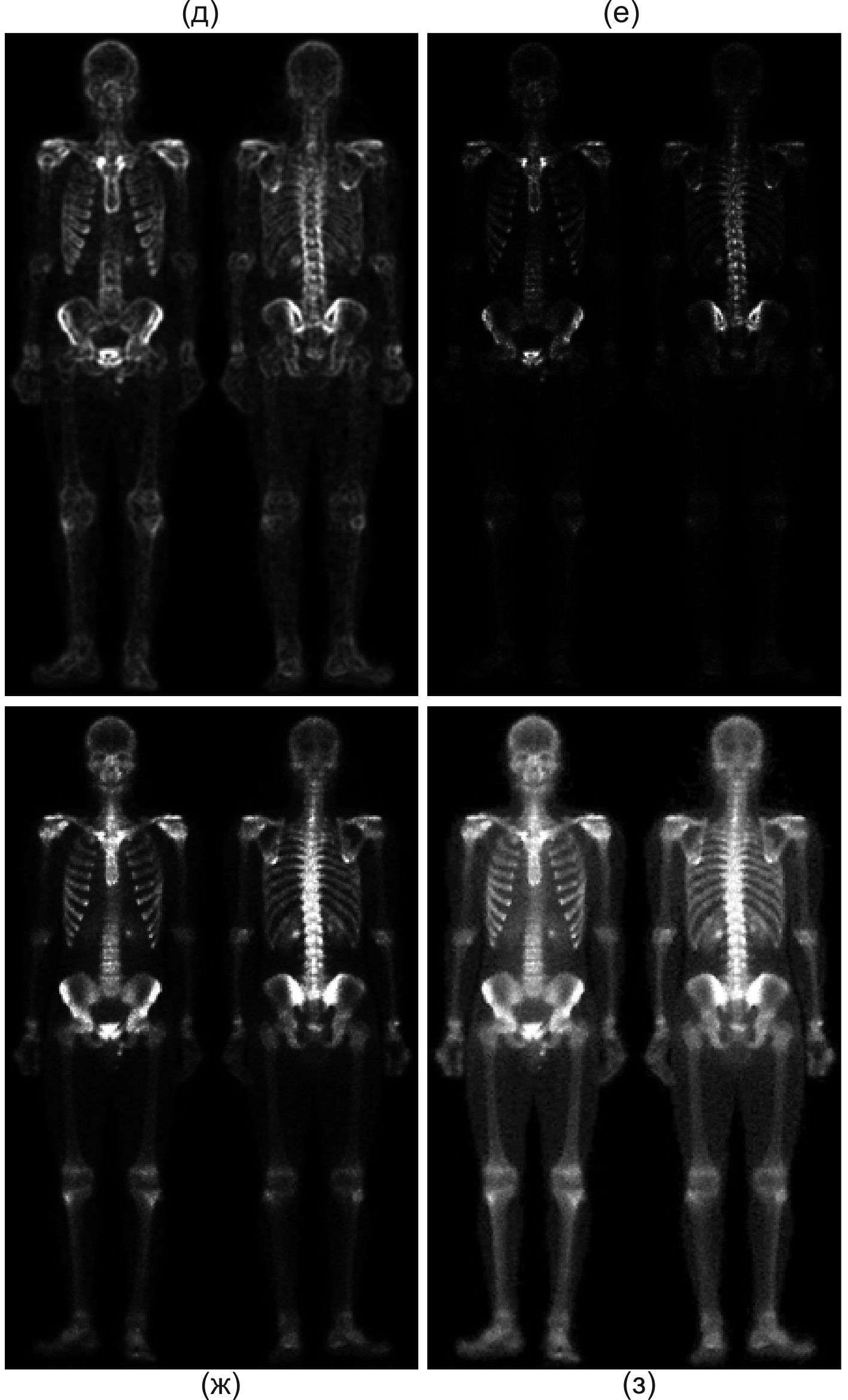
Рис. 4.15. (д) Зображення (г), згладжене усереднюючим фільтром по околиці 5x5; (е) зображення-маска, отримане перемножуванням зображень (в) і (д); (ж) зображення з підвищеною різкістю, отримане складанням зображень (а) і (е); (з) кінцевий результат, отриманий із зображення (ж) градаційною корекцією за степеневим законом. Порівняйте зображення (ж) і (з) із початковим зображенням (а)

Відгук градієнта на шум і дрібні деталі слабкіший, ніж у лапласіана, і до того ж надалі може бути понижений шляхом згладжування градієнта усереднюючим фільтром. Тим самим, ідея зводиться до згладжування градієнта і множення його на зображення-лапласіан. У цьому контексті можна розглядати градієнт як зображення-маску. Їх створення дозволить зберегти деталі в областях зміни яскравості й подавити шум на відносно плоских ділянках. Цей процес може бути грубо представлений як об’єднання кращих якостей лапласіана і градієнта. Результат множення додається до початкового зображення, щоб отримати остаточне зображення з підвищеною різкістю, і навіть може використовуватися як варіант фільтрації з підвищенням високих частот.

На рис. 4.15(г) показаний градієнт, отриманий фільтрацією початкового зображення оператором Собела за формулою (4.18). Компоненти і , були отримані з використанням масок, показаних на рис. 4.13(г) і (д) відповідно. Як і слід було чекати, контури на цьому зображенні виділяються значно сильніше, ніж на зображенні-лапласіані. Згладжене градієнтне зображення, представлене на рис. 4.15(д), було отримане з використанням усереднюючого фільтру розмірами 5x5. Обидва градієнтних зображення перед відтворенням були піддані тому ж градаційному перетворенню, що й зображення-лапласіан. Оскільки на градієнтному зображенні найменше допустиме значення дорівнює 0, фон на цьому зображенні залишається чорним, а не сірим, як у разі лапласіану на рис. 4.15(б). Той факт, що зображення на рис. 4.15(г) і (д) виглядають значно яскравішими, ніж зображення на рис. 4.15(б), є очевидним слідством того, що на зображенні зі значним вмістом контурів, градієнт, як правило, має більш високі значення, ніж лапласіан.

Результат множення лапласіана й згладженого градієнта показаний на рис. 4.15(е). Помітне переважання різких контурів і відносне зниження рівня шуму, що і було основною метою маскування лапласіана згладженим градієнтним зображенням. Збільшення отриманого добутку до початкового зображення дає в результаті зображення з підвищеною різкістю, показане на рис. 4.15(ж). Значне підвищення різкості деталей в порівнянні з початковим зображенням помітне на більшій частині даного зображення, включаючи ребра, хребет, таз і череп. Таке поліпшення недосяжне під час використання одного тільки лапласіана або градієнта.

Розглянута процедура підвищення різкості не впливає в помітним чином на динамічний діапазон яскравості зображення. Таким чином, фінальний крок в цьому завданні покращення полягає у збільшенні динамічного діапазону отриманого результату. Як було детально розглянуто, існує безліч функцій градаційної корекції, які дозволяють досягти цієї мети. Вдомо, що еквалізація гістограми ймовірно не дасть добрі результати на зображеннях, розподіл яскравості яких зсунуто в область чорного, як на зображеннях з цього прикладу. Рішенням могло б стати задання гістограми, проте загальний чорний фон зображення, з яким доводиться мати справу, примушує зробити вибір на користь степеневого перетворення. Оскільки потрібно розтягування рівнів яскравості, то, значення повинно бути меншим за 1. Декілька експериментів з різними значеннями параметрів дозволяють отримати остаточний результат, показаний на рис. 4.15(з), при і Порівняння цього зображення із зображенням на рис. 4.15(ж) показує, що стала помітна значна кількість елементів. Структура кісток скелета, включаючи кістки рук і ніг, також стала виразнішою. На початковому зображенні дуже слабо видно контури тіла і м’які тканини. "Витягування" подібних деталей за допомогою розтягування динамічного діапазону яскравості посилює також і шум, але, проте, можна відмітити, що на рис. 4.15(з) є значне візуальне покращення початкового зображення.

Лекція 5. Фур’є аналіз. Фільтрація в частотній області

Мета: Метою даної лекції є формування знань про Фур’є аналіз двовимірних сигналів (зображень) та основи фільтрації в частотній області.

План: 1. Одно- і двовимірне перетворення Фур’є; 2. Фільтрація в частотній області.

Вступ

Французький математик Жан Батіст Жозеф Фур’є народився в 1768 р. в місті Осер на півдорозі з Парижа в Діжон. Головне наукове досягнення Фур’є, завдяки якому він залишився в пам’яті нащадків, було схематично викладено ним у мемуарах 1807р і повністю опубліковано в 1822р в його книзі «Аналітична теорія тепла» (La Theorie Analitique dc la Chaleur). Результат Фур'є, що відноситься до предмету розгляду цієї лекції, полягає, по суті, в тому, що будь-яка функція, що періодично відтворює свої значення, може бути представлена у вигляді суми синусів і (або) косинусів різних частот, помножених на деякі коефіцієнти (тепер ця сума носить назву ряд Фур’є). Складність поведінки функції при цьому не має значення. Якщо тільки функція є періодичною і задовольняє необтяжливим математичним умовам, вона може бути представлена у вигляді вищевказаної суми. В даний час це твердження є загальновизнаним, однак у момент своєї появи це була революційна ідея, на «звикання» до якої математикам всього світу потрібно більше століття. У той час оплотом математичного мислення було поняття регулярності функцій. З таких позицій ідея про те, що складна функція може бути представлена у вигляді суми простих (синусів і косинусів), здавалася далеко не очевидною (Рис. 5.1). Тому не дивно, що ідеї Фур’є в цьому відношенні були зустрінуті скептично.

Коли функція не є періодичною (але площа під її графіком скінченна), вона може бути виражена у вигляді інтеграла від синусів і (або) косинусів, помножених на деяку вагову функцію. У такому випадку ми маємо справу з перетворенням Фур’є, яке в більшості практичних задач виявляється навіть більш корисним, ніж ряд Фур’є. Обидва уявлення мають важливу характерну особливість. Функція, задана як рядом, так і перетворенням Фур’є, може бути повністю, без втрати інформації, відновлена (реконструйована) за допомогою деякої процедури обернення. Ця властивість є однією з важливих властивостей розглянутих представлень, оскільки вона дозволяє працювати в «фур’є-області», а потім повернутися у вихідну область визначення функції без втрати будь-якої інформації.

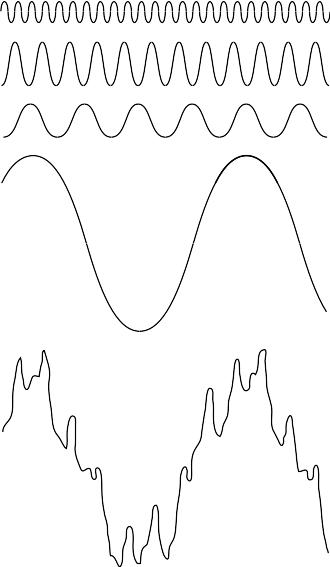
Рис. 5.1. Нижня функція є сумою чотирьох розташованих над нею функцій

У кінцевому рахунку, саме ефективність застосування апарату рядів і перетворення Фур’є для вирішення практичних завдань перетворила його в фундаментальний інструмент, який широко використовується і досліджується.

Оскільки ми будемо мати справу тільки з функціями (зображеннями) кінцевої протяжності, нас буде цікавити саме перетворення Фур’є. Показано, що методи фур’є-аналізу дають ясні за змістом і практичні способи вивчення і реалізації сукупності підходів для покращення зображень.

В даній лекції акцент зроблений на дискретний варіант перетворення та деякі його властивості.