Лекція 4. Основи просторової фільтрації
Мета: Метою даної лекції є дослідження основних методів просторової фільтрації для покращення цифрових зображень.
План: Лінійна фільтрація. Фільтри, що базуються на порядкових статистиках. Фільтри підвищення різкості. Комбінування методів просторового покращення зображень.
Вступ
Як вже зазначалося, деякі локальні перетворення оперують одночасно як зі значеннями пікселів в околиці, так і з відповідними значеннями деякої матриці, що має ті самі розміри, що й околиця. Таку матрицю називають фільтром, маскою, ядром, шаблоном або вікном, причому перші три терміни є найбільш поширеними. Значення елементів матриці прийнято називати коефіцієнтами.
Взагалі кажучи, фільтрація тісно пов’язана з застосуванням перетворення Фур’є та обробкою сигналів у частотній області. У даній лекції нас цікавитимуть операції фільтрації, які виконуються безпосередньо над елементами зображення. Для подібних операцій використовується термін просторова фільтрація, на відміну від більше традиційної фільтрації в частотній області.
Схема
просторової фільтрації ілюструється
на рис. 4.1. Процес ґрунтується на простому
переміщенні маски фільтру від точки до
точки зображення; у кожній точці
відгук
фільтру
обчислюється з використанням заздалегідь
заданих зв’язків. У випадку лінійної
просторової
фільтрації відгук задається сумою
добутків коефіцієнтів фільтру на
відповідні значення пікселів в області,
що вкрита маскою фільтру.
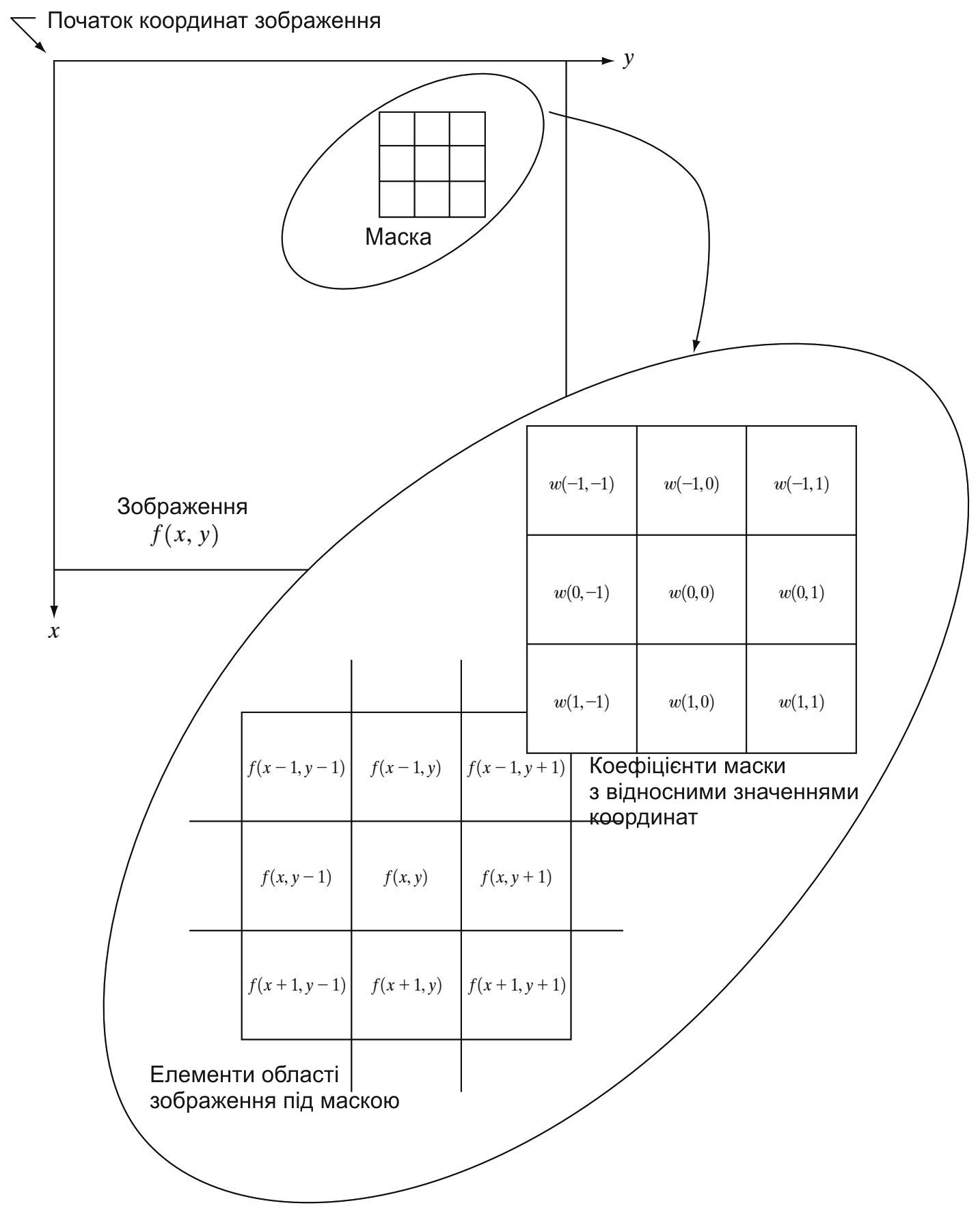
Рис. 4.1. Схема просторової фільтрації. Збільшені малюнки представляють маску 3x3 і фрагмент зображення безпосередньо під нею; для наочності фрагмент зображення показаний дещо зміщеним відносно маски
Для
маски 3x3 елементи, показаної на рис. 4.1,
результат (відгук)
лінійній фільтрації в точці
зображення складе
),
що,
як видно, є сумою добутків коефіцієнтів
маски на значення пікселів безпосередньо
під маскою. Зокрема відмітимо, що
коефіцієнт
знаходиться при значенні
,
вказуючи тим самим, що маска центрована
в точці(х,
у).
У випадку маски розмірами mхn
вважатимемо, що
де
і
- позитивні цілі. Це означає, що надалі
розглядатимуться маски непарних
розмірів,
причому найменшою буде маска 3x3
елементи(маска розмірами 1x1 елемента
буде виключено як тривіальна).
Фільтрація
зображення
розміром
за допомогою фільтру розміром
задається
виразом загального вигляду :
(4.1)
де,
як випливає з попереднього абзацу,
і
.
Під час фільтрації усього зображення
ця формула має бути розрахована для
усіх комбінацій
і
.
Це означає, що усі елементи зображення
будуть оброблені заданою маскою. Легко
перевірити, що при
ця формула зводиться до формули,
приведеної ву попередньому абзаці.
Процедура лінійної фільтрації, що задається рівнянням (4.1), в частотній області аналогічна операції згортки. З цієї причини лінійну просторову фільтрацію часто називають "згортка маски з зображенням". Аналогічно, маску фільтру іноді називають маскою згортки або ядром згортки.
У разі, коли інтерес представляє тільки значення відгуку R по масці в точці , а не схема реалізації маски згортки, іноді використовують наступний вираз:
(4.2)
де
-
коефіцієнти маски,
- значення пікселів, що відповідають
цим коефіцієнтам, а
- загальне число коефіцієнтів у масці.
Для маски 3x3, що представлена на рис.
4.2, відгук в точці
(х,
у) зображення має вигляд
(4.3)
Спеціальна увага, що приділяється цій простій формулі, пояснюється тим, що вона часто зустрічається в літературі з обробки зображень.
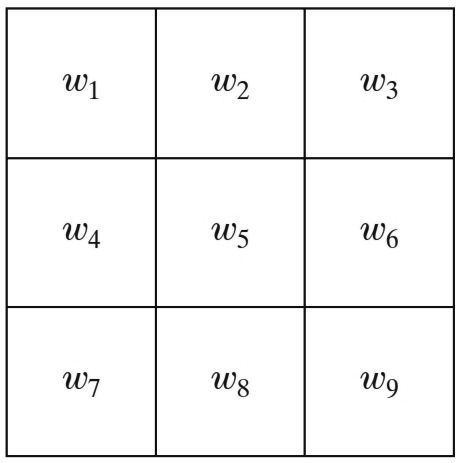
Рис. 4.2. Інший варіант представлення маски фільтру по околиці 3x3 елементи