1.7.5 Расчёт прогиба панели перекрытия.

Предельный прогиб см.

Вычисляем параметры, необходимые для определения прогиба плиты с учетом трещин в растянутой зоне.

Заменяющий момент равен изгибающему моменту от постоянной и длительной нагрузок M = 68,29 кН·м. Суммарная продольная сила равна усилию предварительного обжатия с учетом всех потерь и при _sp = 1: кН. Коэффициент _es = 0,8 — при длительном действии нагрузки.

Эксцентриситет:

м.

Коэффициент:

.

Коэффициент (отношение средних деформаций растянутой арматуры на участке между трещинами к деформациям в сечении с трещиной):

,

.

Кривизна оси при изгибе:

, где:

_b — коэффициент, характеризующий неровности деформаций бетона сжатой зоны на участках между трещинами, _b = 0,9;

 — коэффициент, зависящий от характера действия нагрузки и условий эксплуатации конструкции: при длительном действии нагрузки в условия средней относительной влажности воздуха  = 0,15;

см² — площадь бетона сжатой зоны

 6,88 · 10^–3 м^–1.

м^–1.

Вычисляем прогиб:

м  3,2 см  [f] = 3,225 см — прогиб не превышает предельного значения.

2.Проектирование ригеля

2.1. Сбор нагрузок на ригель

Задаемся размерами ригеля:

Высота ригеля:

h_p=L_p/10=56см — принимаем h_р = 60 см;

см — принимаем b_р = 20 см.

Нагрузка на ригель:

Вес плиты:

Вес 1 м погонного ригеля: кН/м.

Итого: кН/м.

2.2. Расчетная схема ригеля. Определение расчетных усилий

Расчетный пролет ригеля определяется с учетом конструкции стыка ригеля с колонной (см. рис. 1) по формуле:

Усилия от расчётных нагрузок:

кН·м,

кН.

Рис. 1. Определение расчетного пролета ригеля.

2.3. Компоновка поперечного сечения ригеля

Поперечные сечения ригеля 1–1 и 2–2 (см. рис. 1) показаны на рисунке 2:

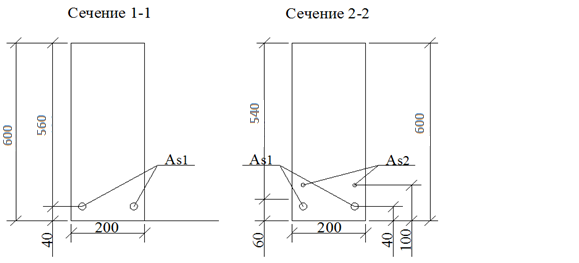
Рис. 2. Поперечные сечения ригеля.

а) Выберем материалы для ригеля:

Бетон:

класс B30;

расчётное сопротивление осевому сжатию R_b, МПа 17;

нормативное сопротивление осевому сжатию R_b,n, МПа 22;

расчётное сопротивление осевому растяжению R_bt, МПа 1,2;

нормативное сопротивление осевому растяжению R_bt,n, МПа 1,8;

начальный модуль упругости бетона E_b, МПа 32,5.

Арматура:

ненапрягаемая класса А-III;

нормативное сопротивление R_s,n, МПа 390;

расчётное сопротивление R_s, МПа 365;

модуль упругости E_s, МПа 200000

б) Подбор продольной рабочей арматуры.

Определяем рабочую высоту сечения: h₀ = 60 – 6 = 54 см.

Находим коэффициент α_m:

По таблице 3.1 [1] находим:  = 0,388;  = 0,806.

Характеристика сжатой зоны:

.

Относительная граничная высота сжатой зоны:

, — условие   _R выполнено.

Вычисляем площадь сечения растянутой арматуры:

см².

По приложению 6 [1] принимаем: A_s1 – 2 Ø28 A-III с площадью A_s = 12,32 см²; A_s2 — 2 Ø20 A-III с площадью A_s2 = 6,28 см². Суммарная площадь арматуры A_s = 18,6 см².

2.4 Определение точки обрыва верхней рабочей арматуры

Верхний продольный рабочий стержень каркаса ригеля обрывается в соответствии с изменением огибающей эпюры моментов.

Определяем относительную высоту сжатой зоны для сечения 1-1 по формуле:

,

По таблице 3.1 [1] определяем ₁ = 0,795

Вычисляем изгибающий момент, воспринимаемый сечением 1–1:

M₁ = R_s A_s h₀ ζ₁ = 365·10³·18,6·10^-4·0,54·0,795  291,45 кН·м.

Определяем относительную высоту сжатой зоны для сечения 2-2:

По таблице 3.1 [1] определяем ₂ = 0,87.

Вычисляем изгибающий момент, воспринимаемый сечением 2-2:

M₂ = R_s A_s1 h₀ζ₂ = 365·10³·12,32·10^-4·54·0,87  211,23 кН·м.

Расстояние z от точки опирания ригеля до точки теоретического обрыва арматуры определяем из уравнения момента от нагрузки на ригель:

Решив это уравнение, получаем z = 1,4 м.

Обрываемые стержни заводятся за точку теоретического обрыва на длину анкеровки ω, определяемую из условий:

1) ω ≥ 20d, ω ≥ 20·1,4 = 28 см = 0,28м

2) , где:

Q_y = Q_max – q  z — поперечная сила в точке теоретического обрыва арматуры ригеля,

Q_y = 214,7 – 82,57  1,4 =99,102 кН;

м.

Выбираем большее значение и округляем до целого числа ω = 70 см.