1.7.2 Определение потерь предварительных напряжений арматуры.

Коэффициент точности натяжения арматуры принимаем γ_sp = 1.

Потери от релаксации напряжений в арматуре при электротермическом способе натяжения МПа.

Потери от температурного перепада между натянутой арматурой и упорами ₂ = 0, так как при пропаривании форма с упорами нагревается вместе с изделием. Потери от деформации анкеров ₃ = 0 — при электротермическом натяжении. Потери от трения арматуры ₄ = 0, т.к. трение отсутствует. Потери от деформации стальных форм ₅ = 0, т.к. применяется электротермический способ натяжения арматуры.

Усилие обжатия:

кН.

Эксцентриситет усилия обжатия относительно центра тяжести сечения: см.

Напряжения в бетоне при обжатии:

кПа5,2 МПа.

Устанавливаем значение передаточной прочности бетона:

; МПа  0,5В25 — принимаем R_bp = 12,5 МПа. .

Вычисляем сжимающее напряжение в бетоне на уровне центра тяжести площади напрягаемой арматуры от усилия обжатия с учетом момента от собственного веса панели перекрытия M, равного:

кН·м.

кПа  1,797 МПа.

Потери от быстро натекающей ползучести:

при уровне напряжений ; ;

α — коэффициент, который учитывает более интенсивное развитие ползучести бетона с увеличением уровня напряжения:

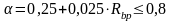, — условие выполняется.

₆ = 40 · 0,14  5,6 МПа.

Первые потери:

_los1 =₁ + ₆ = 14,16 + 5,6 = 19,76 МПа.

С учетом первых потерь усилия обжатия и напряжения в бетоне равны:

кН,

кПа  1,747 МПа,

 0,75.

Потери от релаксации напряжений в арматуре ₇ = 0.

Потери от усадки бетона ₈ = 35 МПа — по таблице 2.5 [1].

Потери от ползучести бетона:

— следовательно , где  = 0,85, т.к. панель перекрытия изготавливается при тепловой обработке и атмосферном давлении; МПа.

Вторые потери:

_los2 =₈ + ₉ = 35 + 17,85 = 52,85 МПа.

Полные потери:

_los =_los1 + _los2 = 19,76+52,85 =72,61 МПа.

Усилие обжатия с учетом полных потерь:

кН.

1.7.3 Расчет на образование трещин, нормальных к продольной оси.

Для элементов, к трещиностойкости которых предъявляют требования 3-й категории, принимаем значение коэффициентов по надёжности по нагрузке _f = 1.

Момент от полной нормативной нагрузки:

кН·м.

Вычисляем момент образования трещин по приближенному способу ядровых моментов:

, где

момент усилия обжатия относительно оси, проходящей через условную ядровую точку, наиболее удаленную от растянутой зоны:

кН·м;

кН·м.

Т.к. M > M_crc, то трещины образуются в растянутой зоне, следовательно необходим расчет по раскрытию трещин.

Проверяем, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэффициента точности натяжения _sp=1,15:

Изгибающий момент от веса плиты М=15,56 кН·м

Расчётное условие

P₁·γ_sp·(e_op-r_inf)-M< R_btp·W'_pl

P₁·γ_sp·(e_op-r_inf)-M=233,04·1,15·(0.927-0,08)-15,56=211,43 кН·см

R_btn·W'_pl=1,05 ·10845,15= 11387.25кН·см

211.43 < 11387.25 кН·см – условие удовлетворяется, начальные трещины не образуются.

1.7.4 Расчёт на раскрытие трещин, нормальных к продольной оси.

Предельная ширина раскрытия трещин: непродолжительных a_crc = 0,4 мм, продолжительных a_crc = 0,3 мм. Изгибающие моменты от нормативных нагрузок: суммарной M=68,29кН·м.

Приращение напряжений в арматуре от действия полной нагрузки:

, где

плечо внутренней пары сил:

см,

e_sp = 0 — т.к. усилие обжатия P приложено в центре тяжести площади нижней напрягаемой арматуры,

момент сопротивления сечения по растянутой арматуре:

см³.

кПа  127,519 МПа.

Ширина раскрытия трещин от действия полной нагрузки:

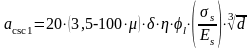, где:

коэффициент армирования сечения ;

 — коэффициент, принимаемый для изгибаемых элементов равным 1;

 — коэффициент, зависящий от вида и профиля продольной арматуры и равный для стержневой арматуры периодического профиля 1;

_l — коэффициент, учитывающий длительность действия нагрузки: при кратковременной нагрузке и непродолжительном действии постоянной и длительной нагрузок _l = 1, при продолжительном действии постоянной и длительной нагрузок для тяжелого бетона при нормальных условиях эксплуатации _l = 1,6 – 15 = 1,6 – 15 · 0,007  1,495.

мм.

Ширина раскрытия трещин от продолжительного действия длительной нагрузки

мм.

=0,14мм. a_crc = 0,3 мм.