6.2. Определение расчетных усилий

Расчетная схема второстепенной балки — многопролетная неразрезная балка.

Изгибающие моменты определяют с учетом перераспределения усилий:

В первом пролете:

кН·м,

На первой промежуточной опоре:

кН·м,

В средних пролетах и на средних опорах:

кН·м.

Отрицательный момент в среднем пролете для 14,63/7,45=1,96<3:

М=0,4 кН·м.

Поперечные силы:

На крайней опоре:

кН

На первой промежуточной опоре слева:

кН

На первой промежуточной опоре справа:

кН

6.3.Расчет прочности нормальных сечений.

а) Выберем материалы для второстепенной балки:

Бетон:

Как для плиты, класса Б 15.

Арматура:

продольная:

ненапрягаемая класса А-III;

нормативное сопротивление R_s,n, МПа 390;

расчётное сопротивление растяжению R_s, МПа 365;

расчётное сопротивление сжатию R_sc, МПа 365;

модуль упругости E_s, МПа 200000.

поперечная:

ненапрягаемая класса Вр-I;

диаметр, мм 5;

расчётное сопротивление растяжению R_s, МПа 260;

модуль упругости E_s, МПа 170000.

б) Уточнение высоты сечения второстепенной балки.

Расчет ведется с учетом образования пластического шарнира, , .

На опоре момент отрицательный — сжатая зона вверху. Сечение работает как прямоугольное с шириной ребра b = 0,25 м.

Находим h₀:

м

h = h₀ + a = 34 + 3,5 = 37,5 см — принимаем h_вб = 40 см.

В пролетах сечение тавровое – полка в сжатой зоне. Расчетная ширина полки при 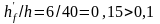равна м.

в) Подбор арматуры в первом пролете по М₁.

По табл.3.1 [1] вычисляем ; ;

Вычисляем площадь сечения растянутой арматуры:

м² = 6,6 см².

По приложению 6 [1] принимаем 2 Ø22 A-III с площадью A_s1 = 7,6 см²

Вычисляем сечения арматуры в среднем пролете:М₂=54,77

м² = 4,51 см².

По приложению 6 [1] принимаем 2 Ø18 A-III с площадью A_s1 = 5,09 см².

г) Подбор арматуры на отрицательный момент М=21,90 кНм сечение работает как прямоугольное:

По табл.3.1 [1] вычисляем ζ = 0,9478.

Вычисляем площадь сечения растянутой арматуры:

м² = 1,86 см².

По приложению 6 [1] принимаем 2 Ø12 A-III с площадью A_s2 = 2,26 см².

д) Подбор арматуры на первой промежуточной опоре, сечение работает как прямоугольное:

По табл.3.1 [1] вычисляем ζ = 0,832.

Вычисляем площадь сечения растянутой арматуры:

м² = 6,06 см².

По приложению 6 [1] принимаем 8 Ø10 A-III с площадью A_s2 = 6,28 см².

е) Подбор арматуры в средних опорах.

По табл.3.1 [1] вычисляем ζ = 0,853.

Вычисляем площадь сечения растянутой арматуры:

м² = 5,17 см².

По приложению 6 [1] принимаем 8 Ø10 A-III с площадью A_s2 = 6,28 см².

6.4. Расчет прочности наклонных сечений.

Определяем коэффициент f, учитывающий наличие полок тавровых сечений:

Диаметр поперечных стержней устанавливают из условия сварки с продольными стержнями d=20 мм и принимают =5мм класса Вр-I, 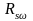=260 МПа. Число каркасов – 2, . Шаг поперечных стержней по конструктивным условиям s=h/2=40/2=20, но не более 15 см принимаем s=15 см. В средней части пролета l/2 шаг s=(3/4)h=30 см.

Влияние свесов сжатой полки:

 0,5 — принимаем _f = 0,095.

Коэффициент _n, учитывающий влияние продольных сил, равен 0, т.к. арматура во второстепенной балке ненапрягаемая.

Тогда коэффициент k:

k = 1 + 0,095 + 0 = 1,095 1,5.

Погонное усилие в поперечных стержнях вычисляем по формуле:

кН/м.

Находим величину Q_bmin:

Q_bmin = _b3·k·R_bt·b·h₀ = 0,6·1,095·0,75·0,9·10³·0,25·0,34  37,7кН.

Проверяем условие:

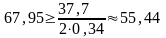, кН/м. – условие выполняется

Определяем максимальны шаг поперечных стержней:

Q_max=83,46 кН

м =35см > s=15 см- условие выполняется.

Вычисляем M_b:

M_b =_b2·k·R_bt·b·h₀²= 2·1,095·0,9·0,75·10³·0,25·0,34² =42,72 кН·м.

кН/м.< кН/м, то расстояние от точки опоры до вершины наклонной трещины определяется по формуле: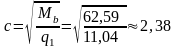 м > м; принимаем с=с_max=1,13.

Вычисляем поперечное усилие, воспринимаемое бетоном сжатой зоны над вершиной наклонного сечения:

кН  Q_bmin = 37,7 кН — условие выполняется.

Поперечная сила в вершине наклонного сечения вычисляется:

Q = Q_max – q₁· c = 83,46 – 11,04· 1,13  70,99 кН.

Вычисляем значение:

м

и проверяем условия: c₀  c = 1,13 м;

c₀ >2h₀ = 2·0,34 = 0,68 м; принимаем с₀=0,68

c₀  h₀ = 0,34 м.

Определяем сумму осевых усилий в поперечных стержнях:

Q_sw = q_sw·c₀ = 67.95·0,68 = 46.21 кН.

Проверяем условие прочности:

Q  Q_b + Q_sw, 70.99 < 37.81+ 46.21 = 84.08 кН- условие выполняется .

Проверка по сжатой наклонной полосе:

Определяем параметр _sw:

Находим коэффициент : .

Проверяем прочность по сжатой полосе между наклонными трещинами. Вычисляем коэффициент _w1, учитывающий влияние поперечных стержней балки:

_w1=1+5_sw = 1+5·7,4·0,00105 = 1,04  1,3.

Находим коэффициент _b1:

_b1 = 1 – ·R_b = 1 – 0,01·8,5·0,9  0,924.

Проверяем условие равновесия:

0,3 _w1 _b1 R_b b h₀ = 0,3·1,04·0,924·8,5·10³·0,25·0,34 = 208,28 кН  Q = 70,99 кН — условие выполняется.

Итак, на приопорных участках устанавливаем арматуру 2Ø5 Вр-I с шагом 150 мм, а в средней части пролета — с шагом 300 мм.