Интегральная кривая распределения .

Таблица 3 (VI.3).

R	Q	ΔQ	ΔQ/Δr
2	16	16	8
4	31	15	7.5
6	44	13	6.5
8	54	10	5
10	63	9	4.5
15	79	16	3.4
20	91	12	2.4
25	97	6	1.2
30	99	2	0.4
35	100	1	0.2
39	100	0	0

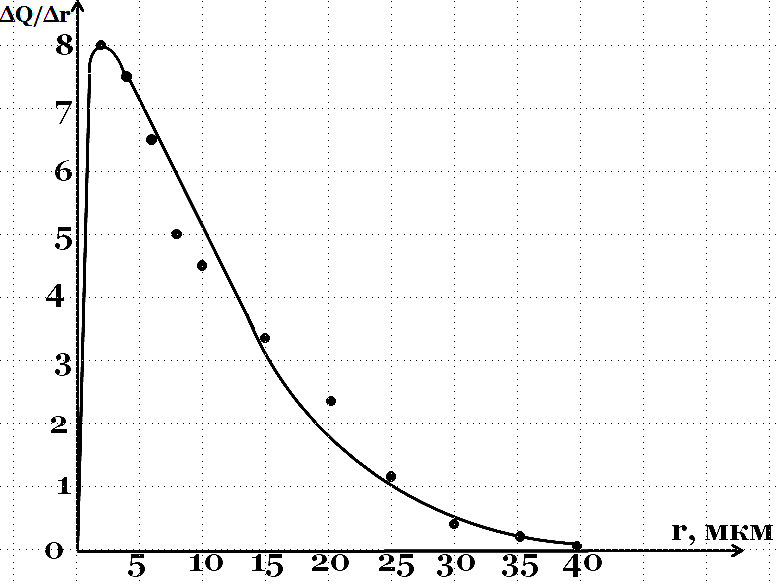
Дифференциальная кривая распределения . Наиболее вероятный размер частиц 2 мкм .

2. Изучение зависимости поверхностного натяжения и адсорбции от концентрации раствора пав методом Ребиндера (максимального давления пузырька).

В этом методе происходит выдувание пузырька воздуха из капилляра в смачивающую его жидкость, при этом давление, необходимое для отрыва пузырьков от кончика капилляра, прямо пропорционально поверхностному натяжению жидкости, удерживающему пузырек. По мере выдувания пузырька это давление возрастает , достигая своего максимального значения ΔP_m в тот момент, когда пузырек примет форму полусферы, т.е.когда радиус его кривизны R станет равным радиусу капилляра r. Это максимальное давление внутри пузырька ΔP_m прямо пропорционально поверхностному натяжению жидкости , и в этом случае применима формула Лапласа в виде :

( VII.38 ) ΔP_m = 2 σ / r .

(Строго говоря, в этой формуле должен присутствовать добавочный член, учитывающий гидростатическое давление столба жидкости, находящегося над пузырьком : h*ρ*g , где h – глубина погружения капилляра в жидкость. Именно для того, чтобы избавиться от него, при практических измерениях стараются сделать так, чтобы кончик капилляра не погружался в жидкость, а только касался её поверхности, тогда можно считать,

что h = 0 ).

Давление внутри пузырька ΔP_m обычно измеряют по разности уровней жидкости в водяном манометре, соединенном с капилляром. Эта разность складывается из суммы подъема и опускания уровня воды в разных коленах манометра от равновесного состояния, причем Δh_m = ΔP_m /(ρ*g) , а формула (VII.38) может быть теперь записана , как : σ = ( Δh_m*ρ*g )*r/2 . Чтобы избежать трудностей, связанных с экспериментальным определением радиуса капилляра r , мы можем принять часть последней формулы за константу капилляра, обозначив её, как K_к = ( ρ*g_*r)/2.

Для определения этой константы производят измерения Δh⁰_m для стандартной жидкости с точно известной величиной поверхностного натяжения σ⁰ при данной температуре, после чего вычисляют константу капилляра по формуле :

(VII.41)

В качестве стандартной жидкости обычно используют дистиллированную воду, для которой величина σ₀ при 20⁰ С равна 72,75 мН/м . Определив константу капилляра К_к , проводят серию измерений растворов с неизвестными значениями поверхностного натяжения и вычисляют их по формуле :

(VII.41a)

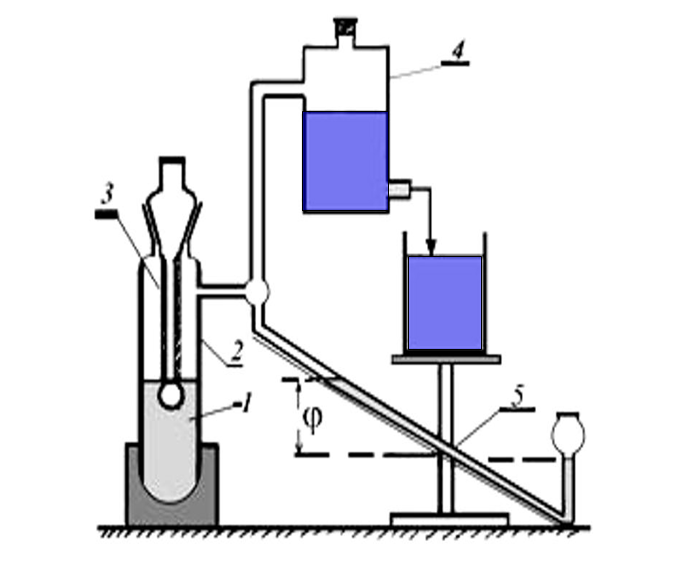
Для выполнения этой работы в лаборатории удобно пользоваться специальным

прибором, разработанным академиком П.А.Ребиндером ( рис. VII.22 ).

Исследуемую жидкость (1) наливают в термостатированный сосудик (2) с боковым отростком, в который опускают капилляр (3). Боковой отросток соединен с устройством для создания разрежения в сосудике

[аспиратором (4) – герметичным стеклянным цилиндром, разрежение воздуха в котором создается за счет вытекающей из него воды ], при этом происходит просасывание воздуха через кончик капилляра в жидкость с образованием пузырьков .

С системой соединен водяной манометр(5), позволяющий определять величины давления в пузырьке по разности уровней воды в обоих коленах манометра (Δh^X =h₁+h₂) .

Перед началом работы тщательно промывают хромовой смесью, обычной водой, а затем дистиллированной водой измерительный капилляр, сосудик и все рабочие колбы. После этого наливают в сосудик 5 –10 мл дистиллированной воды, погружают туда капилляр так, чтобы он только касался поверхности жидкости, но не был погружен в нее. Сосуд помещают в термостат и соединяют с аспиратором, внимательно следя за тем, чтобы уровень воды в аспираторе находился между двумя метками, а в соединительных трубках не было даже капель воды. Скорость вытекания воды из аспиратора регулируют таким образом, чтобы число воздушных пузырьков, проходящих через капилляр, составляло 5 – 8 в минуту. Отсчет показаний манометра производят с помощью увеличительного стекла, фиксируя величину h⁰₁ и h⁰₂ для каждого колена отдельно, и используя в дальнейшем их сумму Δh⁰_m = h⁰₁+h⁰₂. Затем вычисляют константу капилляра К_к по формуле (VII.41), причем проделывают эти измерения не менее пяти раз. Результаты расчетов константы К_к проверяют у преподавателя. После этого приступают к приготовлению исследуемых растворов, которые готовят из исходного раствора ПАВ, полученного у преподавателя, последовательным разведением каждого предыдущего раствора дистиллированной водой в два раза .

В результате получается серия из шести растворов (исходная задача и пять разбавлений) с концентрациями (с₀ ; с₀/2 ; с₀/4;……… с₀/32 ). Дальнейшие измерения проводят таким же образом, как и при вычислении константы капилляра, начиная с самого разбавленного раствора и переходя от меньшей концентрации к большей. Рассчитанные по формуле (VII.41) значения σ_х проверяют у преподавателя по мере нахождения каждого . Закончив измерения серии растворов, получают у лаборанта данные об исследуемом ПАВ (исходная концентрация, молекулярная масса, плотность), после чего строят график зависимости σ от с и заносят данные измерений в протокол работы аналогично приведенному ниже примеру :