2.5 Оформление формул и уравнений

Уравнения и формулы следует выделять из текста в отдельную строку.

Формулы размещают посередине текста. Значения символов и числовых коэффициентов, входящих в формулу, должны быть приведены непосредственно под нею. Значение каждого символа дают с новой строчки в той последовательности, в которой они приведены в формуле. Первая строка расшифровки должна начинаться со слова «где» без двоеточия после него. После формулы, если за ней идет расшифровка символов, ставят запятую, между символом и текстом расшифровки – тире, между элементами расшифровки – точку с запятой. Размерность буквенного обозначения отделяют от текста расшифровки запятой.

Выше и ниже каждой формулы или уравнения должно быть оставлено не менее одной свободной строки.

Условные буквенные обозначения величин должны соответствовать установленным стандартом. В тексте записки перед обозначением параметра дается его пояснение, например: «Временное сопротивление разрыву _в». Прописные и строчные буквы латинского алфавита «О, о» не должны употребляться в обозначениях.

В формулах символы и обозначения должны быть четко написаны в соответствии с правилами правописания, чтобы было ясно, к какому алфавиту принадлежит буква. Не допускается в записке обозначать одинаковыми символами разные понятия, а также разными символами одинаковые понятия. Если несколько величин обозначают одной буквой, то для их отличия необходимо применять индексацию.

Если уравнение не умещается в одну строку, то оно должно быть перенесено после знака равенства (=) или после знаков плюс (+), минус (–), умножения (*), деления (:) или других математических знаков.

Пояснение значений символов и коэффициентов следует приводить непосредственно под формулой в той же последовательности, в которой они даны в формуле. Значение каждого символа и коэффициента следует давать с новой строки. Первую строку пояснения начинают со слова “где” без двоеточия.

Формулы следует нумеровать в пределах всей курсовой работы арабскими цифрами в круглых скобках в крайнем правом положении на строке.

При необходимости допускается нумерация формул в пределах раздела. В этом случае номер формулы состоит из номера раздела и порядкового номера формулы, разделенных точкой, например (2.1).

Допускается выполнение формул и уравнений рукописным способом черными чернилами.

Каждая формула, с включением в нее системы обозначений показателей, отделяется от текста сверху и снизу двумя полуторными интервалами.

Пример. Уровень скидок с цены машиностроительной продукции, поставляемой АПК, для организации ее предпродажного обслуживания определяют по формуле:

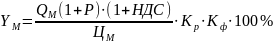, (3.1)

где Y_м – уровень скидки для конкретной машины,%;

Q_м – себестоимость предпродажного и гарантийного обслуживания машины, р;

Р – рентабельность предприятия, %;

НДС – налог на добавленную стоимость, 20%;

К_р, К_ф – поправочные коэффициенты на организацию сервиса на региональном и федеральном уровнях(Кр = 1,3; Кф = 1,2);

Ц_м – цена машины, тыс.руб.

Ссылки в тексте на номер формулы дают в скобках, например: «...в формуле (1.1)».