Программирование арифметических формул.

Приведём теперь пример вычисления по формуле:

или

(назначения вспомогательных величин y1, y2, y3, y4, y5 здесь вполне очевидны).

Исходные величины: х, а, с, r здесь считаются заданными; их значения могут быть произвольными.

Запрограммируем эту формулу в 3-х вычислительных средах: Excel, VBA и MathCAD

1. Программирование формулы в Excel

Как обычно, для исходных данных х, а, с, r отведём ячейки, расположенные в верхнем левом углу рабочего листа.

Правее исходных данных будут находиться формулы для вычисления y1, y2, y3, y4, y5, у

Отметим, что в Excel исходные данные, промежуточные и окончательные результаты могут находиться в произвольных ячейках.

Например, исходные данные могут находиться после (ниже и правее) формул, и при этом все вычисления будут выполняться нормально.

Но лучше всё же придерживаться определённой системы расположения всех величин, помещая исходные данные в левый верхний угол (в «начало») рабочего листа.

Фрагмент рабочего листа для наших вычислений приведён ниже, на Рис. 1:

Рис.1. Фрагмент, который может служить образцом оформления ЭТ для распечатки.

Здесь правее столбца D (в надписи, взятой из панели Рисование) приведены формулы, которые находятся в ячейках D1:D6.

Эти формулы, если начинать их с символа "

можно записывать и в ячейки ЭТ. Например, можно записать в двух соседних ячейках и вычисленный результат и саму формулу: 222,3333333 "=222+1/3

Напомним, что для перехода в режим формул и обратно достаточно нажимать клавиши

Ctrl+ `

(символ ` - «обратный апостроф» - находится под клавишей Esc).

Для того, чтобы дать активной ячейке имя, достаточно щёлкнуть по полю имени (левее строки формул) и прописать это имя в соответствии с общими правилами записи имён.

Оно будет уникальным не только для данного рабочего листа, но и для всей рабочей книги.

Другими словами, данное пользовательское имя может иметь только одна ячейка во всей рабочей книге.

Остальные операции над именами можно осуществлять через

Вставка/Имя /

Сделаем теперь дополнительные пояснения относительно имён ячеек. Без всяких проблем мы дали естественные имена х и а ячейкам В1 и В2 соответственно. Однако, остальные имена несколько отличаются от естественных. Именно, вместо имён с и r мы дали имена сс и rr, так как ввод имени с просто выделяет текущий столбец, а ввод имени r выделяет текущую строку: (column - столбец, row – строка). Далее, имена y1, y2, y3, y4, y5 закреплены за соответствующими ячейками столбца у, поэтому ячейкам D1, D2, D3, D4, D5 мы присвоили имена y_1, y_2, y_3, y_4, y_5 соответственно.

Замечание. Разумеется, можно было обойтись (частично или полностью) без именования ячеек.

Например, можно ячейкам D1, D2, D3, D4, D5 не присваивать имена y_1, y_2, y_3, y_4, y_5 , а просто использовать адреса ячеек D1, D2, D3, D4, D5 в заключительном выражении для y.

Можно было бы вообще не присваивать никаких имён ячейкам. Но это заметно снизило бы наглядность ВД.

Запрограммируем теперь для вычисления по формуле (1) соответствующую пользовательскую функцию в VBA с использованием только операторов присваивания:

Public Function f_4(x, a, c, r)

y1 = (Sin(x)) ^ 3 - (c ^ (1 / 3)) ‘ *

y2 = 2 * Application.Asin(x / 12)

y3 = Log(5 * x) / Log(3) + r ^ (1 / 2)

y4 = (7.54 / (a + 7)) + Abs(x - 5)

y5 = Cos(2 * x) / Sin(2 * x)

f_4 = (y1 / y2) - ((y3 / y4) * y5)

End Function

Этот вариант имеет определённый недостаток.

Именно, в операторе с комментарием ‘ * при c<0 вычисления происходить не будут (почему?). Поэтому можно воспользоваться соответствующей функцией Excel с именем Power, записав этот оператор в виде:

y1 = (Sin(x)) ^ 3 - Application.Power (c , (1 / 3)) ‘ *

(Как отмечалось ранее, в Excel корни нечётной степени из отрицательных чисел извлекаются нормально.)

Программирование формулы (1) в MathCAD.

С помощью операторов присваивания задаём начальные значения переменных с именами x, a, c, r:

С помощью операторов вывода проводим проверку:

Проведём вычисления по формуле (1) пятью разными способами:

1-й способ - с помощью оператора вывода:

2-й способ - с помощью одного оператора присваивания:

При этом вычисленное значение переменной у можно использовать в дальнейших вычислениях.

Поэтому 2-й способ существенно лучше 1-го.

Очевидными достоинствами 1-го и 2 -го способов является их высокая наглядность. Однако, если выражение слишком сложное, то его лучше всё же разделить на несколько более простых.

3-й способ - с помощью нескольких операторов присваивания, когда одно сложное выражение разбивается на несколько простых:

Здесь отслеживаются все промежуточные результаты вычислений. Кроме того, исходное выражение может содержать повторяющиеся подвыражения. В этом случае такое разбиение даёт существенный дополнительный эффект.

Когда используется несколько операторов, можно использовать программный блок (ПБ).

4-й способ - с помощью ПБ:

Можно сказать, что ПБ расположен в "своём" левом верхнем углу.

Значением ПБ является последнее (самое нижнее) выражение блока.

Достоинством ПБ является то, что в одно целое можно объединить большую цепочку вычислений. Кроме того, все промежуточные обозначения являются локальными, то есть, они распространяются только на данный ПБ. А это имеет определённые достоинства. Можно, например, спокойно использовать в ПБ произвольные обозначения, не опасаясь того, что они пересекутся с уже имеющимися.

В то же время, значения промежуточных переменных в ПБ нельзя увидеть и, следовательно, использовать.

Иллюстративный пример:

5-й способ - на базе пользовательской функции с помощью ПБ:

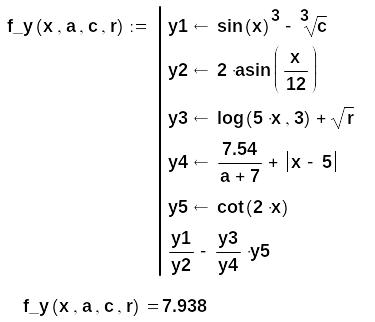
В этом операторе вывода функция

содержит фактические аргументы

Во многих случаях, особенно когда приходится исследовать зависимости выходных величин от одного или нескольких параметров,

5-й способ является наиболее эффективным.

Зафиксируем все аргументы, кроме а и с и построим график функции 2-х переменных: