8. Понятие пользовательской функции

Задание пользовательской функции. Пользовательские функции (ПФ) занимают одно из центральных мест в вычислительной подготовке. Без них невозможно решение многих задач. Понятие это непростое, поэтому начнём с простейших примеров, взяв за основу MathCAD.

Пример 1. Пусть имеется математическая область вида:

f(x) := 2x + 10 (1)

В этой области задана пользовательская функция с именем f.

В записи (1) фигурирует знак присваивания, однако никаких вычислений здесь не происходит. Просто в оперативной памяти формируется подпрограмма, задающая функцию f(x), а х воспринимается здесь как формальный аргумент (или формальный параметр).

Отметим, что в (1) мы могли вместо имени х написать любое другое имя: хх, z5, формальный_аргумент и т.д., и при этом была бы задана одна и та же функция.

Формальный аргумент – это просто произвольное имя. Но, как было сказано ранее, имена в качественном ВД должны в максимальной степени соответствовать обозначениям в исходной задаче.

Итак, (1) задаёт новую функцию, которая будет храниться в памяти и может быть использована в любой момент времени наряду со всеми другими функциями ВС.

Для проверки работы функции f(x) напишем оператор числового вывода:

f(7) = 24 (2)

При выполнении этого оператора вычисляется значение АВ в левой части и правее знака вывода (=) появляется результат вычислений. В нашем случае АВ – это просто указатель функции: f(7).

При вычислении значения f(7) запускается сформированная ранее подпрограмма для вычисления f(x), где вместо х подставляется число 7. В результате работы этой подпрограммы вычисляется значение выражения 27 +10 и полученный результат (число 24) появляется в области (2).

При этом в записи f(7) число 7 называется фактическим аргументом.

В общем случае в качестве фактического аргумента можно использовать произвольное арифметическое выражение.

То есть, можно написать в каком-либо АВ указатель функции вида f(АВ_аргум), где АВ_аргум - произвольное допустимое арифметическое выражение, не содержащее самой функции f. При вычислении f(АВ_аргум), сначала вычисляется Значение_АВ_аргум, затем это значение подставляется вместо формального аргумента х в (1) и на месте f(АВ_аргум) появляется вычисленное значение функции

f(Значение_АВ_аргум).

Пример 2. Пусть, наряду с заданием f(x), имеется оператор присваивания

х := 7

"х полагается равным 7" - это обычный оператор присваивания, при выполнении которого скалярная переменная с именем х (икс) получает значение, равное семи (в ячейку для переменной х заносится число 7).

Этот оператор может быть расположен либо перед, либо после задания нашей функции f(x).

В итоге на данный момент у нас фигурирует два одинаковых имени х: имя обычной переменной и имя формального аргумента функции f(x). Такая ситуация является очень распространённой, и в ней нужно хорошо ориентироваться.

После задания функции f(x) и значения переменной х=7 можно написать оператор вывода:

f(x) = 24

Вычисление значения f(x) здесь происходит по аналогии с вычислением f(7).

В записи f(x) под х понимается фактический аргумент - обычная переменная, значение которой (число 7) задано ранее.

В выражении для функции, наряду с формальным аргументом, могут присутствовать и другие переменные, значения которых заданы и даже произвольные арифметические выражения, значения которых можно вычислить.

Пример 3. Пусть имеется следующий фрагмент ВД:

a:=2 b:=10 f1(x) := ax + b f1(7) = 24

Здесь в выражении для f1(x), кроме формального аргумента х, присутствуют две переменные (a и b), значения которых заданы ранее. Если бы эти переменные не имели никаких значений, они были бы выделены красным цветом, и функция не была бы определена.

Пример 4. (гораздо более сложный и важный, чем 3 предыдущие) Пусть задана функция 3-х аргументов c именем f3:

f3(x, a, b):= ax + b (3)

Здесь мы имеем дело с функцией нескольких аргументов. При вычислении значения этой функции вместо формальных аргументов x, a, b нужно подставить соответствующие фактические аргументы, каждый из которых может быть произвольным АВ.

Например,

f3(7, 2, 10) = 24 f3(2, 7, 10) = 24 f3(10, 2, 7)=27

Если заданы значения переменных x, a, b, например,

a=2 b=10 x=7, то в качестве фактических аргументов можно брать любые АВ, содержащие эти и другие переменные, имеющие определённые числовые значения. При этом сначала вычисляются числовые значения 1-го, 2-го и 3-го аргумента, после чего эти значения подставляются на место формальных аргументов (соответственно, на место x, a, b), затем вычисляется значение функции по формуле (3).

Как известно, АВ могут быть достаточно сложными. Соответственно, и указатель нашей функции может иметь непростой вид. Например, этот указатель можно задать в виде:

f3(sin(ax + b), tan(sin(x-b)), ax + b) (4)

При вычислении значения этой функции сначала будут вычислены значения всех трёх фактических аргументов при a=2 b=10 x=7, а затем эти значения будут подставлены на место соответствующих формальных аргументов и вычислено значение функции. Проверим это, проведя вычисления в двух вариантах:

Два варианта вычисления значения функции

1-й вариант - с предварительным вычислением значений аргументов:

2-й вариант - непосредственное вычисление значения функции:

Точное сравнение полученных значений функции:

Задание для самостоятельной работы. Вычислить без компьютера, а затем проверить в MathCAD, чему равны значения

f3(b, x, a) f3(b-3, x+4, 2x) при a=2 b=10 x=7

Тот, кто разобрался как следует с этой функцией, будет уверенно работать со многими другими пользовательскими (определяемыми) функциями.

На основе функции 3-х переменных, фиксируя 1 или 2 аргумента, можно задавать соответственно функции 2-х или 1-го аргумента.

Например, задав функцию (3) и значения переменных

a=2 b=10 x=7 мы можем задать следующие функции:

1) f3_x(x):= f3(x, a, b) – здесь х – формальный аргумент; a, b – обычные переменные со значениями 2 и 10 соответственно. Функция одной переменной f3_x(x) зависит, кроме основного аргумента х ещё и от 2-х параметров, значения которых фиксированы.

2) f3_x_а(x,а):= f3(x, a, b). Это уже функция двух аргументов: x,а. И ещё эта функция зависит от параметра b.

С учётом того, что параметры можно также считать переменными, ничто не мешает нам иметь весьма гибкий и мощный инструмент для исследования функций многих переменных.

Таким образом, мы задали несколько простейших функций и убедились в правильности их работы. Наиболее универсальной из них является полностью автономная функция f3(x, a, b)

Эта функция, как и другие определённые пользователем функции, может быть использована (в данном ВД) наравне со встроенными функциями СКМ MathCAD.

Таким образом, главный вычислительный инструмент MathCAD- набор функций - может быть неограниченно пополнен пользователем. И это пополнение позволяет существенно увеличить возможности MathCAD.

Кроме того, некоторые встроенные функции MathCAD (например, maximize, minimize) в обязательном порядке требуют задания пользовательских функций. Для построения графика функции двух переменных также необходимо задать соответствующую пользовательскую функцию.

Уровень сложности пользовательских функций может быть произвольным!

Пример 6.

Рассмотрим ситуацию, когда в выражении для функции встречаются встроенные функции и даже повторяющееся подвыражение:

Здесь, для более рациональной записи f(x) целесообразно задать вспомогательную функцию:

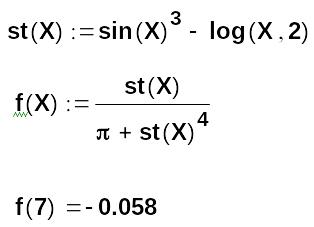
Проведём краткий анализ выражения для функции st(X). Здесь для записи логарифма по основанию 2 использована функция 2 –х аргументов log (X, 2) (аналогичная функция имеется в Excel).

Запись sin(X)³ не содержит ошибок, так как функция является первичным объектом АВ и её значение вычисляется в самую первую очередь (это операция высшего ранга!).

Однако, вполне приемлемой является и запись вида (sin(X))³ , смысл которой уже не вызывает никаких сомнений.

Отметим также, что задавать функции, которые содержат "внутри себя" другие пользовательские функции иногда приходится при самой постановке задачи. Такие задачи встречаются, например, в строительной механике.