Дополнение 1. Понятие невязки приближённого решения.

Понятие невязки (residual) приближённого решения и её связь с погрешностью этого решения.

Погрешность приближённого решения –

это разность между этим решением и точным решением задачи.

Это определение является понятным и естественным, оно применимо к любой задаче. Однако, вычисление погрешности приближённого решения в реальных задачах практически невозможно.

Вся трудность здесь в том, что точное решение, как правило, неизвестно (оно может быть известно только при отладке или тестировании, когда решается задача с заранее известным ответом). Следовательно, неизвестной будет и погрешность приближённого решения.

Погрешность приближённого решения

в реальных задачах неизвестна!

Понятие невязки тоже очень простое, и оно может быть сформулировано следующим образом.

Пусть имеется какое-либо уравнение (или система уравнений).

Пусть найдено тем или иным способом приближённое решение этого уравнения (или системы уравнений).

Невязкой приближённого решения называется разность между левой и правой частями уравнения (или системы уравнений), если вместо неизвестной величины подставить приближённое решение.

Очевидно, такая разность может быть вычислена всегда. Поэтому, можно считать, что невязка приближённого решения в реальных задачах может быть (и должна быть!) вычислена практически всегда. Как, правило, это единственный способ получить представление о погрешности приближённого решения.

При решении одного уравнения невязка является числом, при решении системы уравнений невязка является вектором. Как мы увидим далее, (и это интуитивно понятно!), чем меньше модуль невязки, тем меньше модуль погрешности приближённого решения.

Отметим, что если решается одно уравнение с одним неизвестным, то модуль невязки – это просто абсолютная величина разности между левой и правой частями уравнения после подстановки в уравнение приближённого решения вместо неизвестного.

Если же решается система уравнений, то модуль невязки – это модуль разности между левой и правой частями системы уравнений после подстановки в эту систему приближённого решения вместо неизвестного.

Отметим, что модуль вектора с вещественными элементами – это корень квадратный из суммы квадратов его элементов. Если же элементы вектора – комплексные числа, то модуль вектора - это корень квадратный из суммы квадратов его элементов.

(Модуль вектора называют также его длиной или нормой.)

Далее рассматриваются скалярные уравнения вида f(x)=C с известными точными решениями. Для отыскания невязки приближённого решения такого уравнения достаточно вычислить значение - С. Если же С=0, то есть, решается уравнение вида f(x)=0, то невязка – это просто значение . Отметим здесь же, что любое уравнение вида r(x)=s(x) эквивалентно уравнению f(x)=0, если принять, что f(x)=r(x)-s(x).

На следующих двух иллюстративных примерах рассматривается взаимосвязь между невязками и погрешностями приближённых решений одного уравнения с одним неизвестным.

Пример 1. Уравнение х³ = 8 с известным решением х=2

Возьмём приближённое решение, равное 2.1, найдём для него невязку и сравним её с погрешностью, равной 2.1 - 2 = 0.1

Невязка приближённого решения здесь равна 2.1³- 8= 1.261

Отношение невязки к погрешности здесь будет равно 1.261/0.1=12.61

То есть, невязка больше погрешности почти в 13 раз.

Чтобы проследить за тем, как меняется это соотношение при уменьшении погрешности приближённого решения, проведём следующие вычисления с использованием векторов.

Здесь vPribl – это вектор приближённых решений,

vPogr – это вектор погрешностей приближённых решений,

vNevjazok - это вектор невязок приближённых решений.

Вычислим теперь, во сколько раз невязки приближённых решений больше погрешностей приближённых решений. Для этого запишем отношение двух векторов с использование знака векторизации, что позволит выполнить поэлементное деление:

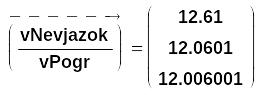
Мы видим, что с уменьшением погрешности приближённого решения отношение невязки этого решения к его погрешности стремится к числу 12. Это число равно значению производной функции f(x)=x³ в точке х=2. Можно доказать, что такой факт имеет место для произвольной функции f(x)! Мы видим, далее, что с уменьшением погрешности уменьшается и невязка приближённого решения. Но для нас здесь важно другое – то, что с уменьшением невязки уменьшается погрешность приближённого решения. (Напомним, что нам всегда известна невязка, но неизвестна погрешность приближённого решения.)

Более того, мы можем сделать следующее заключение.

После вычисления невязки можно получить приближённое значение погрешности приближённого решения, поделив эту невязку на производную функции в точке приближённого решения.

Проверим это на нашем примере, сразу используя векторную запись:

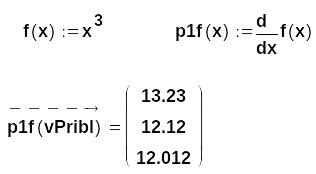
Очевидно, данный приём даёт положительный эффект!

Итак, для приближённого отыскания погрешности приближённого решения достаточно поделить невязку этого решения на значение производной в точке приближённого решения.

Это заключение можно получить из достаточно известной формулы:

если х1  х0, то f(x1)-f(x0)  f '(x1)(х1-х0) (*)

Если принять за х0 точное, а за х1 – приближённое решение, то, учитывая, что f(x0)=0, мы получим из (*) приближённое равенство:

x0  x1 – f(x1) / f '(x1) (**)

Задание. Самостоятельно вычислить х0 по формуле (**) для разных значений х1:

х1=2.1 х1=2.01 х1=2.001

и сделать соответствующие выводы.

Итак, в нашем примере невязка существенно превосходит погрешность приближённого решения.

Пример 2. Другое уравнение с известным решением х=2:

Общие выводы.

1. В зависимости от конкретной задачи, невязка приближённого решения может быть либо значительно меньше, либо значительно больше погрешности этого приближённого решения.

2. Во всех случаях, чем меньше невязка приближённого решения, тем меньше его погрешность. Но из малости невязки (которую всегда можно вычислить), вообще говоря, ещё не следует малость погрешности приближённого решения.

А эта погрешность в реальных задачах практически всегда остаётся неизвестной. Почему?

Аналогичные выводы можно сделать и в отношении систем уравнений! Однако, как правило, если невязка приближённого решения достаточно мала, например, имеет порядок 10^-13, то, если даже погрешность этого решения будет в 1000 раз больше невязки, эта погрешность будет иметь порядок 10^-10, то есть, погрешность приближённого решения также будет достаточно мала!

Итак, на практике можно (с определёнными оговорками) всё же считать, что если мала невязка, то, как правило,

мала и погрешность приближённого решения.

После отыскания приближённого решения любых уравнений и систем необходимо вычислить соответствующую невязку и проанализировать её.

В заключение рассмотрим очень интересный пример неправильного решения простого уравнения х⁷=0 в MathCAD.

Точным решением этого уравнения является значение х=0 – это знает и школьник. Однако, MathCAD этого знать не может: он просто решает поставленную задачу по определённым алгоритмам. Приняв в качестве начального приближения х=0.1, получим решение с помощью функции root:

Мы видим, что искомое решение просто осталось равным начальному приближению, а использование функции root не дало никакого эффекта.

Если вместо функции root использовать Given/Find или надстройку «Поиск решения» в Excel, мы получим тот же результат, что и с функцией root! Связано это с тем, что достижение точности при вычислениях во всех этих случаях определяется по величине невязки приближённого решения. В нашем случае для начального приближения х=0.1 эта невязка равна 0.1⁷=10^-7, то есть достаточно мала!

Задание. Решить уравнение х⁷=0 с начальным приближением х=0.1 через вычислительный блок Given/Find в MathCAD и через надстройку «Поиск решения» в Excel.