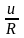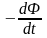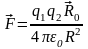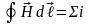- •Методические указания к решению задач по расчету простых и сложных электрических цепей постоянного тока
- •Примеры
- •Решение
- •Методические указания по расчету линейных электрических цепей синусоидального тока
- •Решение
- •Литература
- •Единицы электрических и магнитных величин
- •Элементарная математика
- •Комплексные числа
- •Действия над комплексными числами
- •Основные законы электротехники
- •Основные формулы и уравнения электротехники
- •Соотношения между током и напряжением на элементах электрической цепи
- •Приложение д Методика использования калькуляторов для выполнения расчетов с комплексными числами
Элементарная математика
1. Умножение многочленов
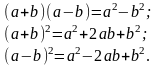
2. Действия с дробями
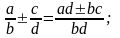
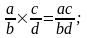
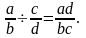
3. Пропорция
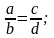
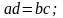
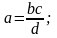
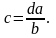
4. Действия со степенями и корнями
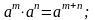
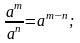
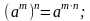
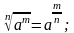
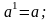
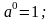
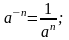
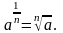
5. Действия с нулем и бесконечностью
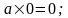
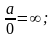
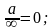
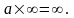
6. Неопределенности
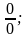
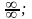
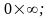

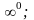
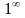 .
.
7 .
Прямоугольный треугольник
.
Прямоугольный треугольник
Теорема Пифагора
β
с
a
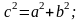
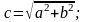
b
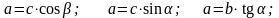
а
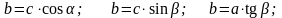
Рисунок 22
8. Формулы тригонометрии
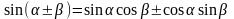 ;
;
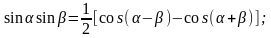
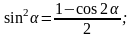
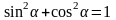 .
.
9. Раскрытие определителя третьего порядка:
а) по элементам строки или столбца:
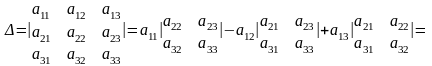
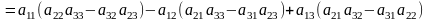 ;
;
б) по правилу треугольников:
«+» «-»



 а11
а12
а13
а11
а12
а13
а11
а12
а13
а11
а12
а13
D = а21 а22 а23 + а21 а22 а23
а31 а32 а33 а31 а32 а33
в) приписыванием двух первых столбцов справа:
+ + +
а11 а12 а13 а11 а12
D
=  а21
а22
а23
а21
а22
а21
а22
а23
а21
а22
а31 а32 а33 а31 а32
- - -
Комплексные числа
Комплексное
число, соответствующее точке, в которой
лежит конец вектора
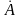 (рисунок 23), может быть записано в
следующих формах:
(рисунок 23), может быть записано в
следующих формах:

Рисунок 23
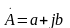 —
алгебраической;
—
алгебраической;
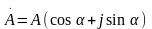 — тригонометрической;
— тригонометрической;
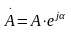 — показательной;
— показательной;
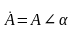 — полярной.
— полярной.
Здесь
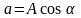 — действительная
часть комплексного числа, А;
— действительная
часть комплексного числа, А;
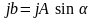 — мнимая
часть комплексного числа;
— мнимая
часть комплексного числа;
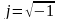 — мнимая
единица;
— мнимая
единица;
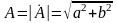 — модуль
комплексного числа;
— модуль
комплексного числа;
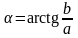 — угол
(или аргумент) комплексного числа.
— угол
(или аргумент) комплексного числа.
Комплексное
число
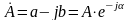 называется сопряженным комплексному
числу
называется сопряженным комплексному
числу
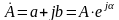 .
Произведение комплексно-сопряженных
чисел — число вещественное, равное
квадрату их модуля:
.
Произведение комплексно-сопряженных
чисел — число вещественное, равное
квадрату их модуля:
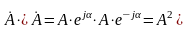 .
.
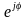 — оператор
поворота на угол φ.
— оператор
поворота на угол φ.
Умножение
комплексного числа
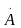 на число
сводится к повороту вектора
в комплексной плоскости на угол φ:
на число
сводится к повороту вектора
в комплексной плоскости на угол φ:
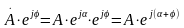 .
.
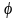 >
0 —
поворот против
часовой стрелки.
>
0 —
поворот против
часовой стрелки.
< 0 — поворот по часовой стрелке.
Действия над комплексными числами
Вычисления
над комплексными числами производятся
так же, как и над обыкновенными двучленами,
полагая
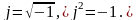
При делении одного комплексного числа на другое, записанных в алгебраической форме, уничтожают мнимость в знаменателе, для чего умножают числитель и знаменатель на число, сопряженное знаменателю:
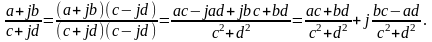
Возведение
в степень:
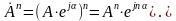
Извлечение
корня:
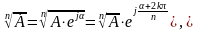
где k — целое число.
Приложение Г
Основные законы электротехники
Закон Ома |
i
=
|
Первый закон Кирхгофа |
∑i = 0 |
Второй закон Кирхгофа |
∑e = ∑u |
Закон Джоуля–Ленца |
p = i2R |
Закон электромагнитной индукции |
e
=
|
Закон Кулона |
|
Закон полного тока |
|