Решение

1. Выбираем произвольно направления токов в ветвях (рисунок 9).

2. Составляем систему уравнений по законам Кирхгофа для определения токов в ветвях.

Так как в схеме 6 ветвей, необходимо составить 6 уравнений: по первому закону Кирхгофа — три уравнения (на единицу меньше числа узлов) и по второму закону Кирхгофа недостающее число уравнений, т.е. также три уравнения.

Система уравнений для расчета токов имеет вид:

(для узла а); (2) (для узла b); (3) (для узла с); (4) (для контура abca); (5) (для контура acda); (6) (для контура bdcd). (7)

В уравнениях (2)–(4) притекающие к узлу токи принимали положительными, оттекающие от узла токи –— отрицательными. В уравнениях (5)–(7) все ЭДС и напряжения, совпадающие с направлением обхода по контуру (по часовой стрелке), записывали положительными, не совпадающие — отрицательными.

Решая полученную систему уравнений (2)–(7), можем найти токи в ветвях.

Рассмотренный метод в большинстве случаев является достаточно громоздким, при большом числе уравнений для решения системы целесообразно применять ЭВМ.

Для упрощения расчета разработаны методы, в основе которых также положены уравнения Кирхгофа, но количество уравнений значительно сокращено.

3. Определяем токи в ветвях методом контурных токов. Считаем, что в каждом независимом контуре схемы (рисунок 9) течет свой контурный ток: I₁₁, I₂₂, I₃₃. Для единообразия контурные токи направляют в одну сторону, в нашем случае по часовой стрелке.

Составляем уравнения по второму закону Кирхгофа относительно контурных токов. Направления обхода контуров примем также по часовой стрелке.

Система уравнений имеет вид:

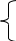
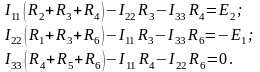
Подставляем известные значения сопротивлений и ЭДС:

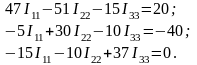(8)

Дальнейший расчет можно вести или методом последовательного исключения неизвестных, или методом определителей. Выбираем последний как более упорядоченный.

Находим главный определитель, используя разложение по элементам столбца:

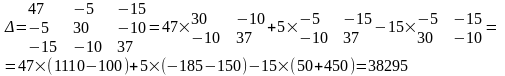
Для нахождения контурного тока I₁₁ заменяем в главном определителе первый столбец на свободные члены системы (8).

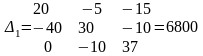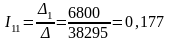; А.

Для контурного тока I₂₂

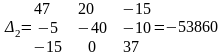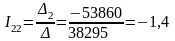; A.

Для контурного тока I₃₃

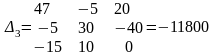; A.

Чтобы убедиться в правильности расчета, подставим найденные контурные токи в первое уравнение системы (8):

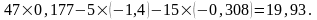
Полученное значение 19,93 ≈ 20 равно правой части первого уравнения системы (8), т.е. система уравнений решена правильно.

Определяем истинные токи в ветвях. Ток в ветви равен алгебраической сумме контурных токов, протекающих в этой же ветви.

Рассчитываем значения токов в ветвях схемы рисунке 9, сравнивая направления контурных токов в ветвях с направлением истинных токов.

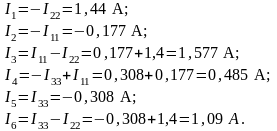
Действительные направления токов I₂ и I₅ противоположны принятым для них на рисунке 9 за положительные.

4. Составляем баланс мощностей.

На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источниками питания.

Уравнение энергетического баланса имеет вид:

.

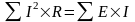Мощность источника энергии EI записывается со знаком плюс, если ток в источнике совпадает с направлением ЭДС. Если же ток противоположен направлению ЭДС, то этот источник ЭДС является потребителем энергии и его мощность записываем со знаком минус.

В нашем случае

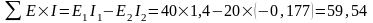Вт.

Мощность тепловых потерь в сопротивлениях

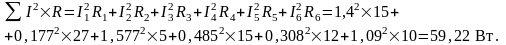
Расхождения в результатах вычислений не превосходят 1%, это означает, что токи рассчитаны правильно.