
- •Сплайны второго порядка.
- •Переменные и структурная схема расчета.
- •С начало труктурная схема расчета.
- •Лабораторная работа №2 Определение изменения давления в пласте при упругом режиме (прямоугольный контур)
- •Основные константы
- •Лабораторная работа №3. Расчет показателей разработки нефтяного месторождения в законтурной области пласта при упругом режиме.
- •Основные константы
- •. Задача теплообмена в трубопроводе нефтеперевозки .
- •Цель срс №2.
- •Методические указания Решение обыкновенных дифференциальных уравнений второго порядка изучалось ранее. Необходимо вспомнить или восстановить ранее пройденный материал. Лабораторная работа №4
- •Алгоритм решения прямой задачи:
- •Самостоятельная работа №3
- •Метод обращения разностной схемы
- •А лгоритм метода обращения разностной схемы:
- •Блок-схема срс 3
- •Лабораторная работа № 5.
- •Блок-схема процедуры ti
- •Блок-схема основной программы
Цель срс №2.
Написать программу для расчета температуры вдоль трубопровода , используя трехточечную разностную схему (приближенное решение);
Изучить влияние длины трубы L, θ1 и θ2 , α и θ0 на распределение температуры;
Следует найти точное решение задачи (4.1)-(4.2). Для этого надо решить дифференциальное решение 2-порядка, считая λ=const. Точное решение надо сравнить с приближенным решением в узлах сетки и найти погрешность метода;
Результаты представить на одном графике для сравнительного анализа.
Методические указания Решение обыкновенных дифференциальных уравнений второго порядка изучалось ранее. Необходимо вспомнить или восстановить ранее пройденный материал. Лабораторная работа №4
Численное решение прямой задачи для уравнения акустики.
Уравнение акустики
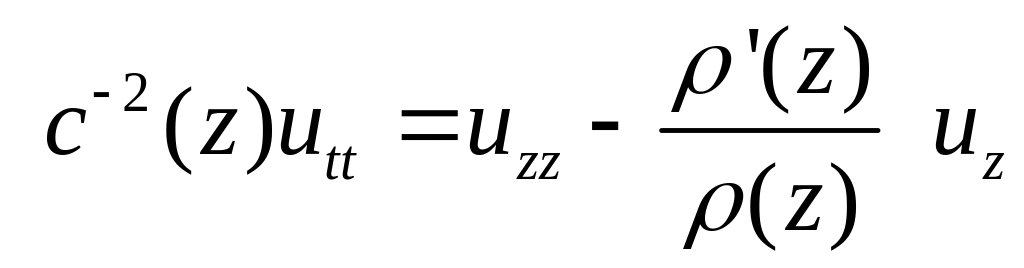
Здесь
![]() - скорость распространения волн,
- скорость распространения волн,
![]() - плотность среды,
- плотность среды,
![]() - акустическое давление, т.е. отклонение
давления от нормального при распространении
акустических колебаний.
- акустическое давление, т.е. отклонение
давления от нормального при распространении
акустических колебаний.
Предположим, что плотность среды и скорость распространения волн известны. Пусть до момента времени t=0 среда находилась в покое, т.е.
u (x,t)=0 при t<0
Предположим, что, начиная с момента времени t=0 на границе z=0 начинает действовать источник акустических колебаний.
![]()
В прямой задаче требуется определить функцию u(z,t) , т.е. смоделировать процесс распространения акустических волн.
Прямую задачу после преобразовании решаем конечно-разностным методом.
Заменяем производные конечно-разностными аналогами:
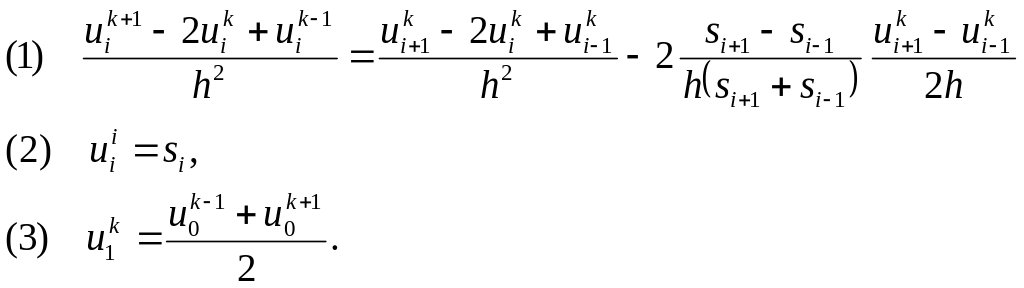
С хему
(1) упростим, сокращая и группируя подобные
слагаемые:
хему
(1) упростим, сокращая и группируя подобные
слагаемые:
![]() .
.
Из (3) находим
![]() .
.
Алгоритм решения прямой задачи:
Находим
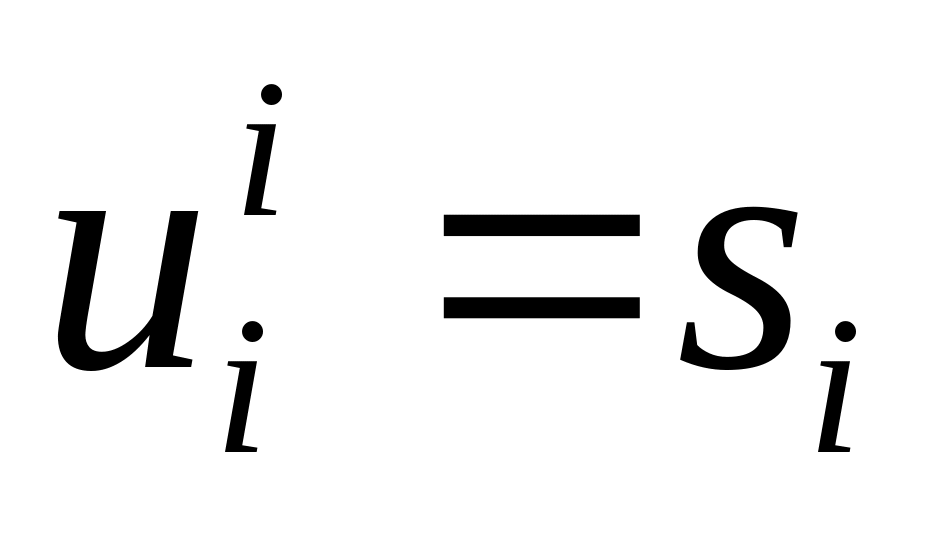 ,
при
,
при
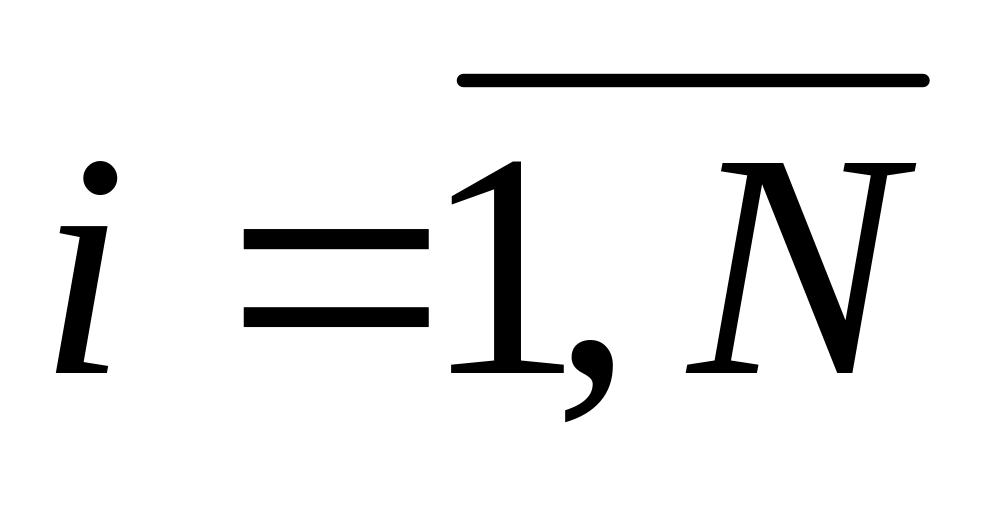 ;
;По формуле (15) определяем
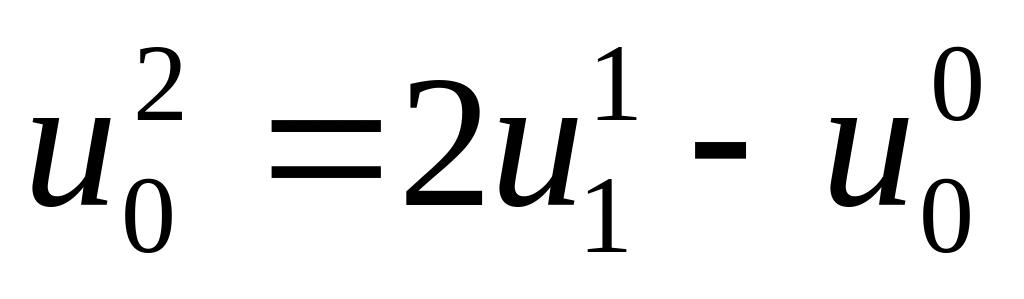 ;
;Из схемы (14) находим
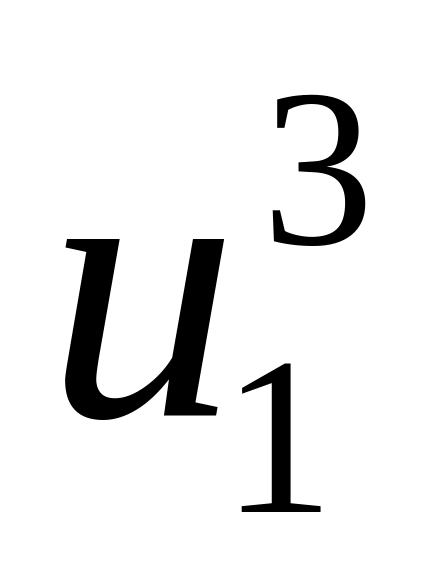 ;
;Из (15) находим
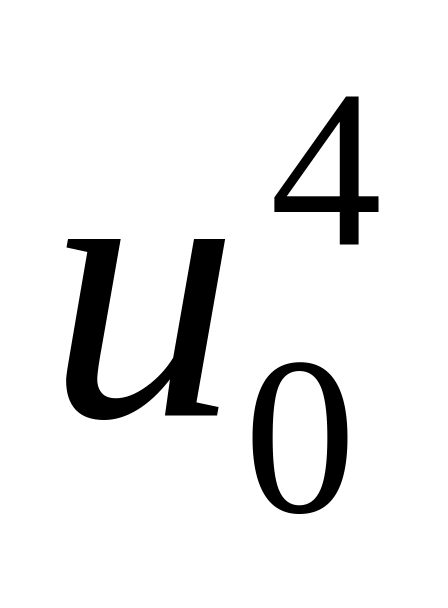 ;
;По формуле (14) определяем
 ;
;По формуле (14) определяем
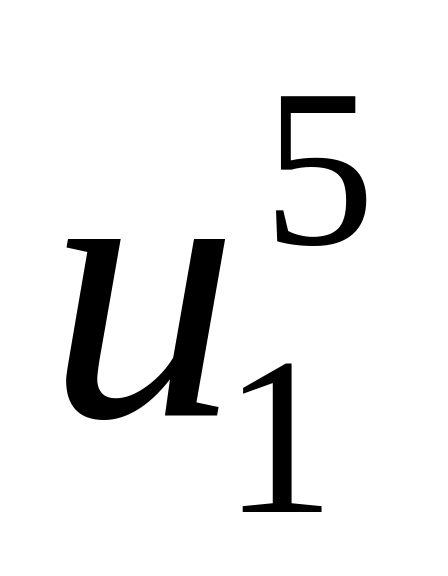 ;
;Из (15) находим
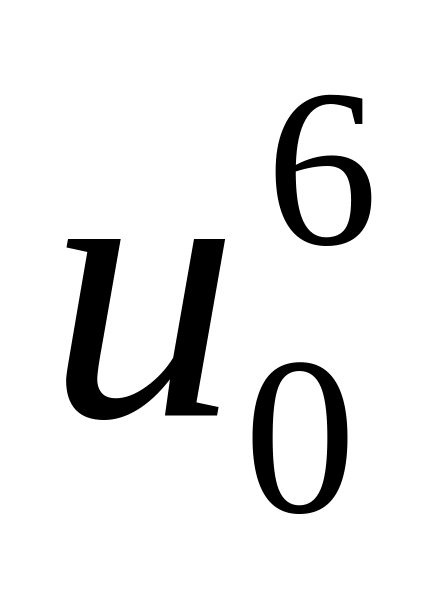 ;
;
и т.д.
Б
u1[0]:=2u0[1]-u0[0]
u1[i]:=2(S((i-1)h)*u0[i+1]+S((i+1)h)*u1[i-1])/ (S((i+1)h)+S((i-1)h))-u0[i]










 лок-схема
лабораторной работы №4
лок-схема
лабораторной работы №4



u0[j]:=u1[j]; вывод
(k,u0[j])



В лабораторной работе №4 надо написать программу численного решения прямой задачи акустики. Результаты представить в виде графиков.
Самостоятельная работа №3
Численное решение обратной задачи для уравнения акустики.
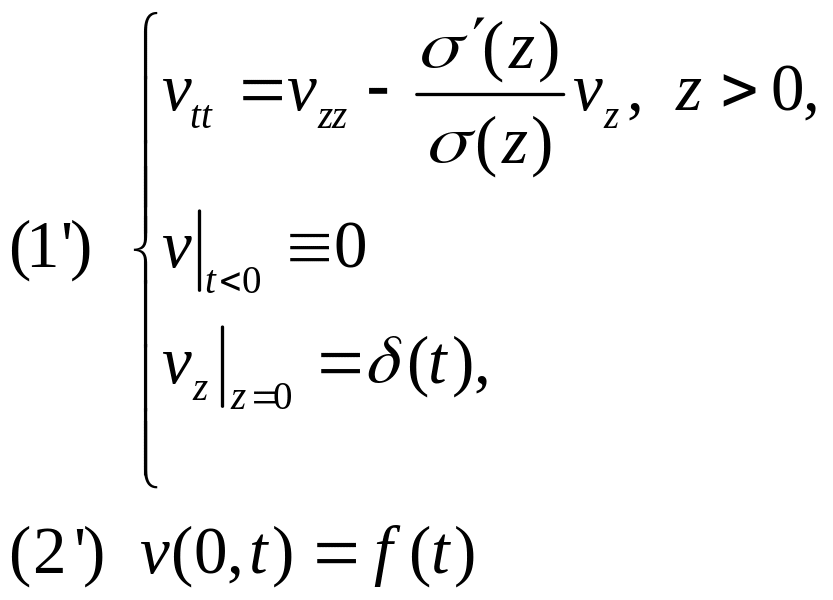
Обратная
задача:
определить коэффициент
![]() по известным данным о решении прямой
задачи
по известным данным о решении прямой
задачи
![]() из (1),
(2).
из (1),
(2).
Условие
![]() означает, что до момента времени
означает, что до момента времени
![]() среда находилась в покое.
среда находилась в покое.
Метод обращения разностной схемы
Основная идея метода обращения разностной схемы – замена обратной задачи конечно-разностным аналогом и дальнейшее решение полученной системы нелинейных алгебраических уравнений достаточно простым способом.
Для численного решения записываем
конечно-разностную апроксимацию обратной задачи :
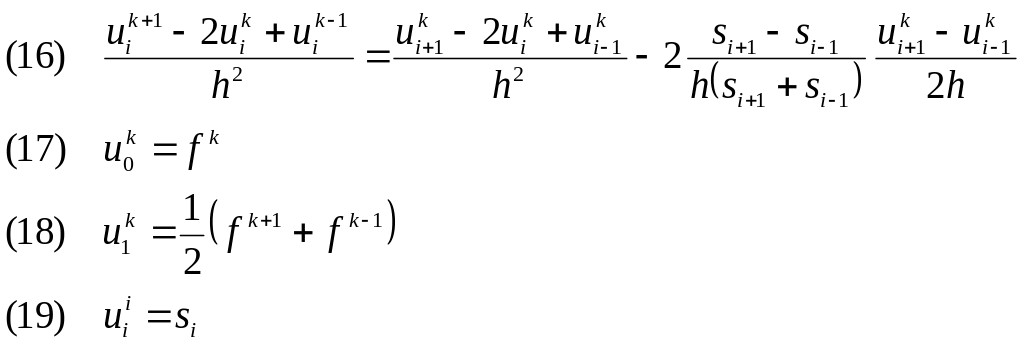
и упрощаем (8)
![]() .
.
Для
нахождения неизвестного коэффициента
![]() на
на
![]() слое полагаем в (20)
слое полагаем в (20)
![]() и получаем уравнение для
.
Откуда находим
из соотношения
и получаем уравнение для
.
Откуда находим
из соотношения
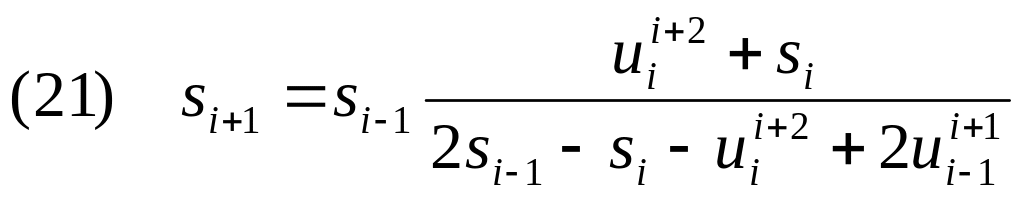 .
.
