
- •Методические указания и примеры решения задач контрольной работы по мпур Графическое решение задачи лп
- •Симплекс-метод решения задачи линейного программирования
- •Динамическое программирование
- •Понятие об игровых моделях.
- •Методы и модели решения игровых задач Принцип минимакса
- •Решения игр в смешанных стратегиях
- •Геометрический метод
- •Исключение доминируемых стратегий
- •Метод линейного программирования
- •Решение игры симплекс-методом
- •Игровые модели в условиях риска
- •Игры с природой
- •Биматричные игры
Игровые модели в условиях риска
Риск определяется возможностью отклонения от желаемого результата в худшую сторону или выхода за пределы допустимого диапазона, интервала, что приводит к нежелательным, негативным последствиям.
Для принятия
решений в условиях риска используют
методы теории вероятностей в сочетании
с другими математическими методами. В
таком случае, факторы, например, состояния
среды представляют собой либо случайные
величины, либо случайные функции. Они
описываются определенными статистическими
характеристиками, например, математическим
ожиданием и дисперсией и обладают
статистической устойчивостью. При этом
производят замену случайных факторов
их средними значениями, математическим
ожиданием и задача становится
детерминированной. Тогда можно применять
и методы линейного программирования,
если по каждому состоянию среды yj
известна вероятность ее проявления pj.
принимающий решение ориентируется на
средние, наиболее вероятные результаты,
однако при этом не исключен риск получения
не того результата, на который была
рассчитана коммерческая стратегия, а
значит и не существует однозначного
соответствия. В таком случае мерой риска
можно считать среднее квадратическое
отклонение. Тогда путем сравнения на
плоскости соответствующих каждому
решению, например, среднего ожидаемого
дохода
![]() и риска
и риска
![]() ,
можно выбрать доминирующие решение.
Однако, если появляются несравнимые
пары
,
можно выбрать доминирующие решение.
Однако, если появляются несравнимые
пары
![]() ,
то образуется, так называемое, множество
оптимальности по Парето, среди которого
и следует искать лучшее решение.
,
то образуется, так называемое, множество
оптимальности по Парето, среди которого
и следует искать лучшее решение.
Случайность исходов игр в условиях риска обуславливается случайным состоянием среды или выбором действий противоположной стороны или определяется вероятностным характером проявления исхода при выбранной хозяйственной стратегии.
Следует заметить, что ситуации, в которых риск связан не с сознательным противодействием противоположной стороны (среды), а с недостаточной осведомленностью о ее поведении или состоянием лица, принимающего решение, называются «играми с природой».
Игры с природой
Пример. Дана таблица выигрышей в игре с природой
-
П1
П2
П3
П4
А1
13
-5
3
8
А2
0
8
14
2
А3
5
4
5
7
Определим оптимальную стратегию первого игрока по различным критериям:
1) по критерию максимального среднего выигрыша, если экспертные оценки вероятностей составляют р1, р2, р3, р4,
где р1=0,1, р2=0,3, р3 =0,4, р4=0,2.
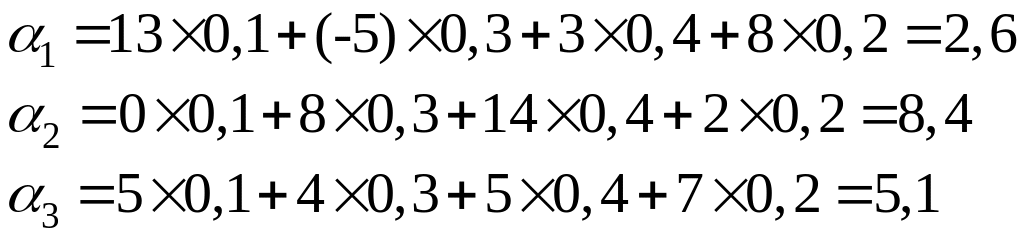
![]()
Следовательно, оптимальной является стратегия А2.
2) по критерию Сэвиджа.
Найдем матрицу
риска. Матрица
риска строится следующим образом. По
каждому столбцу находится элемент с
максимальным значением
![]() .
Каждый элемент матрицы риска в j-том
столбце находится как разность rij
= j
– ij.
Следовательно, матрицу риска R
записываем следующим образом:
.
Каждый элемент матрицы риска в j-том
столбце находится как разность rij
= j
– ij.
Следовательно, матрицу риска R
записываем следующим образом:
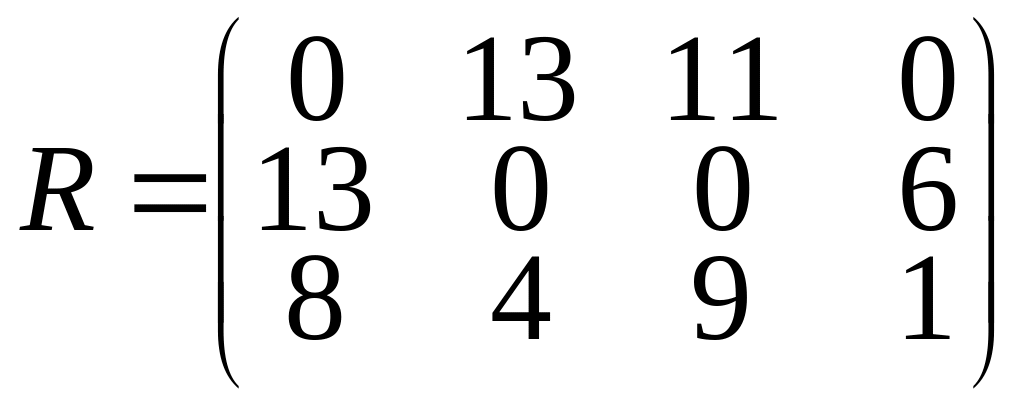
![]() .
.
Оптимальной является третья стратегия А3.
3)
По критерию Гурвица с показателем
пессимизма
![]() .
.
![]()
G1 = (1/4) (-5) + (1 – (1/4)) 13 = 34/4,
G2 = (1/4) 0 + (1 – (1/4)) 14=42/4,
G3 = (1/4) 4 + (1 – (1/4)) 7=25/4,
G=max (34/4, 42/4, 25/4) = 42/4.
Оптимальная стратегия - А2.
4) По критерию Вальда:
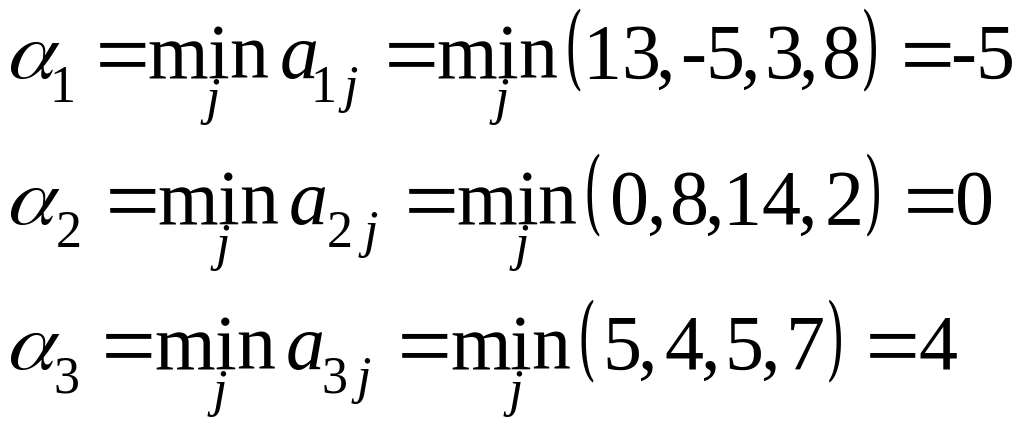
![]() .
.
Оптимальная стратегия - А3.
