Метод линейного программирования

Допустим, что все элементы (выигрыши) платежной матрицы положительны (a_ij  0) (если это не так, то можно ко всем элементам прибавлять достаточно большое число M, сделав их положительными. При этом цена игры увеличится на M, а решение задачи и не изменится). Если все a_ij  0, то  > 0. Пусть платежная матрица не содержит седловой точки, т.е. игра решается в смешанных стратегиях:

.

Применение игроком I оптимальной смешанной стратегии гарантирует ему средний выигрыш, не меньше цены игры , независимо от поведения игрока II. Игрок II, применяя оптимальную смешанную стратегию гарантирует для себя минимальный проигрыш (не больше ).

Если игрок II применяет свою чистую стратегию B_j, а игрок I — свою оптимальную стратегию , то средний выигрыш игрока I равен:

Если игрок I применяет чистую стратегию А_i, а игрок II – свою оптимальную смешанную стратегии , то средний выигрыш игрока II составит

Учитывая, что _j не может быть меньше  для игрока I, а и не может быть больше  для игрока II, двойственную задачу линейного программирования можно записать следующим образом:

1) для игрока I:

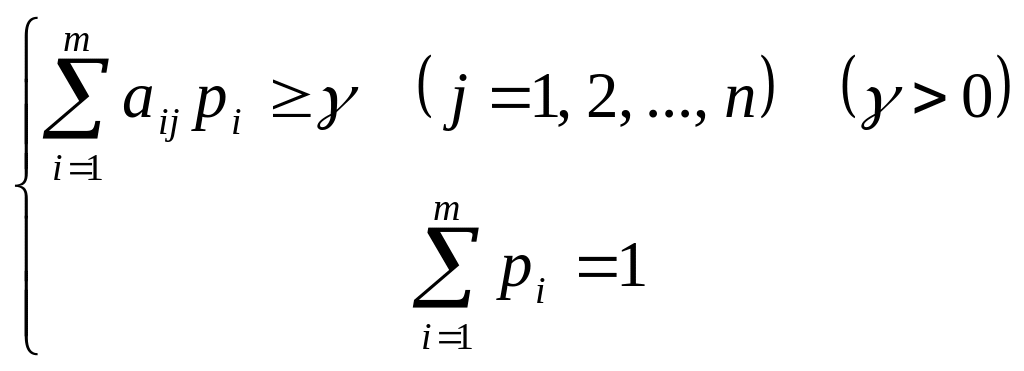
2) для игрока II:

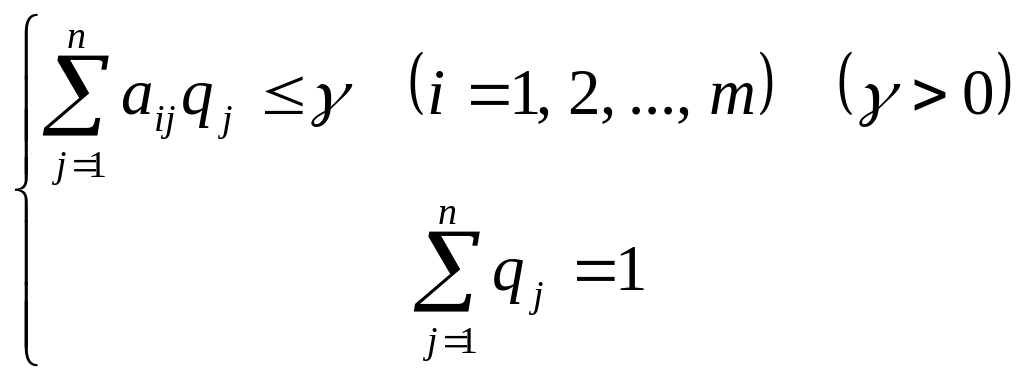
Смысл этих систем уравнений заключается в следующем: игрок I стремится увеличить цену игры (  max), он действует так, чтобы его средний выигрыш при использовании его стратегий с вероятностями p_i для любой j-й стратегии игрока II был не меньше величины , которую он стремится увеличить. Игрок II стремится уменьшить свой проигрыш (  min), т.е. он действует так, чтобы его средний проигрыш при использовании его стратегий с вероятностями q_j при любой i-й стратегии игрока I не превышал величину , которую он стремится уменьшить.

Задача состоит в нахождении двух оптимальных смешанных стратегий и , которые дают для игрока I максимально возможный для него средний выигрыш, а для игрока II минимально возможный для него средний проигрыш.

Разделив левую и правую части неравенств на цену игры  > 0, получим:

Введем обозначения:

Тогда выражения примут следующий вид:

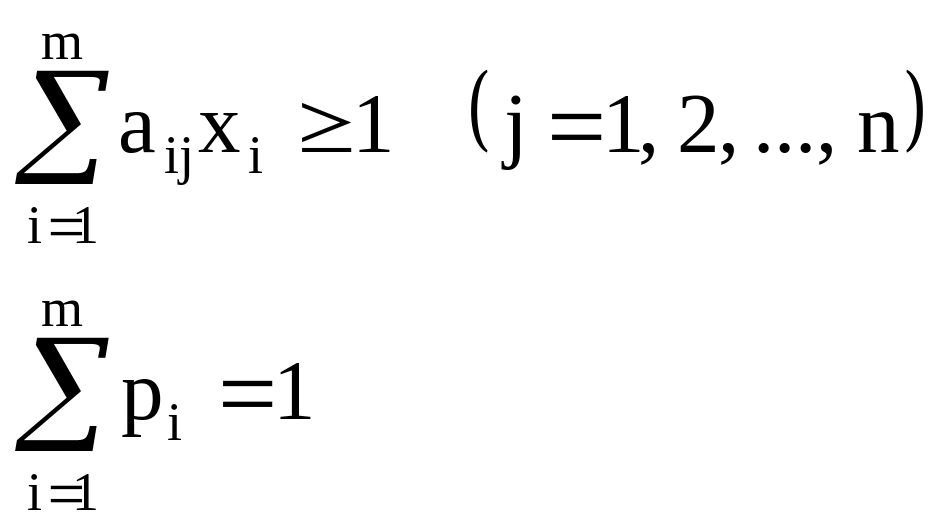
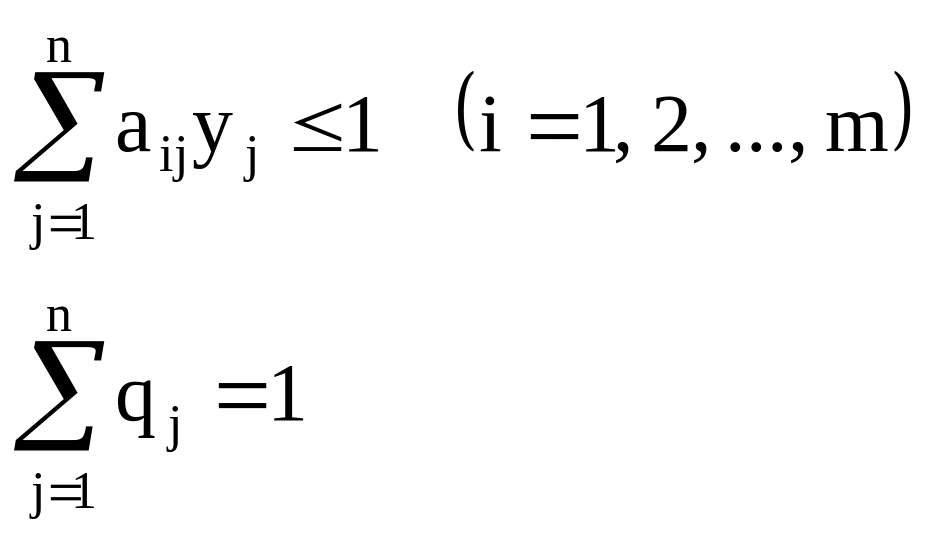
Из равенств и следует, что переменные x_i и y_j должны удовлетворяют условиям:

Учитывая, что игрок I стремится максимизировать , а игрок II стремится минимизировать , переменные x_i и y_j должны быть выбраны так, чтобы целевая функция достигала минимума, а целевая функция достигала максимума.

Таким образом, задача решения игры сводится к задаче линейного программирования. Оптимальные стратегии и игры с платежной матрицей А могут быть найдены путем решения симметричной пары двойственных задач линейного программирования:

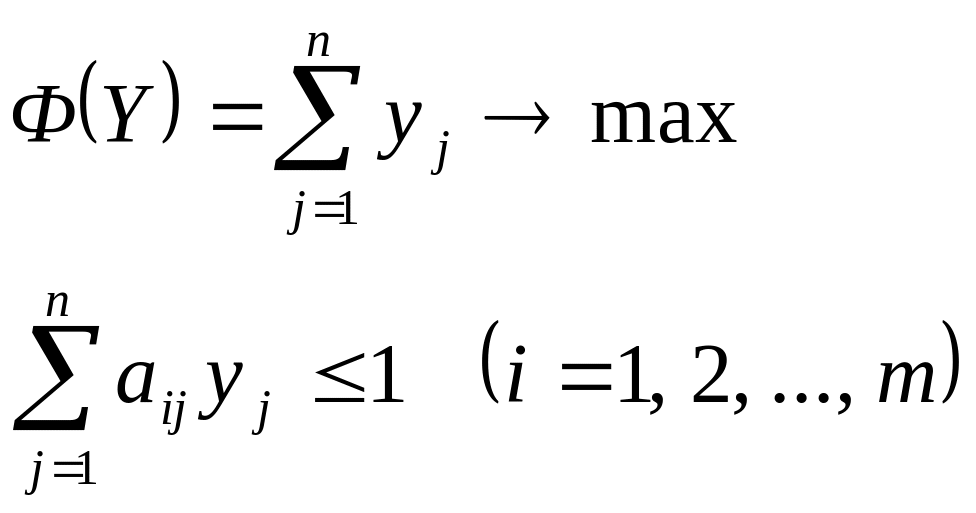
Решая их, находим x_i, y_j, цену игры  и оптимальные стратегии и .

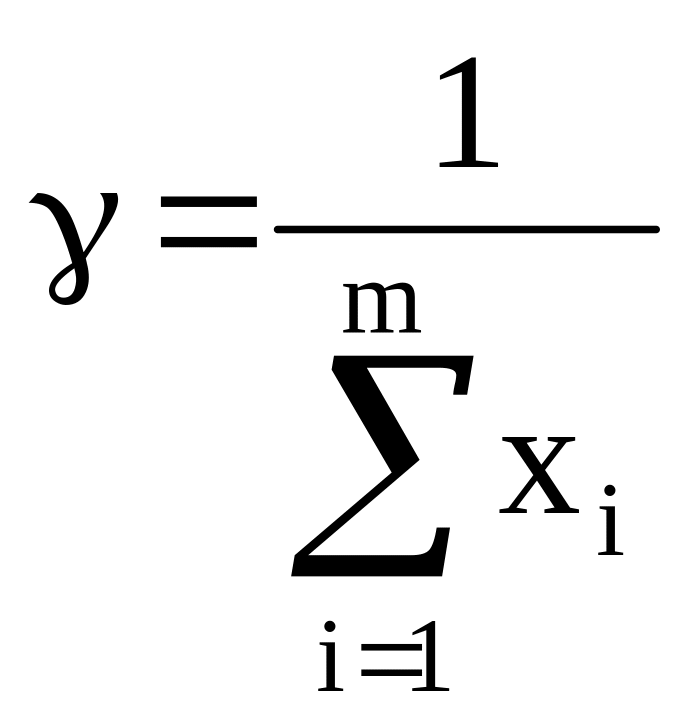или

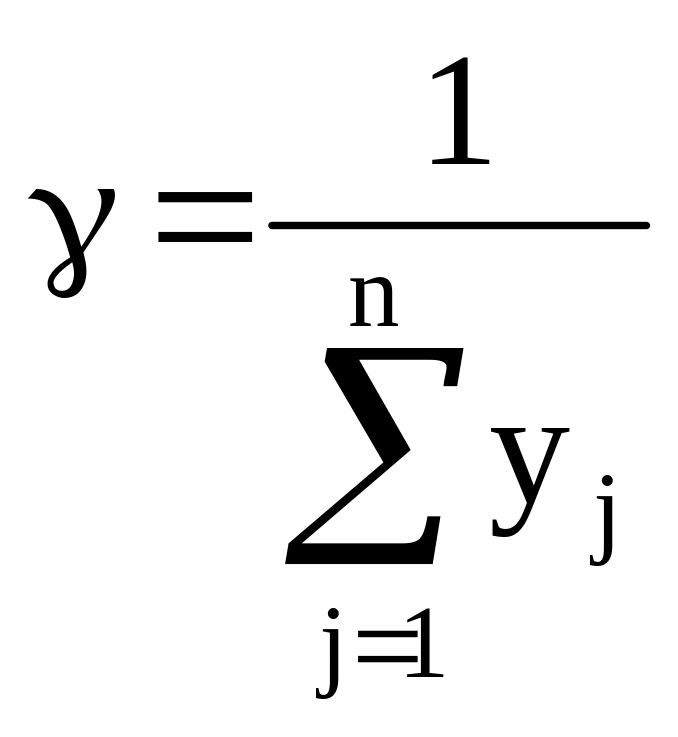
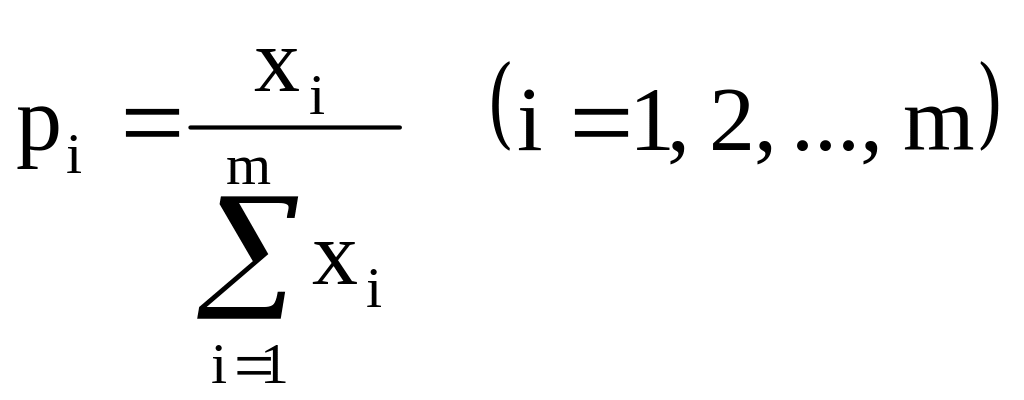
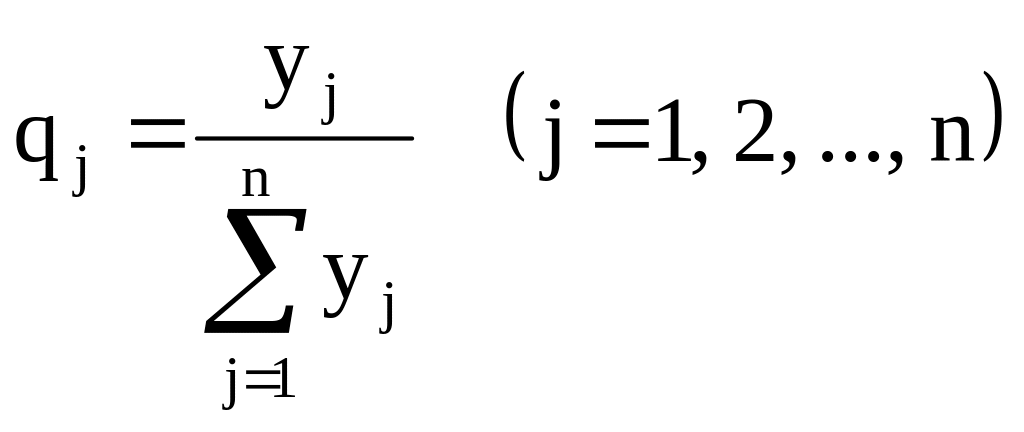
Решение игры симплекс-методом

Пример. Найти решение матричной игры с платежной матрицей:

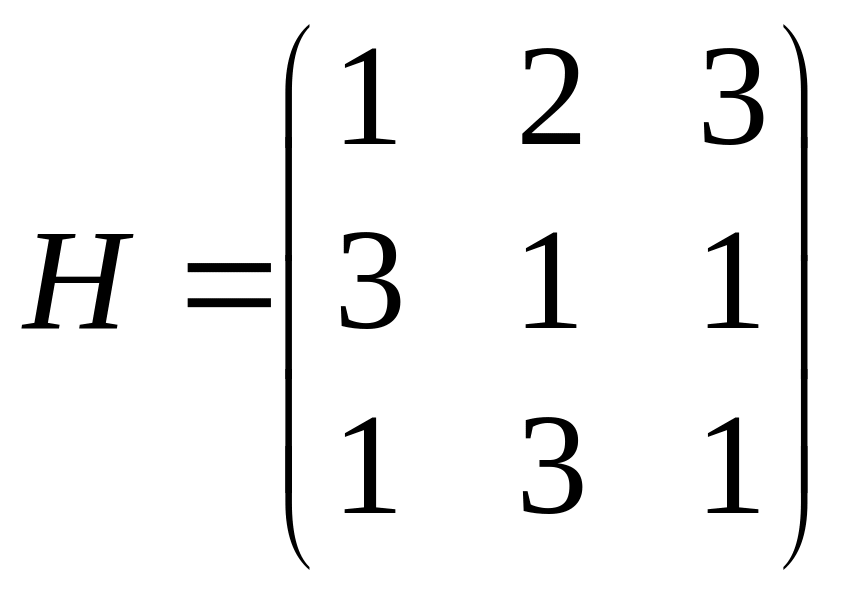
Решение. Матричной игре с данной платежной матрицей будет соответствовать пара двойственных задач линейного программирования:

Найти минимум функции F(Х) = x₁ + x₂ + x₃ при ограничениях:

Найти максимум функции T(Y) = y₁ + y₂ + y₃ при ограничениях:

Здесь

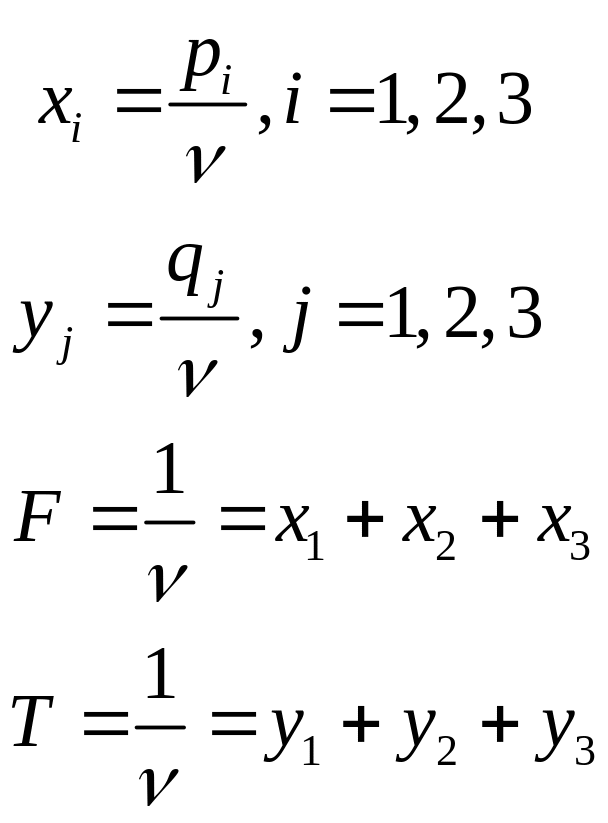
Решаем последнюю задачу симплексным методом.

Базисные перемен- ные								ДО
	1	1	2	3	1	0	0	1
	1	3	1	1	0	1	0
	1	1	3	1	0	0	1	1
	0	-1	-1	-1	0	0	0
		0	5/3		1		0
		1	1/3		0		0	1
	2/3	0	8/3	2/3	0	-1/3	1
		0	-2/3		0		0
	1/4	0	0	9/4	1	-1/8	-5/8
		1	0	1/4	0			1
		0	1	1/4	0			1
		0	0	-1/2	0
		0	0	1
		1	0	0
		0	1	0
		0	0	0

Решение этой задачи

.

Тогда цена игры а вероятности применения стратегий игрока II будут:

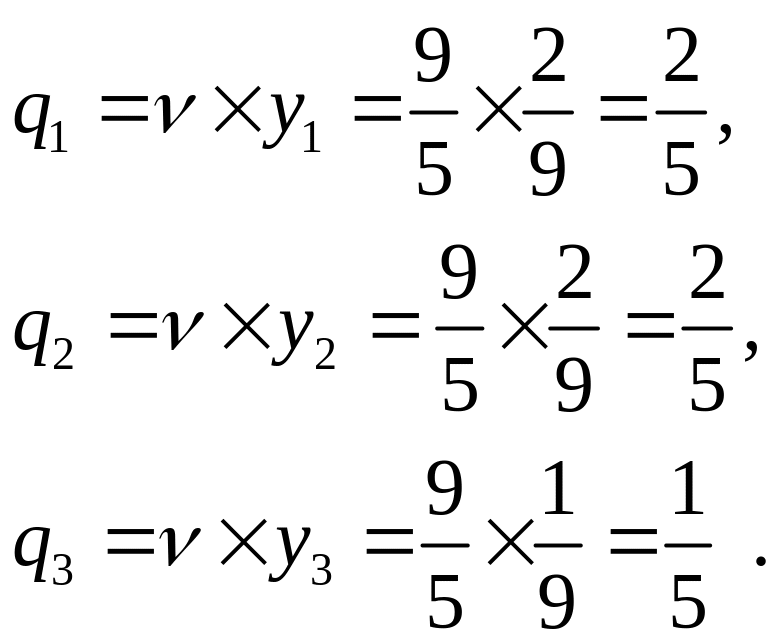
Из симплекс-таблицы находим решение двойственной задачи:

Следовательно, вероятности применения стратегий игрока I:

,

таким образом, оптимальные смешанные стратегии игроков:

, , .