Геометрический метод

Решение игры в смешанных стратегиях допускает наглядную геометрическую интерпретацию. Геометрический метод решения игры включает следующие этапы.

1. В декартовой системе координат по оси абсцисс откладывается отрезок А₁А₂, длина которого равна 1 (рис. 2.1.). Левый конец отрезка точка x = 0 соответствует стратегии A₁, правый, где х = 1,0 — стратегии А₂. Все промежуточные точки этого отрезка соответствуют смешанным стратегиям S₁ = (p₁, p₂).

2. По оси ординат от точки O откладываются выигрыши при стратегии А₁.

3. На линии, параллельной оси ординат, от точки 1 откладываются выигрыши при стратегии А₂ .

Пусть имеется игра с платежной матрицей:

.

Если игрок II применяет стратегию В₁, то выигрыш игрока I при использовании чистых стратегий А₁ и А₂ составляет соответственно a₁₁ = 0,4 и a₂₁ = 0,6. Соединим эти точки прямой В₁В₁ .

Если игрок I при стратегии В₁ применяет смешанную стратегию , то средний выигрыш, определяемый по формуле математического ожидания ₁ = a₁₁p₁ + a₂₁p₂, изображается ординатой точки N на прямой B₁B₁. Прямая B₁B₁ называется стратегией В₁. Ордината любой точки отрезка B₁B₁ равна величине выигрыша игрока I при применении им стратегии A₁ и А₂ с соответствующими вероятностями p₁ и p₂.

Аналогично строим отрезок В₂В₂, соответствующий применению игроком II стратегии В₂ .

Ординаты точек отрезка определяют средний стратегий А₁ и А₂ с соответствующими вероятностями p₁ и p₂ и равных ₂ = a₁₂p₁ + a₂₂p₂.

Пример № 1. Найти оптимальную смешанную стратегию руководителя коммерческого предприятия и гарантированный средний выигрыш при выборе из двух новых технологий продажи товаров и , если известны выигрыши каждого вида продажи по сравнению со старой технологией, которые представлены в виде матрицы игры.

Игрок II Игрок I
	0,4	0,9	0,4
	0,6	0,5	0,5
	0,6	0,9

Решение: находим гарантированный выигрыш определяемый нижней ценой игры которая указывает на максиминную чистую стратегию . Верхняя цена игры что свидетельствует об отсутствии седловой точки, т.к. , тогда цена игры находиться в пределах находим решение игры в смешанных стратегиях геометрическим методам рис. 2.1.

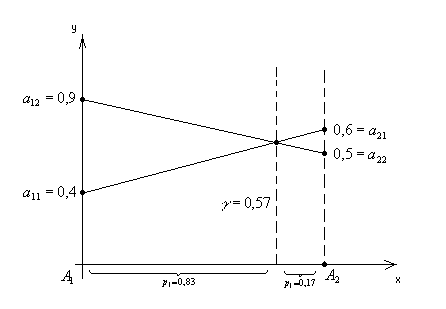
Рис. 2.1. Геометрический метод решения игры

Оптимальная смешанная стратегия и цена игры ровны.

Гарантированный средний выигрыш составляет 0,57.

Исключение доминируемых стратегий

Рассмотрим игру m  n, заданную платежной матрицей:

.

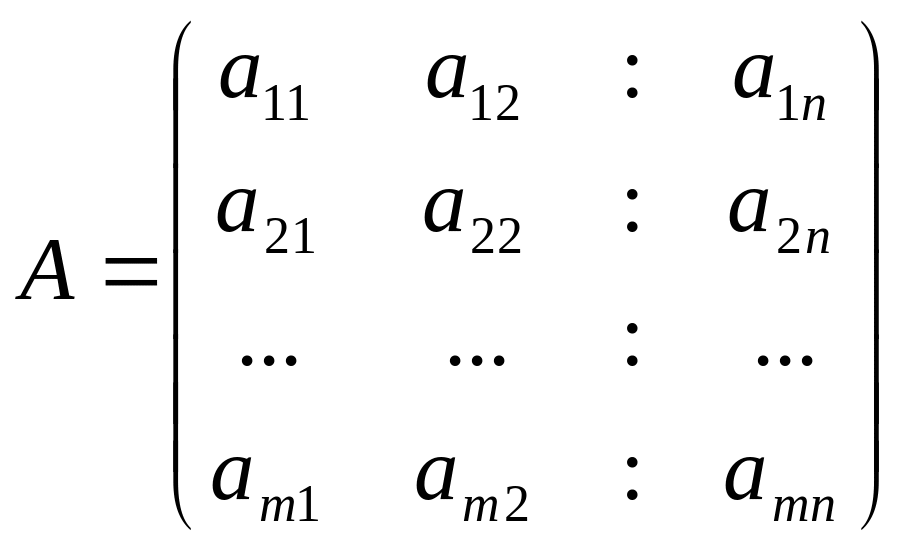При постановке задач, необходимо иметь в виду некоторые преобразования, которые помогают упростить сложную задачу путем изменения – уменьшения размерности платежной матрицы посредством выделения и исключения доминируемых и дублирующих стратегий. Стратегия игрока А_i доминирует над стратегией А_к, если при любом поведении противника даст не меньший выигрыш, а если такой же, то дублирует А_к. В таком случае все элементы i строки больше (доминируют) или равны (дублируют) всех элементов строки k.

Пример. С учетом вариантов конъюнктуры В₁, В₂, В₃, В₄, В₅ сложившейся на рынке и поведения покупателей в микрорайоне города коммерческое предприятие разработало шесть технологий продажи товаров А_1, А_2, А₃, А₄, А₅, А₆. Найти оптимальное решение. Возможные варианты среднедневного товарооборота в млн.руб. приведены в таблице:

	В1	В2	В3	В4	В5
А1	0,4	0,9	0,5	0,5	0,6
А2	0,6	0,5	0,7	0,8	0,9
А3	0,6	0,3	0,8	0,6	0,7
А4	0,3	0,8	0,5	0,4	0,3
А5	0,1	0,3	0,5	0,4	0,3
А6	0,4	0,8	0,5	0,4	0,5

Стратегия А₁ доминирует над стратегией А₆, а стратегия А₄ доминирует над стратегией А₅, следовательно исключаем 5 и 6 строки матрицы

	В1	В2	В3	В4	В5
А1	0,4	0,9	0,5	0,5	0,6
А2	0,6	0,5	0,7	0,8	0,9
А3	0,6	0,3	0,8	0,6	0,7
А4	0,3	0,8	0,5	0,4	0,3

С позиций проигрышей строки В стратегии В_3, В₄ и В₅ доминируют над стратегией В_1, поэтому эти столбцы исключаем из таблицы:

	В1	В2
А1	0,4	0,9
А2	0,6	0,5
А3	0,6	0,3
А4	0,3	0,8

С позиций игрока А стратегия А₁ доминирует над стратегией А₄, а стратегия А₂ доминирует над стратегией А₃, следовательно исключаем 3 и 4 строки матрицы:

	В1	В2
А1	0,4	0,9
А2	0,6	0,5